
Die klassischi Elektrodünamik isch s Däilgebiet vo dr Füsik, wo sich mit bewegte elektrische Laadige und mit elektrische und magnetische Fälder beschäfdigt, wo sich zitlig verändere. D Elektrostatik as Spezialfall vo dr Elektrodünamik beschäftigt sich mit ruende elektrische Laadige und iire Fälder. D Grundchraft vo dr Füsik, wo d Elektrodünamik druf basiert, häisst elektromagnetischi Wäggselwirkig.
D Theorii vo dr klassische Elektrodünamik isch vom Maxwell in dr Middi vom 19. Joorhundert formuliert worde mithilf vo de Maxwell-Gliichige, wo si Naame überchoo häi. D Undersuechig vo de Maxwellgliichige für bewegti Bezuugssüsteem het dr Albert Einstein 1905 zur Formulierig vo dr Spezielle Relatividäätstheorii gfüert. Im Lauf vo de 1940er Joor isch s glunge, d Kwantemechanik und d Elektrodünamik in dr Kwanteelektrodünamik z kombiniere, und deren iiri Vorussaage und d Mässergäbniss wiiche nume minimal von enander ab.
Äi wichdigi Form vo elektromagnetische Fälder sin die elektromagnetische Wälle, wo dr bekanntist Verdräter von ene s sichtbare Liecht isch. Au wenn die füsikalische Grundlaage zum die elektromagnetische Wälle z beschriibe dur d Elektrodünamik gee si, isch iiri Erforschig en äignigs Gebiet vo dr Füsik, d Optik.
Klassischi Elektrodünamik
Grundlegendi Gliichige
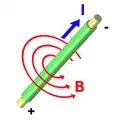 Dr Strom I erzügt im ene Läiter e magnetischs Wirbelfäld .
Dr Strom I erzügt im ene Läiter e magnetischs Wirbelfäld .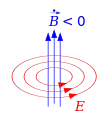 Zitligi Ändrige vom magnetische Fluss füere zum ene elektrische Wirbelfäld .
Zitligi Ändrige vom magnetische Fluss füere zum ene elektrische Wirbelfäld .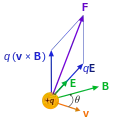 D Lorentzchraft uf e Laadig +q, wo sich mit dr Gschwindigkäit v bewegt.
D Lorentzchraft uf e Laadig +q, wo sich mit dr Gschwindigkäit v bewegt.
S Zämmespiil vo elektromagnetische Fälder und elektrische Laadige wird grundlegend dur die mikroskopische Maxwell-Gliichige
und d Lorentzchraft
bestimmt.
Doodrus chömme mit Hilf vo de Materialgliichige vo dr Elektrodünamik die makroskopische Maxwell-Gliichige. Das si Gliichige für die effektive Fälder, wo in dr Materie ufdräte.
E wichdigi Rolle spiile au:
- d Kontinuitäätsgliichig, , wo säit, ass d Laadig erhalte blibt,
- und dr Satz vom Poynting, wo säit, ass d Energii vo Däili und Fälder im Ganze erhalte blibt.
Potential und Wällegliichig
Die homogene Maxwellgliichige
und
chönne dur d Iifüerig vo de elektromagnetische Potenzial gmääss
und
im ene stärnförmige Gebiet identisch glööst wärde (Poincaré-Lemma). Drbii bezäichnet s sogenannte skalare Potenzial und s Vektorpotenzial. Wil die füsikalische Fälder nume dur Abläitige vo de Potenzial gee si, het mä gwüssi Freihäite und cha d Potenzial ändere und bechunnt drotzdäm die gliiche füsikalische Fälder wider über. Zum Bischbil gäbe und s gliiche -Fäld, wemm mä si dur
mitenander in Beziejig setzt. Wemm mä au no verlangt, ass mä bin ere sonige Dransformazioon s gliiche -Feld überchunnt, muess sich wie
dransformiere. Ere sonige Dransformazioon säit mä Äichdransformazion. In dr Elektrodünamik wärde zwäi Äichige vil verwändet. Die erste isch die sogenannte Coulomb-Äichig oder Straaligsäichig
und die zwäiti d Lorentz-Äichig
- .
D Lorenz-Äichig het dr Vordäil, ass si relativistisch inwariant isch und sich bim ene Wäggsel vo äim Inerzialsüsteem ub en anders strukturell nit änderet. D Coulomb-Äichig isch zwar nit relativistisch inwariant, aber wird eender bi dr kanonische Kwantisierig vo dr Elektrodünamik verwändet.
Setzt mä d - und -Fälder und d Vakuum-Materialgliichige in die inhomogene Maxwellgliichige ii und äicht d Potenzial gmääss dr Lorentzäichig, kopple sich die inhomogene Maxwellgliichige us und d Potenzial erfülle inhomogeni Wällegliichige
Mä bezäichnet do as dr D’Alembertoperator.
D Elektrodünamik und d Relatividäätstheorii
Im Geegesatz zur klassische Mechanik isch d Elektrodünamik nit galilei-inwariant. Das bedütet, wemm mä, wie in dr klassische Mechanik, en absolute, euklidische Ruum und en absoluti Zit annimmt, wo drvo unabhängig isch, denn gälte d Maxwellgliichigen nit in jedem Inerzialsüsteem.
En äifachs Bischbil: Um e gladnigs Däili, wo mit ere konstante Gschwindikäit fliegt, het s en elektrischs und e magnetischs Fäld. E Däili, wo gliich glaade isch und mit dr gliiche Gschwindigkäit fliegt, gspüürt dur s elektrische Fäld vom erste Däili en abstoossendi Chraft, wil sich gliichnaamigi Laadige gegesitig abstoosse; gliichzitig gspüürt s dur s Magnetfäld vom erste Däili en aaziejendi Lorentzchraft, wo d Abstoossig zum Däil kompensiert. Bi Liechtgschwindikäit weer die Kompensazioon vollständig. Im Inerzialsüsteem, wo bäidi Däilu din rueje, git s käi magnetischs Fäld und dorum käi Lorentzchraft. Dört wirkt nume die abstoossendi Coulombchraft, so dass s Däili sterker beschlöinigt wird, als im ursprünglige Bezuugssüsteem, wo sich bäidi Laadige sin beweege. Das widerspricht dr newtonsche Füsik, wil in dere d Beschlöinigung nit vom Bezuugssüsteem abhängt.
Wäge däm her mä zerst aagnoo, ass es in dr Elektrodünamik e bevorzugts Bezuugssüsteem gäb (Äthersüsteem). Mä het aber d Gschwindigkäit vo dr Ärde gegen e Äther nid chönne mässe, wie zum Bischbil bim Michelson-Morley-Experimänt. Dr Hendrik Antoon Lorentz het druf d Äthertheorie modifiziert (Lorentzsche Äthertheorie), aber si ischbald druf vom Albert Einstein mit sinere spezielle Relatividäätstheorii abglööst worde. Dr Einstein het im Newton si absolut Ruum und absoluti Zit dur e vierdimensionali Ruumzit ersetzt. In dr Relatividäätstheorii cunnt am Blatz vo dr Galilei-Inwarianz d Lorentz-Inwarianz, wo vo dr Elektrodünamik erfüllt wird.
In dr manifest Lorentz-forminwariante Beschriibig vo dr Elektrodünamik bilde s skalare Potenzial und s Wektorpotenzial e Viererwektor, analog zum Viererwektor vo Ruum und Zit, so dass d Lorentz-Dransformazioone analog au uf die elektromagnetische Potenzial chönne aagwändet wärde. Bin ere spezielle Lorentz-Dransformazioon mit dr Geschwindigkäit in dr -Richdig gälte für d Fälder im gebrüüchlige SI-Äihäitesüsteem d Dransformazioonsgliichige:
Litratuur
- James Clerk Maxwell: On Physical Lines of Force. In: Philosophical Magazine. 1861–1862.
- John David Jackson: Klassische Elektrodynamik. Walter de Gruyter, Berlin 2006, ISBN 3-11-018970-4.
- Torsten Fließbach: Elektrodynamik. Spektrum Akademischer Verlag.
- Walter Greiner: Klassische Elektrodynamik. 6. Auflage. Harri Deutsch, 2002.
- Wolfgang Demtröder: Experimentalphysik. Bd. 2: Elektrizität und Optik. Springer, Berlin 2006, ISBN 3-540-65196-9.
- Pascal Leuchtmann: Einführung in die elektromagnetische Feldtheorie. Pearson Studium, Münche 2005, ISBN 3-8273-7144-9.
Weblingg
| Dä Artikel basiert uff ere fräie Übersetzig vum Artikel „Elektrodynamik“ vu de dütsche Wikipedia. E Liste vu de Autore un Versione isch do z finde. |