E Differenzialgliichig (vilmol mit DGL oder DG abkürzt) isch e mathematischi Gliichig für e gsuechti Funkzioon vo äinere oder meerere Wariable, wo din au Abläitige vo dere Funkzioon vorchömme. E Hufe Naturgsetz chönne as Differenzialgliichige formuliert wärde. Si sin dorum e wääsentligs Wärkzüüg vo dr mathematische Modellierig und beschriibe, wie sich die verschiidene Gröössene im Bezuug zunenander ändere.
D Analysis undersuecht iiri Löösigstheorii. Für vili Differenzialgliichige git s käi expliziti Daarstellig von ere Löösig, und dorum spiile numerischi Verfaare wo dur Nööcherige Löösige finde, e wääsentligi Rolle.
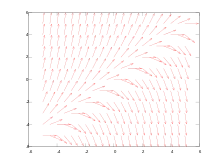
E Differenzialgliichig cha dur e Richdigsfäld aaschaulig gmacht wärde.
Tüpe vo Differenzialgliichige
Mä underschäidet verschiideni Tüpe vo Differenzialgliichige. Ganz grob cha mä si in gwöönligi, parzielli, differentiell-algebraischi, stochastischi, retardierti und integro-differenzielli iidäile.
Gwöönligi Differenzialgliichige
Wenn die gsuechti Funkzioon nume vo äinere Wariable abhängt, so reedet mä von ere gwöönlige Differenzialgliichig. Es chömme nume gwöönligi Abläitige noch dr äinzige Veränderlige vor.
Bischbil:
Wemm mä e gwöönligi Differenzialgliichig für die gsuechti Funkzioon in dr Form
schribt, so säit mä si sig implizit.
Wenn d Differenzialgliichig noch dr höggste Abläitig ufglööst isch, d. h. es gältet
so säit men ere explizit. In de Aawändige isch s äifacher expliziti gwöönligi Differenzialgliichigen mathematisch z verarbäite. Dr höggste Abläitigsordnig , wo vorchunnt, säit mä Ordnig vo dr Differenzialgliichig. Zum Bischbil het en expliziti gwöönligi Differenzialgliichig vo dr 1. Ordnig d Form
Es git en abgschlossnigi Löösigstheorie für expliziti gwöönligi Differenzialgliichige.
Parzielli Differenzialgliichig
Wenn die gsuechti Funkzioon vo meerere Wariable abhängt und wenn s in dr Gliichig parzielli Abläitige noch mer as äinere Wariable git, so reedet mä von ere parzielle Differenzialgliichig. Parzielli Differenzialgliichige si e groosses Fäld und d Theorii isch mathematisch nit abgschlosse. D Forschig beschäfdigt sich zur Zit mit meerere Gebiet.
E Bischbil isch die sogenannti Wermiläitigsgliichig für e Funktion
Mä underschäidet verschiideni Tüpe vo parzielle Differenzialgliichige. Zerst git s lineari parzielli Differenzialgliichige. Bi deene chömme die gsuechti Funkzioon und iiri Abläitige linear in dr Gliichig vor. D Abhängigkäit in Bezuug uf die unabhängige Wariable cha aber durchus nitlinear si. D Theorii vo de lineare parzielle Differenzialgliichige isch am witiste fortgschritte, aber es feelt no vil, bis si abgschlosse isch.
Mä reedet von ere semilineare Gliichig, wenn alli Abläitige vo dr höggste Ordnig linear ufdräte, aber nit d Funkzioon sälber und d Abläitige vo de niidrigere Ordnige. E semilineari Gliichig isch scho schwiiriger z behandle.
Von ere kwasilineare parzielle Differenzialgliichig schwätzt mä, wenn d Koeffiziäntefunkzioone vo de höggste Abläitige zuesätzlig vo niidrigere Abläitige und vo dr umbekannte Funkzioon abhänge. Grad im Gebiet vo de kwasilineare Gliichigen git s zur Zit die mäiste Resultaat.
Wemm mä käi lineari Abhängigkäit in Bezuug uf die höggste Abläitige cha feststelle, säit mä vo dr Gliichig, si sig e nitlineari parzielli Differentialgliichig oder e vollständig-nitlineari parzielli Differenzialgliichig.
Bsundrigs intressant im Gebiet vo de parzielle Differenzialgliichige sin d Gliichige vo dr zwäite Ordnig. In dene Spezialfäll git s no witeri Klassifikazionsmöglikäite.
Aawändige
E Hufe Fenomeen in dr Natur und dr Technik chönne dur Differenzialgliichige und mathematischi Modäll, wo ufe ene ufbaut si, beschriibe wärde. E baar tüpischi Bischbil si:
- Vili füsikalischi Theorie basiere uf Differenzialgliichige: Beweegigsgliichige oder Schwingige in dr klassische Mechanik, s Belasdigsverhalte vo Baudäil, d Elektrodynamik wird vo de Maxwell-Gliichige, d Kwantemechanik vo dr Schrödingergliichig beherrscht.
- in dr Astronomii d Baane vo de Himmelskörper und d Turbulänze im Innere vo dr Sunne,
- in dr Biologii öbbe d Brozäss bim Waggse, bi Ströömige oder in Muskle, oder in dr Ewoluzionstheorii.
- in dr Chemii d Kinetik vo Reakzioone,
- in dr Elektrotechnik wie sich Netzwärk mit Elimänt, wo Energii spiichere, verhalte,
- in dr Differenzialgeometrii s Verhalte vo Flechene,
- in dr Ströömigsmechanik s Verhalte vo Ströömige,
- in dr Ökonomii d Analüse vo wirtschaftlige Waggsdumsbrozäss (Waggsdumstheorii).
- in dr Informatik s Image-Inpainting[1]
S Fäld vo de Differenzialgliichige het d Mathematik aadriibe. In vile Däilgebiet forscht mä hüte an de Existänz-, Äidütigkäits- und Stabilidäätstheorie vo verschidnige Tüpe vo Differenzialgliichige.
Litratuur
- G. H. Golub, J. M. Ortega: Wissenschaftliches Rechnen und Differentialgleichungen. Eine Einführung in die Numerische Mathematik. Heldermann Verlag, Lemgo 1995, ISBN 3-88538-106-0.
- G. Oberholz: Differentialgleichungen für technische Berufe – vierte Auflage. Verlag Anita Oberholz, Gelsenkirchen 1995, ISBN 3-9801902-4-2.
- P.J. Olver Equivalence, Invariants and Symmetry Cambridge Press 1995.
- L. Papula: Mathematik für Ingenieure und Naturwissenschaftler Band 2. Viewegs Fachbücher der Technik, Wiesbaden 2001, ISBN 3-528-94237-1.
- H. Stephani Differential Equations: Their Solution Using Symmetries. Edited by M. MacCallum, Cambridge University Press 1989.
- Benker, H.: "Differentialgleichungen mit MATHCAD und MATLAB", Springer-Verlag Berlin, Heidelberg, New York 2005.
Weblingg
- Matheplanet: Differentialgleichungen – Anleitungen zum Lösen diverser Differentialgleichungen mit Beispielen
- Mathematik-Online Kurs zum Thema Differentialgleichung der Uni Stuttgart
- Prof. Dr. Dörte Haftendorn (Uni Lüneburg) – Differentialgleichungen: Numerik, Beispiele, Isoklinen, …
- Academic Earth – MIT – Differential Equations von Professor Arthur Mattuck
Fuessnoote
- ↑ Peterson, Ivars: Filling in Blanks. In: Science News. 161, Nr. 19, May 11 2002, S. 299–300
| Dä Artikel basiert uff ere fräie Übersetzig vum Artikel „Differentialgleichung“ vu de dütsche Wikipedia. E Liste vu de Autore un Versione isch do z finde. |