
Oobe: D Mässdaate mit em Modäll, wo sich nodinoo aabasst.
Unde: wie sich die normalisierti Summe vo de Kwadraat vo de Feeler entwigglet.
D Usgliichigsrächnig (au Usgliichsrächnig, Usgliichig, Parameterschetzig, Aabassig, Regression oder Fit(ting) gnennt) isch e mathematischi Optimierigsmethode, zum für e Räije vo Mässdaate die umbekannte Parameter vo iirem geometrisch-füsikalische Modäll oder d Parameter von ere Funkzion, wo vorgee isch, z bestimme (z schetze). Im Allgemäine wird si brucht zum überbestimmti Brobleem z lööse.
S Ziil vo dr Usgliichig isch, ass s ändgültige Modäll bzw. d Funkzion am beste zu de Daate und iire chliine Widersprüch, wo umvermiidlig si, basst. Im Allgemäine brucht mä zum Usrächne d Methode vo de chliinste Kwadraat. Bi dere Methode macht mä an de Parameter chliini Verbessrige, so dass d Summe vo de Kwadraat vo alle äinzelne Abwiichige zwüsche de Mässdaate und de Modälldaate so chli wie mööglig wärde. Bi zuefellig verdäilte Feeler im Modäll oder in dr Mässig chunnt mä eso zum woorschiinligste Wärt für die Umbekannte, wo mä will usrächne. Dä chliine Räst, wo no bliibe, säit mä Residue und mit ene cha mä Ussaage mache über d Gnauikäit und Zueverlässigkäit vom Mäss- und Daatemodäll.
Verfaare
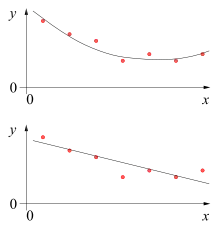
Die mathematische Lösigsverfaare muess mä uf e Modäll basiere, bim grafische Verfaare muess mä käini sonigi Aanaame mache. Do läit mä e stetig krümmti usgliichendi Linie eso, ass si so nooch wie mööglig an de Mässpünggt lit. Je noch däm, was mä über e Hindergrund wäiss, das häisst was mä erwartet, oder wie mä s persönlig bewärtet, wemm mä zum Bischbil äinzelni Mässpünggt as „Usrisser“ aaluegt, cha d Linie allerdings seer underschiidlig usfalle.
Litratuur
- Wolfgang Niemeier: Ausgleichungsrechnung – Statistische Auswertemethoden. 2. Auflage. de Gruyter, Berlin / New York 2008, ISBN 978-3-11-019055-7.
- Helmut Wolf: Ausgleichungsrechnung I und II: Formeln zur praktischen Anwendung. Bonn 1994 (2. Uflaag)
- Mathematische Exkurse: Ausgleichung nach vermittelnden Beobachtungen
- R. Jäger, T. Müller, H. Saler, R. Schwäble: Klassische und robuste Ausgleichungsverfahren – Ein Leitfaden für Ausbildung und Praxis von Geodäten und Geoinformatikern. Wichmann, Heidelberg 2005, ISBN 3-87907-370-8.
Weblingg
- LP – Lineari Usgliichsbrobleem
- Ausgleichungsrechnung oder die Anwendung statistischer Methoden in Vermessungswesen und GIS (Site cha nüme abgrüeft wärde; Suche im Webarchiv) (PDF)
- E Scilab Script für d Usgliichsrächnig vo äidimensionale Mässwärt und Oberfleche mit irgend wele Polynom
- En äifachs Bischbil wie mä d Usgliichsrächnig in dr Geodesii brucht (Matlab-Skript)
- Rekursivi Parameterschetzig am Bischbil vo dr Kräisusgliichig
| Dä Artikel basiert uff ere fräie Übersetzig vum Artikel „Ausgleichungsrechnung“ vu de dütsche Wikipedia. E Liste vu de Autore un Versione isch do z finde. |