Cur-ris
’S e cur-ris an t-obrachadh matamataigeach a chuireas dà àireimh ri chèile gus an t-suim a dhèanamh. ’S e sin an àireamh a tha co-ionnan ris an uimhir gu lèir nuair a chuireas dà uimhir ri chèile.

Tha an t-obrachadh air a sgrìobhadh leis a’ chomharra “+” eadar an dà àireimh a thathar a’ cur-ris, mar eisimpleir:
- 3 + 4.
Faodar seo a leughadh an iomadh dòigh: “cuir-ris trì agus ceithir” no “trì, cuir-ris ceithir” no “cuir ceithir ri trì”. Mar cho-aontar, faodar a leughadh cuideachd gu bheil “a trì ’s a cheithir a’ dèanamh a seachd”:
- 3 + 4 = 7.
Cur-ris nan àireamhan nàdarra
’S e obrachadh àireamhachd as bunaitich a th’ ann an cur-ris. Tha e a’ leantainn fearta ’s bunaitich aig na h-àireamhan nàdarra. ’S e sin gu bheil gach àireamh na h-aon a bharrachd air an tè a th’ ann roimhpe. Mar eisimpleir, nan sgrìobhte “+ 1” an àite “h-aon a bharrachd air”:
- 9 = 8 + 1 = (7 + 1) + 1 = (6 + 1) + 1 + 1 = 5 + 1 + 1 + 1 + 1.
Le bhith a’ dol air ais:
- (1 + 1) + 1 + 1 = (2 + 1) + 1 = 3 + 1 = 4.
Agus nan cuirte 4 an àite “1 + 1 + 1 + 1” sa cho-aontar os cionn, bheireadh seo dhuinn:
- 9 = 5 + 4.
’S e a’ chiall seo gu bheil a naoi na ceithir uiread de “h-aon a bharrachd” air a chòig. Canaidh sinn gu bheil i na ceithir a bharrachd air a chòig.

Tha e a’ leantainn seo gun cuirear dà àireimh nàdarra ri chèile mar seo,
- a + b = c
chionns gum bi àireamh nàdarra ann, can c, a tha b a bharrachd air a (.i. a tha b uiread de h-aon a bharrachd air a). Canaidh sinn cur-ris ris an obrachadh a chuireas dà àireimh ri chèile san dòigh seo.
Co-iomlaideachd cur-ris
’S ann bho na bun-bheachdan sìmplidh os cionn cuideachd a thig am feart cudromach ris an canar co-iomlaideachd. Ma tha àireamh nàdarra air a togail le ath chur-ris na h-àireimh a h-aon, tha e soilleir gu bheil:
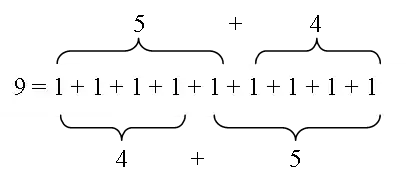
Agus san choitcheannas, ma tha a agus b nan àireamhan nàdarra, gu bheil:
- a + b = b + a.
’S ann ri seo a thathar ag ràdh Lagh Co-iomlaideach Chur-ris, ged tha an “lagh” na thoradh feart cur-ris. Tha obrachaidhean eile ann am matamataig aig nach eil am feart seo agus nach eil a’ cumail ri lagh co-iomlaideach.
Co-thiomsachd cur-ris
’S e obrachadh càraideach a th’ ann an cur-ris. ’S e sin obrachadh dà àireimh, agus dà àireimh a-mhàin. Gus a suas air dà àireimh a chur-ris, bhiodh an treas àireamh air a cur ri suim na dà roimhpe agus gach àireamh eile air a cur ris an t-suim-ruithe:
- (3 + 8) + 2 + 13 + 7 + ...
- = (11 + 2) + 13 + 7 + ...
- = (13 + 13) + 7 + ...
- = (26 + 7) + ...
Ach ma thathar a’ cur-ris sreath àireamhan, chan eil e gu diofar ciamar a thathar gan toirt còmhla nam paidhrichean. Seo feart co-thiomsach chur-ris. Sa riochd as sìmplidh:
- ( a + b ) + c = a + ( b + c )
Mar eisimpleir, ( 3 + 8 ) + 2 = 11 + 2 = 13 = 3 + 10 = 3 + ( 8 + 2 ). Uaireannan thathar ag ràdh Lagh Co-thiomsach Chur-ris no Lagh nan Ceanglaichean Chur-ris ri seo ach, mar a tha an “lagh” co-iomlaideach os cionn, ’s e feart cur-ris a th’ ann.
Neoni agus àireamhan àicheil
’S e neoni an àireamh nach atharraich an dara àireamh ma tha e air a chur rithe. ’S e sin, ma tha
- a + x = a
’s e neoni a th’ ann an x:
- x = 0.
Tha e soilleir gu bheil:
- 0 + a = a + 0 = a
- 0 + 0 = 0
Nise, chionns gu bheil:
- 0 + 1 = 1
...tha e soilleir gu bheil neoni na àireamh air beulaibh na h-aon anns an òrdugh àireamh – ’s e a h-aon a tha “aon a bharrachd” air neoni. Tha àireamhan eile ann a tha ro neoni anns an òrdugh seo. Is iadsan na h-àireamhan àicheil – na h-àireamhan nas lugha na neoni – agus ’s urrainnear an cur-ris anns an aon dòigh:

Mar eisimpleir, ’s e a h-aon a tha ceithir a bharrachd air -3.
- -3 + 4 = 1
Chionns gu bheil cur-ris co-iomlaideach, gabhar a sgrìobhadh cuideachd:
- 4 + -3 = 1
...ach dè tha sin a’ ciallachadh? Gus a h-aon ruigsinn bho cheithir, feumar trì ceuman air ais a ghabhail.
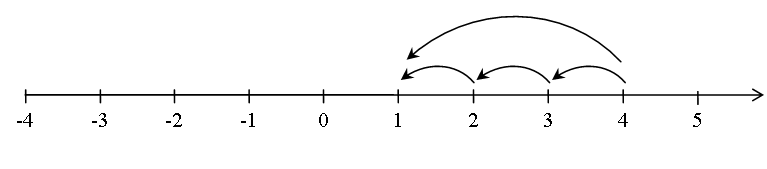
’S e toirt air falbh a tha seo:
- 4 – 3 = 1
’S e toirt air falbh na h-aon rud ri cur-ris àireimh àicheil, ach thoir an aire nach eil toirt air falbh co-iomlaideach mar a tha cur-ris.
- 3 – 4 ≠ 4 – 3.
Cur-ris uimhirean eile
Bloighean
Chan urrainnear dà rud a chur-ris ma tha iad eadar-dhealaichte. Nan cuireadh ceithir ùbhlan agus dà orainsear ri trì ùbhlan agus orainsear, bhiodh seachd ùbhlan agus trì orainsearan ann. ’S urrainnear na h-ùbhlan agus na h-orainsearan a chur-ris fa leth ach chan urrainnear an cur-ris mar-aon. Ach ’s urrainnear mur eil sin a’ cunntadh ùbhlan is orainsearan ach pìosan measa. ’S ann mar seo cuideachd le bloighean:
Gus còigeamhan agus seachdamhan a chur-ris feumar an iomlaid gu bhith nam bloighean den aon sheòrsa. Chionns gu bheil:
- agus
’S urrainnear an cur-ris mar a leanas:
Bheactaran
Bheir an aon bhun-bheachd comas dhuinn bheactaran a chur-ris. Tha cùrsa agus meud aig bheactar, agus ’s docha nach eil e soilleir ciamar a chuireas dà dhiubh ri chèile ma tha cùrsa eadar-dhealaichte aca. Ach ma tha na bheactaran air an cur an cèill a-rèir nan aon bhonn-bheactaran, ’s urrainnear codaichean de bheactaran an cois nam bonn-bheactaran a chur-ris.
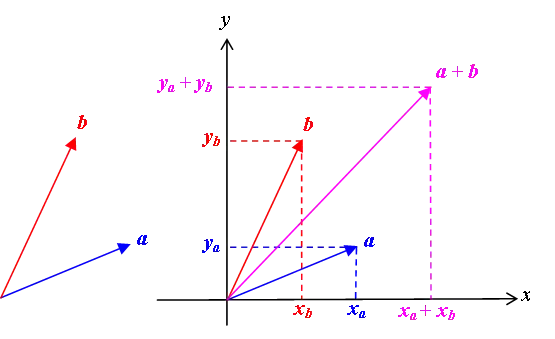
Seo eisimpleir. Biodh agus nam bheactaran ri chur-ris, agus biodh na bonn-bheactaran aca na bheactaran aonadach agus , an cois nan axes x agus y. Biodh xa na chuid-x de bheactar agus ya na chuid-y dheth. Faodaidh sinn a sgrìobhadh an teirmean nam bonn-bheactaran mar a leanas:
Gus an ceartuair, leig an seagh agus leis a’ chomharra “+” an seo, ged a chithear gur h-e cur-ris a th’ ann.
Mar an ceudna:
Faodar a-nis na codaichean-x agus na codaichean-y a chuir-ris, agus nithear ciall de chur-ris bheactaran c = a + b mar a leanas:
Far a bheil:
Gabhar faicinn gum faighear an aon bhuil ma tha an dà bheactar agus air an cur ceann gu ceann. ’S e an t-suim aca am bheactar a tha a’ coileanadh an triantain – am bheactar bho thoiseach gu deireadh .

Anns an aon dòigh, ma tha na codaichean de , an cois na h-axes x agus y, na bheactaran:
...’s e am bheactar na suim:

Meatragsan
Faodar dà mheatraigs a chur-ris le bhith a’ cur-ris na h-eileamaidean co-fhreagarrach fa leth.
Mar eisimpleir:
Ach cha ghabh meatragsan a chur-ris mur eil an dà dhiubh den aon òrdugh (.i. àireamh cholbhan agus shreathan). Tha cur-ris nam meatragsan co-iomlaideach agus co-thiomsach.
Suimeadh
’S e cur-ris sreath (no colbh) àireamhan a th’ ann an suimeadh. Mar eisimpleirean:
Ann am matamataig, tha e gu tric feumail sreath-suimidh a giorrachadh, gu h-àraidh ma tha pàtran aig na teirmean, leis a’ chomharradh Σ (litir mhòr Ghreugais “S” a tha air fuaimneachadh sìghma - σίγμα).
Anns na h-eisimpleirean os cionn, ’s e caochladair brèige a th’ ann an n. Gabhaidh n gach luach mu seach bhon luach ìochdrach gus am fear uachdrach, agus san dòigh seo tha teirmean an t-suimidh air an togail. Tha na luachan seo, aig ìochdar agus aig uachdar na soidhne-suimidh, nan crìochan an t-suimidh. Mar eisimpleir, bhon chiad eisimpleir, tha an suimeadh bho n = 1 gu n = 6:
Anns an dara eisimpleir, gabhaidh n gach luach bho h-aon gu neo-chrìochnachd. Tha e soilleir nach gabhar a sgrìobhadh gach teirm ’s an cur-ris, ach tha ro-innleachdan matamataigeach ann suimidhean neo-chrìochnach mar seo a dh’fhuasgladh, co-dhiù seòrsaichean àraidh dhiubh.