Mengdeliar

Det eegenskap ${\displaystyle \in }$ (as element faan) as det wichtagst ferbinjang tesken mengden. Ales, wat diarütj fulagt, san loogisk slütjer.

${\displaystyle A}$ as en dialmengde faan ${\displaystyle B}$

Gemiansoom mengde faan ${\displaystyle A}$ an ${\displaystyle B}$

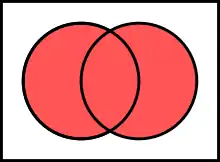
Ferianagt mengde faan ${\displaystyle A}$ an ${\displaystyle B}$

Sümeetrisk diferens faan ${\displaystyle A}$ an ${\displaystyle B}$

Aptäälang

At mengde mä a elementen ${\displaystyle x_{1}}$ bit ${\displaystyle x_{n}}$ häält det element ${\displaystyle a}$ genau do, wan ${\displaystyle a}$ mä ian element ${\displaystyle x_{k}}$ auerianstemet:

${\displaystyle a\in \{x_{1},\dotsc ,x_{n}\}:\Longleftrightarrow a=x_{1}\vee a=x_{2}\vee \dotsb \vee a=x_{n}}$

Det ütjsaag

${\displaystyle a\in \{1,2,3,4\}}$

as likwäärdag (ekwiwalent) mä:

${\displaystyle a=1\vee a=2\vee a=3\vee a=4.}$

Beskriiwang

At mengde faan ${\displaystyle x}$, huarför det eegenskap ${\displaystyle P(x)}$ tudraapt, häält en element ${\displaystyle a}$ genau do, wan det eegenskap üüb ${\displaystyle a}$ tudraapt:

${\displaystyle a\in \{x\mid P(x)\}:\Longleftrightarrow P(a)}$

Uun a ütjsaagenloogik het det:

${\displaystyle \forall x(x\in A\leftrightarrow P(x))}$

Dialmengde

En mengde ${\displaystyle A}$ as en dialmengde faan ${\displaystyle B}$, wan arke element faan ${\displaystyle A}$ uk element faan ${\displaystyle B}$ as:

${\displaystyle A\subseteq B\$ :\Longleftrightarrow \forall x\left(x\in A\,\rightarrow x\in B\right)}

Leesag mengde

En mengde saner elementen as det leesag mengde. Hat woort mä ${\displaystyle \emptyset }$ of uk ${\displaystyle \{\}}$ betiakent.

${\displaystyle A=\emptyset$ :\Longleftrightarrow \forall x(\neg \,x\in A)}

För det jindial ${\displaystyle \neg \,x\in A}$ täält uk: ${\displaystyle x\notin A}$.

Gemiansoom mengde

Diar san ${\displaystyle U}$ mengden. Det gemiansoom mengde faan ${\displaystyle U}$ as det mengde faan objekten, diar uun arke elementmengde faan ${\displaystyle U}$ banen san:

${\displaystyle \bigcap U:=\{x\mid \forall a\in U\colon \;x\in a\}}$

Ferianagt mengde

Det ferianagt mengde faan ${\displaystyle U}$ mengden as det mengde faan objekten, diar uun tumanst ian elemntmengde faan ${\displaystyle U}$ banen san:

${\displaystyle \bigcup U:=\{x\mid \exists a\in U\colon \;x\in a\}}$

Likedenang mengden

Tau mengden san likdenang, wan diar josalew elementen banen san:

${\displaystyle A=B:\Longleftrightarrow \forall x\left(x\in A\,\leftrightarrow x\in B\right)}$

Diferens an komplement

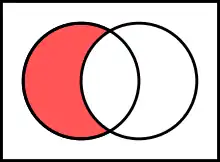${\displaystyle A}$ saner ${\displaystyle B}$

At diferens of uk restmengde faan ${\displaystyle A}$ an ${\displaystyle B}$ ("A saner B") as det mengde faan elementen, diar uun ${\displaystyle A}$, oober ei uun ${\displaystyle B}$ banen san:

${\displaystyle A\setminus B:=\{x\mid \left(x\in A\right)\land \left(x\not \in B\right)\}}$

Det diferens as uk det komplement faan B uun A:

${\displaystyle B^{\complement }:=\{x\mid x\not \in B\}}$

Sümeetrisk diferens

Det as det jindial faan't 'gemiansoom mengde':

${\displaystyle A\triangle B:=\{x\mid \left(x\in A\,\land \,x\not \in B\right)\lor \left(x\in B\,\land \,x\not \in A\right)\}=(A\cup B)\setminus (A\cap B)=(A\setminus B)\cup (B\setminus A)}$

Potensmengde

At potensmengde ${\displaystyle {\mathcal {P}}(A)}$ faan en mengde ${\displaystyle A}$ as det mengde faan aal a 'dialmengden' faan ${\displaystyle A}$.

${\displaystyle {\mathcal {P}}(A):=\{X\mid X\subseteq A\}}$

Karteesisk produkt faan ${\displaystyle A}$ an ${\displaystyle B}$

Karteesisk produkt

At produktmengde faan ${\displaystyle A}$ an ${\displaystyle B}$ as det mengde faan aal a paaren mä det iarst element ütj ${\displaystyle A}$ an det ööder ütj ${\displaystyle B}$:.

${\displaystyle A\times B:=\left\{(a,b)\mid a\in A,b\in B\right\}}$

(1) För dialmengden ${\displaystyle A,B,C\subseteq X}$ täält: Jo san

• refleksiif: ${\displaystyle A\subseteq A}$
• antisümeetrisk: Ütj ${\displaystyle A\subseteq B}$ an ${\displaystyle B\subseteq A}$ fulegt ${\displaystyle A=B}$
• transitiif: Ütj ${\displaystyle A\subseteq B}$ an ${\displaystyle B\subseteq C}$ fulegt ${\displaystyle A\subseteq C}$

(2) A mengdenoperatsioonen ${\displaystyle \cap }$ an ${\displaystyle \cup }$ san komutatiif, asotsiatiif an distributiif:

• Asotsiatiifgesets:
  • ${\displaystyle \left(A\cup B\right)\cup C=A\cup \left(B\cup C\right)}$ an
  • ${\displaystyle \left(A\cap B\right)\cap C=A\cap \left(B\cap C\right)}$
• Komutatiifgesets:
  • ${\displaystyle A\cup B=B\cup A}$ an
  • ${\displaystyle A\cap B=B\cap A}$
• Distributiifgesets:
  • ${\displaystyle A\cup \left(B\cap C\right)=\left(A\cup B\right)\cap \left(A\cup C\right)}$ an
  • ${\displaystyle A\cap \left(B\cup C\right)=\left(A\cap B\right)\cup \left(A\cap C\right)}$
• De Morgan sin gesetsen:
  • ${\displaystyle \left(A\cup B\right)^{\complement }=A^{\complement }\cap B^{\complement }}$ an
  • ${\displaystyle \left(A\cap B\right)^{\complement }=A^{\complement }\cup B^{\complement }}$
• Absorptionsgesets:
  • ${\displaystyle A\cup \left(A\cap B\right)=A}$ an
  • ${\displaystyle A\cap \left(A\cup B\right)=A}$

(3) Gesetsen för diferensmengden:

• Asotsiatiifgesetsen:
  • ${\displaystyle (A\setminus B)\setminus C=A\setminus (B\cup C)}$ an
  • ${\displaystyle A\setminus (B\setminus C)=(A\setminus B)\cup (A\cap C)}$
• Distributiifgesetsen:
  • ${\displaystyle (A\cap B)\setminus C=(A\setminus C)\cap (B\setminus C)}$ an
  • ${\displaystyle (A\cup B)\setminus C=(A\setminus C)\cup (B\setminus C)}$ an
  • ${\displaystyle A\setminus (B\cap C)=(A\setminus B)\cup (A\setminus C)}$ an
  • ${\displaystyle A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C)}$

(4) Gesetsen för sümeetrisk diferensen:

• Asotsiatiifgesets: ${\displaystyle (A\triangle B)\triangle C=A\triangle (B\triangle C)}$
• Komutatiifgesets: ${\displaystyle A\triangle B=B\triangle A}$
• Distributiifgesets: ${\displaystyle (A\triangle B)\cap C=(A\cap C)\triangle (B\cap C)}$
• ${\displaystyle A\triangle \emptyset =A\quad }$an ${\displaystyle A\triangle A=\emptyset }$

Wikibooks: Mengdeliar (sjiisk)
Wikibooks: Bewis uun a mengdeliar (sjiisk)

 Commonskategorii: Mengdeliar – Saamlang faan bilen of filmer

• Ütjsaagenloogik