Virhefunktio
Virhefunktio on eräs useimmin vastaantulevista erikoisfunktioista. Siihen törmää helposti monissa käytännön tilanteissa, varmimmin todennäköisyyslaskennassa ja statistisessa mekaniikassa. Virhefunktio liittyy läheisesti normitetun normaalijakauman kertymäfunktioon. Itse virhefunktion lisäksi usein tulee vastaan myös virhefunktion komplementti.
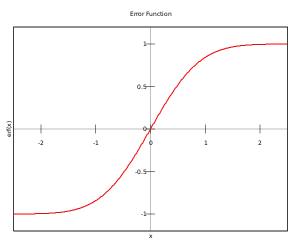
Virhefunktio määritellään integraalina, mutta tarkka esitysmuoto vaihtelee hieman eri lähteissä. Tavallisinlähde? määritelmä on
Virhefunktion ominaisuuksia
Virhefunktio on pariton funktio
ja jos funktion argumentti on kompleksiluku, kompleksikonjugaatille on voimassa
- .
Virhefunktiota ei ole mahdollista lausua alkeisfunktioiden avulla, mutta sitä vastaava Taylorin sarja on
Sille voidaan esittää myös approksimaatio asymptoottisen sarjan avulla. Virhefunktion ensimmäinen derivaatta seuraa välittömästi määritelmästä
ja korkeammat derivaatat voi laskea kaavalla
- ,
missä on :s Hermiten polynomi. Virhefunktiolla on myös integraali
Virhefunktion käänteisfunktio voidaan esittää sarjakehitelmänä
- ,
missä
Virhefunktio ja normaalijakauma
Virhefunktion ja normitetun normaalijakauman kertymäfunktion välillä on yhteys:
- ,
- .
Molempien funktioiden raja-arvo, kun x kasvaa rajatta, on 1, mutta
- ,
kun taas
Muuttujan arvolla x=0 saa virhefunktio arvon 0 mutta normaalijakauman kertymäfunktio arvon 1/2.
Virhefunktion komplementti
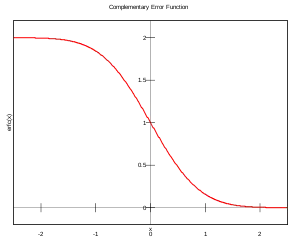
Virhefunktion komplementti määritellään
tai yhtäpitävästi integraalina
- .
ja se toteuttaa differentiaaliyhtälön
- .
Virhefunktion komplementin derivointikaava muistuttaa virhefunktion vastaavaa
ja integraalikin muistuttaa virhefunktion integraalia
Aiheesta muualla
- Virhefunktio Mathworldissa (englanniksi)
- Virhefunktion komplementti Mathworldissa (englanniksi)