Venturi-ilmiö
Venturi-ilmiö on Bernoullin lakiin liittyvä ilmiö, jossa virtaavan fluidin nopeus suurenee ja paine pienenee, kun se kulkee kavennetun putken läpi.[2] Koska aineen tilavuusvirtausnopeuden (yksikkö m3/s) on pysyttävä vakiona, niin putken kaventuessa on virtausnopeuden (yksikkö m/s) suurennuttava, mikä johtuu jatkuvuusyhtälön toteutumisesta. Ja kun virtaavan fluidin nopeus kasvaa putken kaventuessa, on fluidin aiheuttaman paineen pienennyttävä.[1][3]
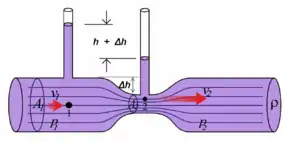
Venturi-ilmiö on nimetty italialaisen fyysikon Giovanni Battista Venturin mukaisesti.[3]
Yhtälöitä
Bernoullin yhtälö
Bernoullin yhtälö putkessa virtaavalle aineelle, jonka tiheys on vakio (aine siis on kokoonpuristumaton) ja gravitaation aiheuttama kiihtyvyys , voidaan esittää muodossa [1]
- ,
missä putken pisteessä 1 putken korkeus on ja aineen paine on . Vastaavasti putken pisteessä 2 putken korkeus on ja aineen paine on .
Paine-ero putken eri kohdissa
Jos kuitenkin tarkastellaan tilannetta, jossa putkella ei ole korkeuseroja (eli = ), niin Bernoullin yhtälöstä jätetään huomioimatta termit . Tällöin voidaan laskea putken pisteissä 1 ja 2 kulkevan aineen paineiden erot muokatulla Bernoullin yhtälöllä
- ,
joka siis kuvaa putkea, jossa pisteessä 2 putki on ohuempi kuin pisteessä 1.
Tilavuusvirta
Tilavuusvirta kertoo, kuinka suuri tilavuus virtaavaa ainetta putken tietyn kohdan poikkileikkauksen läpi kulkee aikayksikköä kohden. Jatkuvuusyhtälön mukaisesti tilavuusvirta on kokoonpuristumattomalle fluidille putken paksuudesta riippumatta vakio
- ,
missä siis on putken kohdan 1 poikkileikkauksen pinta-ala ja on putken kohdan 2 poikkileikkauksen pinta-ala. Tämä yhtälö yhdistettynä yllä olevaan paine-eroyhtälöön
voidaan laskea putkessa virtaavan aineen tilavuusvirta yhtälöllä
- .
Esimerkkejä Venturi-ilmiöstä
- Kaasutin
- Muita suonia ohuemmat hiussuonet ihmisen verenkierrossa
- Kaupungeissa ilmamassojen pakotettu liikkuminen tuulen mukana suurten rakennusten välissä
- Vesiputkistoissa olevan veden alipaineistus vesihanan avulla
- Suihke- ja sumutinpullot (esimerkiksi hajuvesi ja spraymaali)
- Vaahtosammutin
Lähteet
- Young & Freedman: ”14.5”, University Physics with Modern Physics, 11. painos. Pearson, 2004. ISBN 0-321-20469-7. (englanniksi)
- The Language of Physics - Venturi effect 123exp-science.com. (englanniksi)[vanhentunut linkki]
- G. Rozza, D. B. P. Huynh & NC Nguyen: Venturi: Potential Flow (pdf) augustine.mit.edu. 28.3.2008. Arkistoitu 31.10.2008. (englanniksi)
Aiheesta muualla
- Venturi Tube Simulation. (englanniksi)