Uomaluokittelu

Uomaverkostoja voi tutkia matemaattisesti graafiteorian (topologia) keinoin. Uomista voidaan muodostaa esimerkiksi puurakenne, jossa solmut ovat uomien yhtymiskohtia ja uomat ovat solmuja yhdistävät kaaria. Jos rajoitutaan vain kahden uoman yhtymiseen kussakin solmussa, saadaan yksinkertainen binääripuu, joka on helppo tietorakenne GIS-sovelluksien pohjaksi. Todellisia uomaverkostoja ei aina voi esittää binääripuulla, sillä esimerkiksi bifurkaatiot (uomien haarautuminen erilleen, suistohaarat) ja tulvauomien rakentaminen jokien alajuoksuille ei voi niillä mallintaa. Siksi yleisemmät graafit ovat mallinnuksissa hyödyllisempiä tietorakenteita.[1][2]

Geomorfologiassa topologinen luokittelu antaa luokittelunumeron 1 uomaverkoston joensuun uomalle. Seuraavat ylävirran puolella sijaitsevat tähän yhtyvät uomat saavat numerot 2. Jokainen yhtymiskohta muodostuu ylävirran uomista, joiden numero on yksi suurempi kuin niiden yhtynyt uoma alempana. Uomaverkoston latvahaaroilla on siten suurimmat luokittelunumerot ja verkoston suurinumeroisin uoma kertoo, kuinka monta ”binääripuun oksaa” verkoston pisimpää reittiin kuuluu.[1][2]

Perinetinen uomaluokittelu hakee lähtökohdaksi ensin uomaverkoston pääuoman, jonka se numeroi luokkaan 1.

Perinteinen uomaluokittelun [lower-alpha 2] (engl. classical stream order, Hack's stream order tai Gravelius' stream order, saks. klassische flussordnung) johtoajatus oli etsiä uomaverkostolle ”vesitie” eli pääuoma. Pääuoman kriteeri oli yleensä jokin seuraavista: se oli vesimäärältään suurin uoma, se oli uomaverkoston pisin uoma tai se oli samanniminen joensuusta latvoille saakka. Pääuoman luokittelunumero oli 1. Sen merkitseminen aloitettiin pääuoman joensuusta, missä se laski järveen tai mereen. Sitten noustiin yläjuoksulle päin ja jokaisessa uomien yhtymäkohdassa päätettiin kumpi uoma oli kriteerin mukaan pääuoma ja kumpi sivu-uoma. Pääuomalle annetiin luokittelunumeroksi 1 ja sivu-uomalle numero 2. Pääuomaa etsittiin tällä tavalla viimeiseen latvahaaraan saakka. Kaikki sivu-uomat, joiden luokittelunumero oli 2, käytiin samalla tavalla läpi. Numero 2 tuli antaa sivu-uoman ”pääuomalle” aina sen latvahaaraan asti. Tähän yhtyneet sivu-uomat merkittiin numerolla 3. Vastaavaa luokittelua toistetiin myös sivu-uomille 3, 4 ja niin edelleen, kunnes koko uomaverkosto oli luokiteltu. Perinteisellä luokituksella ei ole enää käytännön merkitystä, sillä sen ovat korvanneet muut luokittelimenetelmät.[2]

Horton-luokittelu [3] (engl. Horton's stream order [1]) oli insinööri ja maaperätieteilijä Robert Hortonin (1875–1945 [lower-alpha 3]) kehittämä ja vuonna 1945 julkaisema tapa luokitella jokien uomaverkoston pääuomat ja sivu-uomat lähinnä hydrologian tarpeisiin. Hänen menetelmänsä oli ainoastaan kääntää perinteisen eli Hackin uomaluokkittelun numerointia niin, että pääuoma sai suurimman numeron ja latvahaarat numeron 1. Hänen luokittelussa uomaverkoston pääuomalla oli sama numero joensuusta viimeiseen latvahaaraan asti.[1]

Horton-luokittelun käyttämisen vaikeus tulee esille niissä päätöksissä, joissa yhtymäkohdan uomat jaetaan pääuomaksi ja sivu-uomiksi. Siihen ei ole olemassa matemaattista tapaa, vaan siinä on tunnettava joen uomien suuruudet. Yleisin kriteeri on tarkastella uoman virtaamia tai muita helposti mitattavia uoman suuruuteen viittaavia ominaisuuksia. Pääsääntö on, että yhtymäkohtaan tuleva suurempi uoma valitaan aina pääuomaksi. Tietokoneelle ei ole voitu opettaa luonnollista tapaa suoritta Horton-luokittelu uomaverkon geometrian perusteella. Sitä voidaan kuitenkin yrittää luokittelemalla uomaverkosto ensin Strahler-luokittelulla ja muuttamalla se sitten Horton-luokittelua vastaavaksi noudattamalla tiettyjä muunnossääntöjä. Horton-luokittelulla ei ole enää käyttöä nykyaikaisessa hyrdologisessa työskentelyssä ja sen merkitys on lähinnä historiallinen.[1]

Uomaverkon Strahler-luokitus on sen suurin luokkanumero eli 3.

Kuvitteellisen uomaverkoston Strahler-numerointi:
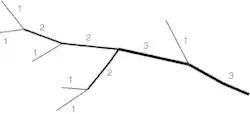
1. latvauomat
2. uomat, johon latvauomat yhtyvät
3. uomat, johon 2. luokan uomat yhtyvät
4. uoma, johon 3. luokan uomat yhtyvät
Uomaverkoston 4. luokan uoma on valuma-alueen pääuoma, joka laskee esimerkiksi mereen.

Strahler-luokittelu [3] (engl. Strahler's stream order [1]) oli Arthur Strahlerin (1918–2002) vuonna 1945 esittämä luokittelumenetelmä, jossa oli huomioitu joitakin Hortonin luokittelussa esiintyviä epäkohtia. Se laaditaan siten, että merkitään aluksi kaikki uomaverkoston latvapurot luokittelunumerolla 1. Sitten edetään alajuoksulle päin ja aina kun kaksi 1. luokan uomaa yhtyvät, annetaan jatkouomalle luokittelunumeroksi 2. Jatkossakin kahden saman luokan uoman yhtyminen kasvattaa jatkouoman luokitusta yhdellä. Kahden eriluokkaisen uoman yhtyminen ei kasvata luokkanumeroa, vaan jatkouoma jatkaa suuremman luokan luokittelunumerolla. Esimerkiksi silloin, kun 1. luokan ja 3. luokan uomat yhtyvät, tulee jatkouoman luokaksi edelleen 3. luokka.[1]

Strahler-luokituksella on se etu, että se on matemaattisesti hyvin määritelty. Kunkin uoman luokka määräytyy sekä sen asemasta muihin uomiin nähden että sen sijaintiin latvavesien puroihin nähden. Tutkimalla esimerkiksi karttaa, voi kuka tahansa, ja erityisesti myös tietokone, luokitella uomaverkoston uomat. Valitsemalla luokittellun uomaverkoston mikä tahansa yhtymäkohta, kertoo sen luokkanumero kuinka pitkä on yläjuoksulla oleva uomaverkon osan puurakenne. Uomien luokkanumerot korreloivat esimerkiksi uoman pituuden, uomien lukumäärän ja uoman kaltevuuden kanssa [3][4]. Luokittelun epäkohta on sen riippuvuus kartan mittakaavasta. Jos latva-alueen pienimmät purot on merkitty huonosti, tulee eri karttoja käyttäville luokittelijoille erilaiset luokittelunumerot. Strahler-luokitus on herkkä sille, että 1. luokan uomat eivät ole samankaltaisia. Esimerkiksi uomissa tulisi olla jatkuvasti vettä, jotta niiden vaikutukset alajuoksulla olisivat samat. On myös huomattu, että uoman luokkanumero ei aina vastaa uoman hydrologisia ja sen ekologisia ominaisuuksia, vaikka se korreloi hyvin uomien ulkoisien ominaisuuksien kanssa [5].[1][3]

Shreve-luokittelussa aloitetaan latvahaaroista, joille annetaan numeroksi 1. Kaksi 1. luokan haaraa yhtyvät 2. luokan haaraksi. Viimeinen uoma saa luokkanumeroksi 6, sillä se muodostuu 5.- ja 1. luokan uomista.

Shreve-luokittelu [lower-alpha 2] (engl. Shreve's stream magnitude [1]) perustui Shreven vuonna 1967 julkaisemaan tapaan huomioida esimerkiksi uomiin kertyvää vettä laskemalla yläjuoksulta tulevien uomien luokat yhteen. Jos siis kaksi 1. luokan uomaa yhtyvät, jatkaa alavirtaan 2. luokan uoma. Jos 3. luokan uoma yhtyy 5. luokan uoman kanssa, jatkaa alaspäin 8. luokan uoma. Näin ajatellen uomille annettavat luokittelunumerot eivät enää kuvaakkaan luokkia vaan ne ilmaisevat uomien summatiivisia ominaisuuksia, jotka se perii molemmilta yläjuoksulta yhtyviltä uomilta (eli kuin määrän mitta tai painokerroin, engl. magnitude). Eräs tulkinta olisi, että esimerkiksi veden määrä, virtaama ja saasteiden määrä kasvaa additiivisesti uomien yhtyessä. Uomien numerointi aloitetaan latvavesistä antamalla niille luokkanumeron 1. Silloin saadaan kuvan mukainen luokittelu.[1][6][7]

Scheidegger-luokittelu [lower-alpha 2] (engl. Scheidegger's stream magnitude [1]) oli samanlainen kuin Shreve-luokittelu paitsi, että latvavesien uomille annetaan luokittelussa numero 2. Scheidegger-luokittelu saadaan, kun ensin tehdään Shreve-luokittelu ja sitten kerrotaan kaikki luokittelunumerot kahdella.[1][7]

• Horton, R. E.: Erosional developments of streams and their drainage basins; hydrophysical approach to quantitative morphology. Geological Society of America Bulletin, 1945, nro 56, s. 275–370. USA: (englanniksi)

• Strahler, A. N.: Quantitative analysis of watershed geomorphology. Transactions, 1957, nro 38, s. 913–920. American Geophysical Union. (englanniksi)

• Shreve, R. L.: Statistical Law of Stream Numbers. Journal of Geology, 1966, 74. vsk, s. 17-37. (englanniksi)

• Karvonen, Tuomo & Warsta, Lassi: Hydrologisten mallien pilvipalvelu, Suomessa kirjataan näkyviin Strahlerin numero, 5.12.2019
• Briney, Amanda: What is stream order?
• Hierarchies in trees gitta.info. GITTA. Viitattu 28.1.2020. (englanniksi)