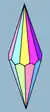
Trapetsoedri

n-kulmainen trapetsoedri, antidipyramidi, antibipyramidi eli deltoedri on avaruusgeometriassa n-kulmaisen antiprisman duaalikappale.[2] Symmetrisimmillä trapetsoedreilla on tahkoinaan 2n keskenään yhtenevää leijaa, joita sanotaan myös trapetseiksi eli deltoideiksi. Tahkot sijaitsevat symmetrisesti kappaleen akselin ympärillä.

Trapetsoedrit

Conwayn merkintä	dA_n
Schläflin symboli	{ } ⨁ {n}[1]
Coxeterin diagrammit
Tahkoja	2n leijaa
Särmiä	4n
Kärkiä	2n + 2
Tahkokonfiguraatio	V3.3.3.n
Symmetriaryhmä	D_nd, [2⁺,2n], (2*n), kertalukua 4n
Rotaatioryhmä	D_n, [2,n]⁺, (22n), kertalukua 2n
Duaalikappale	antiprisma
Ominaisuudet	kupera, tahkotransitiivinen

Luku n, jonka mukaan trapetsoeria nimitetään n-kulmaiseksi, ei tarkoita, että tahkot olisivat n-kulmioita, sillä ne ovat aina nelikulmioita. Sen sijaan luku viittaa kärkien sijoittumiseen kappaleen symmetria-akselin ympärillä. Sen sijaan n-kulmaisella antiprismalla todella on tahkoina kaksi n-kulmiota.

n-kulmainen trapetsoedri voidaan jakaa kahdeksi yhteneväksi n-kulmaiseksi pyramidiksi sekä yhdeksi n-kulmaiseksi antiprismaksi.

Nimi

Trapetsoedreja sanotaan joskus myös deltoedreiksi- Ne ovat kuitenkin aivan eri asia kuin deltaedrit, joiden sivut ovat tasasivuisia kolmioita.

Kristallografiassa trapetsoedrilla tarkoitetaan usein 24-tahkoista monitahokasta, jonka tahkot ovat epäsäännöllisiä nelikulmioita. Tämä monitahokas tunnetaan myös nimellä deltoidinen ikositetraedri, leukitoedri tai tetragonaalinen trisoktaedri.[3]

Tahkot, kärjet ja särmät

Symmetrisellä n-trapetsoedrilla on 2n tahkoa, jotka kaikki ovat muodoltaan yhteneviä leijoja, erikoistapauksessa neliöitä.

n-trapetsoedrilla on 2n + 2 kärkeä. Niistä kaksi on huippuja, joissa kohtaa toisensa n tahkoa ja yhtä monta särmää, kun taas kaikissa muissa kohtaavat toisensa kolme tahkoa ja kolme särmää.

Särmiä n-trapetsoedrilla on 4n. Kumpaankin huippuun johtaa n särmää, kun taas loput 2n särmää yhdistävät trapetsoedrin muut kärjet toisiinsa.

Myös kuutio voidaan käsittää trapetsoedrin erikoistapaukseksi, 3-trapetsoedriksi, jonka tahkot ovat neliöitä. Se on oktaedrin duaalikappale, ja oktaedri on samalla antiprisma.[2]

Symmetria

Symmetrisimmän n-kulmaisen trapetsoedrin symmetriaryhmä on D_nd, kertalukua 4n, paitsi kuution tapauksessa, jolla on laajempi symmetriaryhmä O_d, kertalukua 48, jolla on aliryhminään neljä versiota ryhmästä D_3d.

Trapetsoedrin rotaatioryhmä on D_n, kertalukua 2n, paitsi kuution tapauksessa, jolla on laajempi rotaatioryhmä O, kertalukua 24, jolla on aliryhminään neljä versiota ryhmästä D₃.

Jos trapetsoedrin tahkoina olevat leijat korvataan sellaisilla keskenään yhtenevillä nelikulmioilla, joissa vain kaksi sivuista on yhtä pitkiä, saadaan väännetty trapetsoedri. Sen symmetria on D_h. Rajatapauksessa jokaisen nelikulmion sivuista yhden pituus menee nollaksi, jolloin kappale muuttuu bipyramidiksi.

Jos vastakkaisia huippuja ympäröivät leijat ovat eri muotoisia, kappaleella on vain symmetria C_nv, kertalukua 2n. Kappaletta sanotaan tällöin asymmetriseksi trapetsoedriksi. Sellaisen duaali on asymmetrinen antiprisma, jonka ylä- ja alapuolen monikulmioilla on eri pituiset säteet. Jos se vielä väännetään, sen symmetria supistuu sykliseksi symmetriaksi C_n kertalukua n.

Esimerkkejä muunnelmista
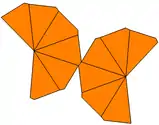
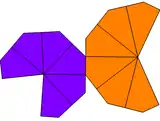
Tyyppi	Väännetty trapetsoedri	Asymmetrinen trapetsoedri	Asymmetrinen ja väännetty trapetsoedri
Symmetria	D_n, (nn2), [n,2]⁺	C_nv, (*nn), [n]	C_n, (nn), [n]⁺
Kuva (n=6)
Verkko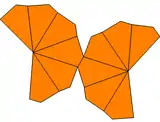

Muodot

n-trapetsoedrillä on 2n nelikulmaista tahkoa ja 2n+2 kärkeä. Kärjistä kaksi on polaarisella akselilla, muut sijaitsevat kahdella eri tasolla olevan säännöllisen n-kulmion kärjissä.

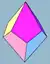
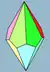
Trapetsoedrit V.n.3.3.3
Pohjana monitahokas
Pallopinnan laatoitukset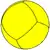
Konfiguraatio	V2.3.3.3	V3.3.3.3	V4.3.3.3	V5.3.3.3	V6.3.3.3	V7.3.3.3	V8.3.3.3	...V10.3.3.3	...V12.3.3.3	...V∞.3.3.3

Erikoistapauksia:

n=2: Degeneroitunut muoto, muodostaa geometrisen tetraedrin, jolla on 6 kärkeä, 8 särmää ja tahkoina 4 kolmiota. Näiden kolmioiden voidaan ajatella syntyneen siten, että leijan kaksi vierekkäistä, yhtä suurta sivua ovat samalla suoralla. Tämän duaalikappale on antiprisman degeneroitunut muoto, joka sekin on tetraedri.
n=3: Kyseessä on kolmikulmaisen antiprisman duaalikappale, jonka tahkot ovat neljäkkäitä tai neliöitä, minkä vuoksi nämä trapetsoedrit ovat samalla zonoedreja. Niitä sanotaan romboedreiksi. Ne ovat ikään kuin kuutioita, joita mahdollisesti on venytetty yhden avaruuslävistäjänsä suunnassa. Samalla ne ovat suuntaissärmiöitä, joilla on yhtenevät neljäkkään muotoiset tahkot.
60°:n romboedri rhombohedron, joka on sen leikkavilla tasoilla jaettu keskellä olevaksi säännölliseksi oktaedriksi ja kahdeksi säännölliseksi tetraedriksi.
- Romboedristä on olemassa sellainen erikoistapaus, jossa sen tahkojen kulmat ovat 60° ja 120°. Tällainen romboedri voidaan jakaa kahdeksi säännölliseksi tetraedriksi ja säännölliseksi oktaedriksi. Koska suuntaissärmiöillä voidaan täyttää tila, voidaan samoin tehdä myös yhdistelmällä tetraedreja ja oktaedreja, vaikka tilaa ei voidakaan täyttää pelkillä tetraedreilla eikä pelkillä oktaedreilla.

Sovelluksia

Eräissä kidehiloissa atomit ovat sijoittuneet tilaan sillä tavoin, että ne muodostavat kolmikulmaisia tai kuusikulmaisia trapetsoedrin muotoisia soluja.[4]
Viisikulmainen trapetsoedri on ainoa Platonin kappaleisiin kuulumaton monitahokas, jota yleisesti käytetään arpanoppana, pääasiassa eräissä roolipeleissä kuten Dungeons & Dragons. Koska sillä on 10 tahkoa, sitä toistuvasti heittämällä voidaan valita satunnaisesti desimaaliluku, jossa on haluttu määrä desimaaleja. Tyypillisesti käytetään kahta eriväristä noppaa, joilla saadaan valituksi satunnaisesti jokin kokonaisluvuista väliltä 00 .. 99.

Tähtitrapetsoedrit

On olemassa myös itsensä leikkaavia trapetsoedrejä, joiden keskuskuviona on tähtimonitahokas. Ne määritellään leijan muotoisten tahkojen avulla, jotka yhdistävät monikulmion sivut kahteen annettuun pisteeseen. Tähtitrapetsoedreja merkitään murtoluvuilla samaan tapaan kuin tähtimonikulmioitakin, ja p/q-trapetsoedrin Coxeterin diagrammi on .

Uniformiset duaaliset p/q -tähtitrapetsoedrit arvoon p = 12 saakka
5/2	5/3	7/2	7/3	7/4	8/3	8/5	9/2	9/4

10/3	11/2	11/3	11/4	11/5	11/6	11/7	12/5	12/7

Lähteet

Anthony Pugh: ”Chapter 4: Duals of the Archimedean polyhedra, prisma and antiprisms”, Polyhedra: A visual approach. Berkeley, Kalifornia: University of California Press. ISBN 0-520-03056-7.

Viitteet

Norman Johnson: ”Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c”, Geometries and Transformations. Cambridge University Press, 2018. ISBN 978-1-107-10340-5. (englanniksi)
Trapezohedron Wolfram MathWorld. Eric W. Weisstein. Viitattu 12.2.2019. (englanniksi)
Daniel N. Lapedes: ”Trapezohedron”, Dictionary of Physics and Mathematics. McGraw–Hill, 1978. ISBN 0-07-045480-9. (englanniksi)
Promorphology of Chrystals, II: Trigonal-trapezohedric Class, 3 2 ja Hexagonal-trapezohedric Class, 6 2 2 metafysica.nl. Viitattu 12.2.2019. (englanniksi)

Katso myös

Bipyramidi

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Norman Johnson: ”Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c”, Geometries and Transformations. Cambridge University Press, 2018. ISBN 978-1-107-10340-5. (englanniksi)

[Wolfram-2] Trapezohedron Wolfram MathWorld. Eric W. Weisstein. Viitattu 12.2.2019. (englanniksi)

[3] Daniel N. Lapedes: ”Trapezohedron”, Dictionary of Physics and Mathematics. McGraw–Hill, 1978. ISBN 0-07-045480-9. (englanniksi)

[4] Promorphology of Chrystals, II: Trigonal-trapezohedric Class, 3 2 ja Hexagonal-trapezohedric Class, 6 2 2 metafysica.nl. Viitattu 12.2.2019. (englanniksi)