Titiuksen–Boden laki

Titiuksen–Boden laki on matemaattinen sääntö, jonka avulla voi arvioida planeettojen etäisyydet. Lain mukaan Merkurius on 0,4; Venus 0,7; Maa 1,0; Mars 1,6 jne. AU:n etäisyydellä Auringosta. Laki huomattiin 1700-luvulla. Oletetaan, että Titius-Boden laki (Boden laki, T-B laki, TB laki) on syntynyt planeettojen toisiinsa aiheuttamien häiriöiden ja/tai aurinkokunnan syntyvaiheessa tapahtuneiden planeettojen ja kaasu-/planetesimaalikiekon välisen vuorovaikutuksen ansiosta. Tuolloin planeetat vaeltelivat pääasiassa sisäänpäin, mutta myös ulospäin niin sanotun migraatioteorian mukaan. Titiuksen–Boden lakiin liittyy monia kiertoaikojan välisiä resonansseja muun muassa Saturnuksen ja Uranuksen välillä.

Kaava

Alkuperäinen kaava Titiuksen–Boden laille on:

a={\frac {n+4}{10}}

jossa n = 0, 3, 6, 12, 24, 48 ..., jokainen n:n arvo kaksi kertaa edellinen, kantaluku on 3.

Nykyaikainen Titiuksen–Boden lain muotoilu on:

a=0{,}4+0{,}3\times k

Missä k=0, 1, 2, 4, 8, 16, 32, 64, 128 (0 ja luvun 2 potenssit)

Karkea muotoilu laille on: seuraavan planeetan etäisyys Auringosta on suunnilleen kaksi kertaa niin suuri kuin edellisen planeetan etäisyys Auringosta. Esimerkiksi Saturnuksen etäisyys on kaksi kertaa Jupiterin etäisyys.

Titiuksen–Boden laki ja käytäntö

Planeetta	k	Titius-boden etäisyys	Todellinen etäisyys
Merkurius	0	0,4	0,39
Venus	1	0,7	0,72
Maa	2	1,0	1,00
Mars	4	1,6	1,52
asteroidit	8	2,8	2,77
Jupiter	16	5,2	5,20
Saturnus	32	10,0	9,54
Uranus	64	19,6	19,2
Neptunus	-	-	30,1
plutinot	128	38,8	39,5[1][2]

Asteroidivyöhykkeellä ei ole suurta planeettaa. Kääpiöplaneetta Ceres etäisyydellä 2,77 AU eli Titiuksen–Boden laissa k=8 on vain yksi miljoonista, tosin suurin.[3] Cerestä pidettiin aluksi planeettana, mutta kun yhä lisää kappaleita löytyi samalta alueelta niitä ruvettiin sanomaan asteroideiksi tai pikkuplaneetoiksi. Ceres luokiteltiin myöhemmin kääpiöplaneetaksi. [4][5] Neptunus muodostaa selvän poikkeuksen säännöstä, sillä se sattuu kohtien k=64 ja k=128 välille. Sitä vastoin Pluto sijaitsee suunnilleen Titius-Boden lain mukaisella kohdalla, mutta nykyisin Kuiperin vyöhykkeen löytöjen vuoksi sitä ei enää luokitella planeetaksi vaan kääpiöplaneetaksi (kuten Ceres sekin on vain yksi monista).[6] Pluton lisäksi muitakin kappaleita on löydetty Neptunuksen kiertoajan 2:3 resonanssista eli etäisyydeltä, jolla kiertoaika on 2:3 Neptunuksen kiertoajasta.[2]

Titiuksen–Boden laki Merkuriuksen yksiköissä

Merkurius on Aurinkoa lähin planeetta. Sen etäisyyttä voidaan merkitä lyhenteellä MU. Kun Maan etäisyyttä Auringosta merkitään AU, niin MU on noin 0,4 AU. Voidaan laskea etäisyyksiä eri planeetoille yksikössä MU ja etsiä lainalaisuuksia näiden välille.

Planeetta	AU	MU	MU Merkuriuksesta	Etäisyyssuhde edeltävään planeettaan
Merkurius	0,387	1	0	-
Venus	0,723	1,868	0,868	-
Maa	1,0	2,584	1,584	1,825
Mars	1,524	3,938	2,938	1,855
(asteroidit)	2,77	7,158	6,158	2,096
Jupiter	5,203	13,444	12,444	2,021
Saturnus	9,539	24,649	23,649	1,9
Uranus	19,18	49,561	48,561	2,053
Neptunus	30,06	77,674	76,674	1,579
(plutinot)	39,5	102,067	101,067	2,081 Uranuksesta

Karke Cohenin sääntö ottaa lukuun Neptunuksen:

1/2, 3/4, 1, 1½, 2½, 5, 10, 20, 30 ja 40 AU.

Muita lainalaisuuksia

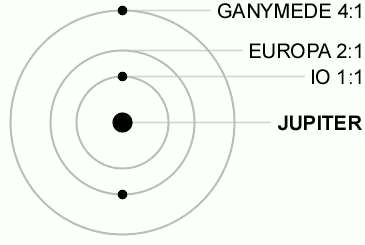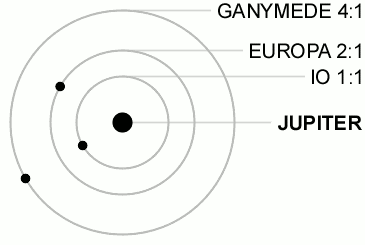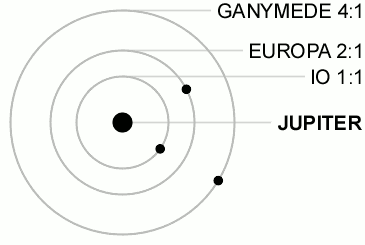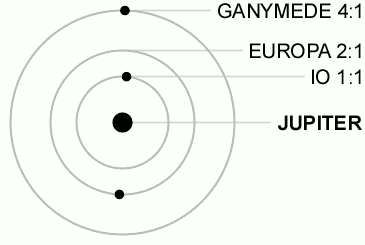
Laplacen resonanssi Jupiterin kuissa

Aurinkokunnassa on esimerkiksi kuiden ratojen välillä säännönmukaisuuksia. Neljä Jupiterin suurinta kuuta ovat resonanssissa keskenään, kiertoaikojen suhde on vakio. Sisempi suuri kuu Amalthea on mukana samassa sarjassa, jossa kiertoaikojen suhde on 1:2:4:8. Uloin suuri kuu Kallisto aiheuttaa vuorovesilukituksen, joka ohjaa muita kuita. Jupiterin kuille d = 2n-1 + 0.5, jossa n = 0, 1, 2, 3. Amalthealle n =−∞.

Uranuksen suurilla kuilla on säännöllinen, muttei Boden lakia seuraava etäisyysjakauma jossa d = (n + 1)/2 jossa n = 1, 2, 3, 6,8.

Kolmen planeetan kuujärjestelmiä kuvaa Dermottin laki

$T(n)=T(0)C^{n}$

jossa

n = 1,2,3 ..

T(n) on n:nen kuun sideerinen kiertoaika.

T(0) on luokkaa 0,46 ja C on vakio.

Jupiterin kuut: T(0) = 0,444; C = 2,03
Saturnuksen kuut: T(0) = 0,462; C = 1,59
Uranuksen kuut: T(0) = 0,488; C = 2,24

Monille eksoplaneetoille on löydetty peräkkäisten planeettojen kiertoaikojen suhteita 1:2 eli 1:2 resonansseja. Rataresonanssien pysyvyys riippuu kiertoaikojen suhteiden lisäksi siitä, ovatko planeetat ollessaan radan samassa pisteessä toistensa kanssa samassa vai esimerkiksi vastakkaisessa suunnassa aurinkoon nähden. Häiriöiden ansiosta planeettojen rataellipsit kiertyvät ja muut rata-arvot muuttuvat aikojen kuluessa.

Lähteet

Aiheesta muualla

The Titius-Bode Number Sequence Deciphered (Arkistoitu – Internet Archive)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] ttp://iopscience.iop.org/1538-3881/124/6/3430/202320.text.html

[Nimetön-rG7T-1-2] ttps://web.archive.org/web/20060204183337/http://www.planetary.org/explore/topics/trans_neptunian_objects/facts.html

[3] ttps://web.archive.org/web/20060831005444/http://www.planetary.org/explore/topics/our_solar_system/asteroids_and_comets/ceres.html

[4] ttp://hubblesite.org/newscenter/archive/releases/2007/27/background/

[5] ttp://aa.usno.navy.mil/faq/docs/minorplanets.php (Arkistoitu – Internet Archive)

[6] ttp://www.iau.org/public/pluto/