Stern–Volmer-kuvaaja

Molekyylin absorboidessa säteilyä sen perustilan( ${\displaystyle S_{0}}$ ) elektroni virittyy energeettisesti ylempään energiatilaan, joka on tyypillisesti ensimmäinen viritystila ( ${\displaystyle S_{1}}$ ). Molemmat ovat singlettitiloja.^A Viritystila lopulta sammuu molekyylitörmäyksen seurauksena yhtälön (1) mukaisesti:

(1)${\displaystyle \qquad {\text{S}}_{1}+{\text{Q}}{\overset {\textstyle k_{q}}{\underset {}{\longrightarrow }}}\;{\text{S}}_{0}+{\text{Q}}}$

Tässä ${\displaystyle Q}$ on törmäyskappale ja -molekyyli, ${\displaystyle k_{q}}$ on viritystilan sammumisen nopeusvakio ja se sisältää erityyppiset fotofysikaaliset molekyylin eri energiatilojen välillä tapahtuvat elektronisiirtymät. Yhtälön (1) nopeuslaiksi voidaan kirjoittaa:

(2)${\displaystyle \qquad R\,=\,k_{\text{q}}[{\text{S}}_{1}][{\text{Q}}]}$

Viritystilan elinaika on lyhyt, joten siihen voidaan soveltaa vakiotilaoletusta:

(3)${\displaystyle \qquad {\frac {d[{\text{S}}_{1}]}{dt}}\,=\,k_{\text{abs}}[{\text{S}}_{0}]-k_{_{\text{F}}}[{\text{S}}_{1}]-k_{_{\text{IC}}}[{\text{S}}_{1}]-k_{_{\text{ISC}}}^{\text{s}}[{\text{S}}_{1}]-k_{\text{q}}[{\text{S}}_{1}][{\text{Q}}]=0}$

Tässä ${\displaystyle k_{\text{abs}}}$ on absorption, ${\displaystyle k_{_{\text{F}}}}$ on virittyneen singlettitilan sammumisen, ${\displaystyle k_{\text{IC}}}$ on singlettitilalta perustilalle tapahtuvan siirtymisen, ja ${\displaystyle k_{_{\text{ISC}}}^{\text{s}}}$ singlettitilalta triplettitilalle tapahtuvan siirtymisen nopeusvakio.

Määritelmän mukaan singlettitilan sammumiseen liittyvä fluoresenssin keskimääräinen elinaika on

(4)${\displaystyle \qquad {\frac {1}{\tau _{_{\text{F}}}}}\,=\,k_{_{\text{F}}}+k_{_{\text{IC}}}+k_{_{\text{ISC}}}^{\text{s}}+k_{\text{q}}[{\text{Q}}]}$

Sijoittamalla yhtälö (4) yhtälöön (3) voidaan viritystilan konsentraatioksi saada: ${\displaystyle [{\text{S}}_{1}]=k_{\text{abs}}[{\text{S}}_{0}]\tau _{_{\text{F}}}}$. Kun lisäksi fluoresenssin voimakkuus, ${\displaystyle I_{_{\text{F}}}}$, riippuu fluoresenssin nopeudesta: ${\displaystyle I_{\text{F}}=k_{_{\text{F}}}[{\text{S}}_{1}]=k_{\text{abs}}[{\text{S}}_{0}]k_{_{\text{F}}}\,\tau _{_{\text{F}}}}$, saadaan fluoresenssin kvanttisuhteelle, ${\displaystyle \Phi _{_{\text{F}}}}$, (engl. quantum yield) yhtälö (5).

(5)${\displaystyle \qquad k_{_{\text{F}}}\,\tau _{_{\text{F}}}\,=\,{\frac {k_{_{\text{F}}}}{{k_{_{\text{F}}}}+k_{_{\text{IC}}}+k_{_{\text{ISC}}}^{\text{s}}+k_{\text{q}}[{\text{Q}}]}}\,=\,\Phi _{_{\text{F}}}}$

Yhtälössä oleva osamäärä tarkoittaa fluoresenssin nopeusvakio jaettuna kaikkien nopeusvakioiden summalla, jotka johtavat viritystilan sammumiseen. Tätä vastaava tapahtuma on todettavissa rinnakkaisissa alkeisreaktioissa. Fluoresenssin kvanttisuhde on määritelty myös olemaan: fluoresenssina emittoituneiden fotonien lukumäärä jaettuna absorboituneiden fotonien lukumäärällä. Kun yhtälöön (5) sijoitetaan em. ${\displaystyle I_{\text{F}}}$ ja otetaan yhtälöstä puolittain kännteisarvot, saadaan:[1]

(6)${\displaystyle \qquad {\frac {1}{I_{_{\text{F}}}}}\,=\,{\frac {1}{k_{\text{abs}}[{\text{S}}_{0}]}}{\Bigg (}1+{\frac {k_{_{\text{IC}}}+k_{_{\text{ISC}}}^{\text{s}}}{k_{_{\text{F}}}}}{\Bigg )}+{\frac {k_{\text{q}}[{\text{Q}}]}{k_{\text{abs}}[{\text{S}}_{0}]k_{_{\text{F}}}}}}$

Fluoresenssimittauksen analyysi

Mittauspistejoukkoon on sovitettu suoran yhtälö. Pistejoukon suorankaltaisuus kuvastaa tässä yhtälön (7) tarkkuutta. Pistejoukon lineaarisuudesta poikkeava sijoittuminen viittaisi siihen, että jokin muu säteilyksetön energian siirtotapahtuma olisi myös läsnä.

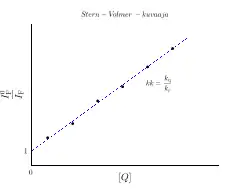
Määritettäessä fluoresenssin sammumista, mitataan fluoresenssin voimakkuus sammuttajan konsentraation funktiona, ${\displaystyle [Q]}$. Lopuksi mittauksia suhteutetaan tilanteeseen, jossa sammuttajaa ei ole läsnä,${\displaystyle I_{_{\text{F}}}^{0}}$ yhtälön (7), jota sanotaan Stern-Volmer -yhtälöksi, mukaisesti.

(7)${\displaystyle \qquad {\frac {I_{_{\text{F}}}^{0}}{I_{_{\text{F}}}}}\,=\,1+{\frac {k_{\text{q}}}{k_{_{\text{F}}}}}[Q]}$

Piirrettäessä fluoresenssien voimakkuuksien suhde sammuttajan konsentraation funktiona, on seurauksena kuvaajalla suora, jonka kulmakerroin on ${\displaystyle {\frac {k_{\text{q}}}{k_{_{\text{F}}}}}}$. Tätä kutsutaan Stern-Volmer-kuvaajaksi. Siinä sovitettu suora on pakotettu leikkaamaan y-akseli pisteessä y=1.[1]

^A Kyseessä on elektroninen viritystila. Sinlettitilan kahdella elektronilla on vastakkaiset spinnit. Triplettitilassa ne ovat samansuuntaiset.