Pistetulo

Kahden vektorin A = [A₁, A₂, ..., A_n] ja B = [B₁, B₂, ..., B_n] pistetulo n-ulotteisessa avaruudessa määritellään seuraavasti:[2]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =\sum _{i=1}^{n}A_{i}B_{i}=A_{1}B_{1}+A_{2}B_{2}+\cdots +A_{n}B_{n}}$

missä ${\displaystyle \sum }$ tarkoittaa summausta. Esimerkiksi kolmi­ulotteisessa avaruudessa vektorien [1, 3, -5] ja [4, -2, -1] pistetulo on:

${\displaystyle {\begin{aligned}\ [1,3,-5]\cdot [4,-2,-1]&=1\cdot 4+3\cdot (-2)+(-5)\cdot (-1)\\&=4-6+5\\&=3.\end{aligned}}}$

Euklidisessa avaruudessa vektori on geometrinen olio, jolla on sekä suuruus että suunta. Vektoria voidaan kuvata nuolella. Sen suuruus on nuolen pituus ja suunta se, mihin nuolen kärki osoittaa. Vektorin A pituudelle käytetään merkintää ${\displaystyle \left\|\mathbf {A} \right\|}$. Euklidisten vektorien A ja B piste­tulo määritellään seuraavasti: [3][4]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =\left\|\mathbf {A} \right\|\,\left\|\mathbf {B} \right\|\cos \theta ,}$

missä ${\displaystyle \theta }$ on vektorien A ja B välinen kulma.

Erityisesti jos A ja B ovat kohtisuorassa, niiden välinen kulma on 90° ja

${\displaystyle \mathbf {A} \cdot \mathbf {B} =0.}$

Toinen ääritapaus on, että vektorit ovat samansuuntaisia. Silloin niiden välinen kulma on 0° ja

${\displaystyle \mathbf {A} \cdot \mathbf {B} =\left\|\mathbf {A} \right\|\,\left\|\mathbf {B} \right\|}$

Tästä seuraa, että vektorin A pistetulo itsensä kanssa on

${\displaystyle \mathbf {A} \cdot \mathbf {A} =\left\|\mathbf {A} \right\|^{2},}$

mistä saadaan vektorin pituudelle lauseke

${\displaystyle \left\|\mathbf {A} \right\|={\sqrt {\mathbf {A} \cdot \mathbf {A} }}.}$

Skalaariprojektio

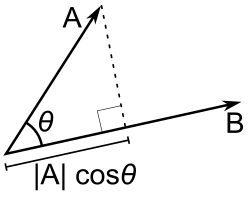
Euklidisen vektorin A skalaariprojektio eli skalaarinen komponentti toisen euklidisen vektorin B suunnassa on määritelmän mukaan

${\displaystyle A_{B}=\left\|\mathbf {A} \right\|\cos \theta ,}$

missä ${\displaystyle \theta }$ on vektorien A ja B välinen kulma.

Pistetulon geometriseen määritelmään perustuen tämä voidaan kirjoittaa myös muotoon

${\displaystyle A_{B}=\mathbf {A} \cdot {\widehat {\mathbf {B} }},}$

missä ${\displaystyle {\widehat {\mathbf {B} }}=\mathbf {B} /\left\|\mathbf {B} \right\|}$ on B:n suuntainen yksikkövektori.

Pistetulon vaihdantalaki

Pistetuloa luonnehtii näin ollen geometrisesti[5]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =A_{B}\left\|\mathbf {B} \right\|=B_{A}\left\|\mathbf {A} \right\|.}$

Tähän tapaan määriteltynä pistetulo on homogeeninen skaalattaessa jokaista muuttujaa, mikä merkitsee, että jokaiselle skalaarille ${\displaystyle \alpha }$ pätee:

${\displaystyle (\alpha \mathbf {A} )\cdot \mathbf {B} =\alpha (\mathbf {A} \cdot \mathbf {B} )=\mathbf {A} \cdot (\alpha \mathbf {B} ).}$

Pistetulolle pätee myös osittelulaki, toisin sanoen

${\displaystyle \mathbf {A} \cdot (\mathbf {B} +\mathbf {C} )=\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \cdot \mathbf {C} .}$

Näistä ominaisuuksista yhteen­vetona voidaan todeta, että pistetulo on bilineaarinen muoto. Lisäksi tämä bilineaarinen muoto on positiivinen definiittinen,[1] mikä merkitsee, että ${\displaystyle \mathbf {A} \cdot \mathbf {A} }$ ei ole koskaan negatiivinen, ja nolla se on jos ja vain jos ${\displaystyle \mathbf {A} =\mathbf {0} .}$

Jos e₁, ..., e_n ovat ${\displaystyle \mathbb {r} ^{n}}$:n standardikanta eli koordinaattiakselien suuntaiset yksikkövektorit, voidaan kirjoittaa:

${\displaystyle {\begin{aligned}\mathbf {A} &=[A_{1},\dots ,A_{n}]=\sum _{i}A_{i}\mathbf {e} _{i}\\\mathbf {B} &=[B_{1},\dots ,B_{n}]=\sum _{i}B_{i}\mathbf {e} _{i}.\end{aligned}}}$

Vektorit e_i muodostavat avaruuden ortonormaalin kannan, sillä ne kaikki ovat yhden pituusyksikön pituisia ja keskenään kohtisuorassa. Koska ne ovat yksikön pituisia, on

${\displaystyle \mathbf {e} _{i}\cdot \mathbf {e} _{i}=1}$

ja koska ne ovat keskenään kohtisuorassa, jos ${\displaystyle i\neq j}$, on

${\displaystyle \mathbf {e} _{i}\cdot \mathbf {e} _{j}=0.}$

Tällöin voidaan todeta, että kaikissa tapauksissa pätee:

${\displaystyle \mathbf {e} _{i}\cdot \mathbf {e} _{j}=\delta _{ij}.}$

missä ${\displaystyle \delta _{i}j}$ on Kroneckerin delta.

Geometrisen määritelmän perusteella voidaan toisaalta todeta, että jokaiselle kanta­vektorille e_i ja jokaiselle vektorille A pätee:

${\displaystyle \mathbf {A} \cdot \mathbf {e} _{i}=\left\|\mathbf {A} \right\|\,\left\|\mathbf {e} _{i}\right\|\cos \theta =\left\|\mathbf {A} \right\|\cos \theta =A_{i},}$

missä A_i on vektorin A komponentti yksikkö­vektorin e_i suunnassa.

Soveltamalla geometrisesti määritellyn pistetulon osittelulakia saadaan

${\displaystyle \mathbf {A} \cdot \mathbf {B} =\mathbf {A} \cdot \sum _{i}B_{i}\mathbf {e} _{i}=\sum _{i}B_{i}(\mathbf {A} \cdot \mathbf {e} _{i})=\sum _{i}B_{i}A_{i},}$

mikä on täsmälleen sama kuin pistetulon algebrallinen määritelmä. Kahden vektorin geometrinen pistetulo on siis aina yhtä suuri kuin niiden algebrallinen pistetulo.

Kolmio, jonka kahtena sivuna ovat vektorit a ja b, joiden välinen kulma on ${\displaystyle \theta }$.

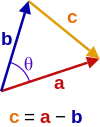
Oletetaan kaksi vektoria, a ja b, joiden välinen kulma ${\displaystyle \theta }$, kuten oheisessa kuvassa. Niiden avulla voidaan muodostaa kolmio, jonka kolmantena sivuna on vektori c = a - b. Tämän kolmannen sivun pistetulo itsensä kanssa on:

${\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )}$

${\displaystyle =\mathbf {a} \cdot \mathbf {a} -\mathbf {a} \cdot \mathbf {b} -\mathbf {b} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} }$

${\displaystyle =a^{2}-\mathbf {a} \cdot \mathbf {b} -\mathbf {a} \cdot \mathbf {b} +b^{2}}$

${\displaystyle =a^{2}-2\mathbf {a} \cdot \mathbf {b} +b^{2}}$

Näin ollen on:

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \theta }$,

mikä tulos tunnetaan kosinilauseena.[9]

Sovellettuina vektoreihin, joiden komponentit ovat kompleksilukuja, edellä esitetyt pistetulon määritelmät antaisivat sille varsin erilaisia ominaisuuksia. Esimerkiksi vektorin pistetulo itsensä kanssa voisi olla mikä tahansa kompleksi­luku, ja se voisi myös olla nolla, vaikka kyseessä ei olisikaan nollavektori; sellaisia vektoreita sanotaan isotrooppisiksi; tällä taas olisi pituuden ja kulman käsitteisiin liittyviä seurauksia. On kuitenkin mahdollista määritellä kompleksi­vektoreillekin pistetulo siten, että se on ominaisuuksiltaan lähempänä reaali­vektoreiden pistetuloa ja että sillä esimerkiksi on aina positiivis-definiittinen normi. Tällöin pistetulo määritellään seuraavasti:[2]

${\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}},}$

missä b_i on b_i:n kompleksikonjugaatti.

Näin määriteltynä jokaisen vektorin pistetulo itsensä kanssa on ei-negatiivinen reaaliluku, ja se on nolla vain, jos kyseessä on nollavektori. Näin määritellyllä kompleksi­vektorien piste­tulolla ei kuitenkaan ole reaali­vektorien pistetulon symmetria­ominaisuuksia eikä se ole bilineaarinen. Sen sijaan se on seskvilineaarinen: se on konjugaattilineaarinen, mutta ei lineaarinen b:n suhteen. Se ei myöskään symmetrinen, sillä

${\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}.}$[1]

Kompleksivektorien välinen kulma määritellään tällöin seuraavasti:

${\displaystyle \cos \theta ={\frac {\operatorname {Re} (\mathbf {a} \cdot \mathbf {b} )}{\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|}}.}$

Tämäntyyppinen skalaaritulo on kaikesta huolimatta käyttö­kelpoinen, ja se johtaa hermiittisen muodon ja yleisen sisätulo­avaruuden käsitteisiin.

Sisätulo on pistetulon yleistys abstarkteihin vektori­avaruuksiin, joiden kerroin­kuntana on joko reaalilukujen (${\displaystyle \mathbb {R} }$) tai kompleksilukujen kunta (${\displaystyle \mathbb {C} }$). Sisätulolle käytetään yleensä merkintää ${\displaystyle \left\langle \mathbf {a} \,,\mathbf {b} \right\rangle }$.

Kun kerroinkuntana ovat kompleksiluvut, kahden vektorin sisätulo on yleensä kompleksiluku, ja sisätulo on seskvilineaarinen, ei bilineaarinen. Sisätuloavaruus on normitettu vektoriavaruus, ja vektorin sisätulo itsensä kanssa on positiivis-definiittinen.

Sisätulo on määritelty vektoreille, joilla on äärellinen määrä komponentteja. Koska vektorit voidaan esittää lukujonoina^selvennä, voidaan n-vektori käsittää myös diskreetiksi funktioksi, joka on määritelty joukossa ${\displaystyle {k\in N|1<=k<=n}}$, jolloin u_i eli vektorin i:s komponentti on funktion arvo argumentin arvolla i.

Tämä käsite voidaan yleistää jatkuville funktiolle. Samoin kuin vektorien sisätulo lasketaan vastaavien komponenttien tulojen summana, funktion sisätulo määritellään integraalina jonkin välin a < x b yli, jolle välille käytetään myös merkintää [a,b]:[2]

${\displaystyle \left\langle u,v\right\rangle =\int _{a}^{b}u(x)v(x)dx}$

Tämä voidaan edelleen yleistää kompleksifunktioille ${\displaystyle \psi (x)}$ ja ${\displaystyle \chi (x)}$ samaan tapaan kuin kompleksivektorien sisätulo edellä määriteltiin. Tällöin saadaan:[2]

${\displaystyle \left\langle \psi ,\chi \right\rangle =\int _{a}^{b}\psi (x){\overline {\chi (x)}}dx.}$

Sisätuloilla voi olla painofunktio, toisin sanoen funktio, joka painottaa sisätulon jokaista termiä jollakin arvolla.

Matriiseilla sisätuloa vastaa Frobeniuksen sisätulo, joka on analoginen vektorien sisätulon kanssa. Kahden matriisin Frobeniuksen sisätulo on määritelty edellyttäen, että kummassakin on yhtä monta riviä ja yhtä monta saraketta. Tällöin matriisien A ja B sisätulo on niiden vastaavien komponenttien tulojen summa:

${\displaystyle \mathbf {A}$ :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}{\overline {B_{ij}}}=\mathrm {tr} (\mathbf {B} ^{\mathrm {H} }\mathbf {A} )=\mathrm {tr} (\mathbf {A} \mathbf {B} ^{\mathrm {H} }).}

${\displaystyle \mathbf {A}$ :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}B_{ij}=\mathrm {tr} (\mathbf {B} ^{\mathrm {T} }\mathbf {A} )=\mathrm {tr} (\mathbf {A} \mathbf {B} ^{\mathrm {T} })=\mathrm {tr} (\mathbf {A} ^{\mathrm {T} }\mathbf {B} )=\mathrm {tr} (\mathbf {B} \mathbf {A} ^{\mathrm {T} }).} (reaalikertoimisille matriiseille)

Samaan tapaan myös dyadeille on määritelty sisätulo ja "kaksinkertainen" sisätulo.

Kahden tensorin sisätulo, joista toinen on astetta n ja toinen astetta m, on asteen n + m − 2 tensori.