Sirkulaatio

Vektorikentän viivaintegraali suljetun käyrän yli on sen kierto[1] eli sirkulaatio (engl. circulation) tuon käyrän ympäri. Sirkulaatiota merkitään Γ:lla (iso kreikkalainen gamma-kirjain). Jos ${\textstyle \mathbf {F} }$ on jatkuva vektorikenttä ja ${\textstyle {\mathcal {C}}}$ on suljettu käyrä, jonka parametrisaatio on ${\textstyle \mathbf {r}$ , niin ${\textstyle \mathbf {F} }$ :n sirkulaatio ${\textstyle {\mathcal {C}}}$ :n ympäri on integraali

\Gamma =\oint _{\mathcal {C}}\mathbf {F} \cdot \mathrm {d} \mathbf {r}

[2][3]

Vektorikentän

{\textstyle \mathbf {F} }

sirkulaatio suljetun käyrän

{\textstyle {\mathcal {C}}}

ympäri on

\Gamma =\oint _{\mathcal {C}}\mathbf {F} \cdot \mathrm {d} \mathbf {r} =\oint _{\mathcal {C}}\Vert \mathbf {F} \Vert \cos \theta \,\mathrm {d} r

.

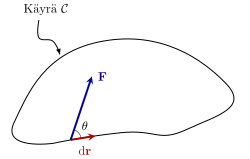
Integraalimerkissä oleva rengas painottaa sitä, että käyrä ${\textstyle {\mathcal {C}}}$ on suljettu.

Stokesin lauseen mukaan vektorikentän kierto käyrän C ympäri vastaa vektorikentän roottorin integraalia minkä tahansa käyrän rajaaman pinnan S yli:

\oint _{\mathcal {C}}\mathbf {F} \cdot \mathrm {d} \mathbf {s} =\int _{\mathcal {S}}\nabla \times \mathbf {F} \cdot \mathrm {d} \mathbf {a}

,

missä da on pinta-ala-alkio, joka on pintaa vastaan kohtisuora, ja jonka etumerkki määräytyy oikean käden säännön mukaisesti käyrän kiertosuunnan perusteella.

Sirkulaatio virtausmekaniikassa

Virtausmekaniikassa vektorikenttä ${\textstyle \mathbf {F} =\mathbf {v} (x,y,z)=v_{x}(x,y,z)\,\mathbf {i} +v_{y}(x,y,z)\,\mathbf {j} +v_{z}(x,y,z)\,\mathbf {k} }$ on nesteen tai kaasun nopeus. Tällöin nopeuskentän sirkulaatio suljetun käyrän ympäri kertoo käyrän sisäpuolelle jäävien pyörteiden voimakkuudesta. Vapaan vorteksin, jonka voimakkuus on ${\textstyle K}$ , tapauksessa nopeuskentän sirkulaatio vorteksin ympäri on

$\Gamma =2\pi K$ .[3]

Stokesin lausetta käyttämällä nähdään, että pyörteettömän virtauksen ( $\nabla \times \mathbf {v} =0$ ) sirkulaatio minkä tahansa suljetun käyrän ympäri on nolla: Merkitään käyrän ${\textstyle {\mathcal {C}}}$ rajaamaa pintaa ${\textstyle {\mathcal {S}}}$ :llä, jolloin Stokesin lauseen mukaan

$\Gamma =\oint _{\mathcal {C}}\mathbf {v} \cdot \mathrm {d} \mathbf {r} =\iint _{\mathcal {S}}\left(\nabla \times \mathbf {v} \right)\cdot \mathrm {d} \mathbf {S} =0$ .

Kutta–Žukovski-teoreema

Lentokoneen siipeen kohdistuva nostovoima lasketaan Kutta–Žukovski-teoreeman mukaan käyttäen ilmavirran nopeuden sirkulaatiota siipiprofiilin reunakäyrän ympäri.

Pääartikkeli: Kutta–Žukovski-teoreema

Virtaukseen asetettuun lieriöön kohdistuvan nostovoiman suuruus ${\textstyle L}$ riippuu virtauksen nopeuskentän sirkulaatiosta lieriön poikkipinnan reunakäyrän ympäri:

${\frac {L}{b}}=-\rho U_{\infty }\Gamma$ ,[4]

missä

{\textstyle b}

on lieriön pituus (virtauksen sisällä oleva osa),

{\textstyle \rho }

on ympäröivän fluidin tiheys ja

{\textstyle U_{\infty }}

on vapaan virtauksen vauhti kaukana lieriöstä.

Miinusmerkki yhtälössä johtuu siitä, että nostovoiman suunta on 90° virtauksen suunnasta sirkulaation kiertosuuntaa vastaan.[4]

Lähteet

Väisälä, Kalle: Vektorianalyysi, s. 62. WSOY, 1968.
Adams, Robert A. & Essex, Christopher: Calculus, A Complete Course, s. 880. 8. painos. Toronto: Pearson, 2014. ISBN 978-0-32-178107-9. (englanniksi)
White, Frank M.: Fluid Mechanics, s. 550−555. 7th Edition in SI Units. Singapore: McGraw-Hill, 2011. ISBN 978-007-131121-2. (englanniksi)
White, s. 561

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Väisälä, Kalle: Vektorianalyysi, s. 62. WSOY, 1968.

[2] Adams, Robert A. & Essex, Christopher: Calculus, A Complete Course, s. 880. 8. painos. Toronto: Pearson, 2014. ISBN 978-0-32-178107-9. (englanniksi)

[:0-3] White, Frank M.: Fluid Mechanics, s. 550−555. 7th Edition in SI Units. Singapore: McGraw-Hill, 2011. ISBN 978-007-131121-2. (englanniksi)

[:1-4] White, s. 561