Schläflin symboli

Säännölliset kuperat ja tähtimäiset monikulmiot kolmioista 12-kulmioihin ja niiden Schäflin symbolit

Kuperan säännöllisen p-kulmion Schläflin symboli on {p}. Esimerkiksi säännöllinen viisikulmio merkitään {5}.

Ei-kuperille tähtimonikulmioille käytetään konstruktiivista merkintä p/s, missä p on kärkien lukumäärä ja s-1 on niiden kärkien lukumäärä, jotka sivuutetaan piirrettäessä mikä tahansa tähtimonikulmion sivu. Esimerkiksi {5/2} esittää pentagrammia.

Säännöllisen monitahokkaan Schläflin symboli on {p,q}, jos sen sivut ovat p-kulmioita ja jokaista kärkeä ympäröi q tahkoa, jolloin monitahokkaan kärkikuvio on q-kulmio.

Viiden kuperan Platonin kappaleen Schläfflin symbolit ovat:[2]

nimi	kuva	Schläflin symboli
tetraedri		{3,3}
kuutio		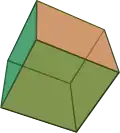{4,3}
oktaedri		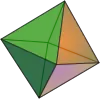{3,4}
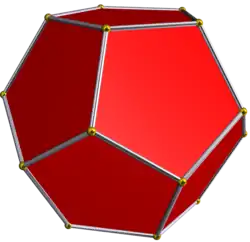
dodekaedri		{5,3}
ikosaedri		{3,5}

Esimerkiksi dodekaedrin Schläflin symboli on {5,3}, koska sen sivutahkot ovat säännöllisiä viisikulmioita ja jokaisessa kärjessä toisensa kohtaa kolme sivutahkoa.

Lisäksi on olemassa neljä ei-kuperaa säännöllistä Keplerin–Poinsot’n kappaletta. Niiden Schläfflin symbolit ovat:[2]

nimi	kuva	Schläflin symboli
pieni tähtidodeaedri:		{5/2, 5}
suuri tähtidodekaedri		{5/2, 3}
suuri dodekaedri		{5, 5/2}
suuri ikosaedri		{3, 5/2}.

Topologisesti säännölliset kaksiulotteiset tessellaatiot voidaan rinnastaa monitahokkaisiin, joissa kuitenkin samaan särmään ulottuvien tahkojen kulmien summa on 360 astetta. Niinpä niille voidaan määritellä Schälflin symbolit samalla tavalla kuin monitahokkaillekin. Ainoat säännölliset monikulmiot, joilla euklidinen taso voidaan täyttää, ovat tasasivuiset kolmiot, neliöt ja säännölliset kuusikulmiot. Vastaavat tessellaatiot ja niiden Schläflin symbolit ovat seuraavat:[3]

nimi	kuva	Schläflin symboli
kolmiolaatoitus		{3, 6}
neliölaatoitus, ruudukko		{4, 4}
kuusikulmiolaatoitus		{6, 3}

Myös korkeammissa ulottuvuuksissa pätee vastaava analogia monitahokkaita vastaavien polytooppien ja tessellaatioiden välillä.

Säännöllisen 4-polytoopin Schläflin symboli on muotoa {p,q,r}. Sen kaksiulotteiset sivutahkot ovat säännöllisiä p-kulmioita ({p}), solut säännöllisiä monitahokkaita tyyppiä {p,q}, kärkikuviot säännöllisiä monitahokkaita tyyppiä {q,r} ja särmäkuviot säännöllisiä r-kulmioita (tyyppiä {r}).

On olemassa neljä säännöllistä kuperaa 4-polytooppia sekä 10 ei-kuperaa säännöllistä tähtimäistä 4-polytooppia. Esimerkiksi 120-soluisen polytoopin Scläflin symboli on {5,3,3}. Sen solut ovat dodekaedreja ({5,3}), ja kunkin särmän ympärillä on kolme solua.[4]

Kolmiulotteisella euklidisella avaruudella on vain yksi säännöllinen tessellaatio, avaruuden jakaminen kuutioiksi.[5] Tämän tessellaation Schläflin symboli on {4,3,4}, ja siinä jokainen särmä on yhteinen neljälle kuutiolle.

On myös neljä säännöllistä kompaktia hyperbolista tessellaatiota. Esimerkiksi Schläflin symboli {5,3,4} tarkoittaa pientä hyperbolista dodekaedristä hunajakennoa, joka täyttää avaruuden dodekaedrin muotoisilla soluilla.

Korkeampiulotteisten säännöllisten polytooppien Schläflin symbolit määritellään rekursiivisesti. Ne ovat muotoa {p₁, p₂, ..., p_n - 1}, kun n-polytoopin n-1 -ulotteisen sivun Schäflin symboli on {p₁,p₂, ..., p_n - 2} ja särmäkuvion {p₂,p₃, ..., p_n - 1}.

Polytoopin sivun särmäkuvio ja saman polytoopin särmäkuvion sivu ovat samat:{p₂,p₃, ..., p_n - 2}.

Viidessä tai useammassa ulottuvuudessa on vain kolme säännöllistä polytooppia: simpleksi {3,3,3,...,3}, ristipolytooppi {3,3, ..., 3,4}; and the hyperkuutio, {4,3,3,...,3}. Ne voidaan käsittää tetraedrin, oktaedrin ja kuution korkeampiulotteisiksi vastineiksi.[6] Ei-kuperia säännöllisiä polytooppeja ei useammassa kuin neljässä ulottuvuudessa ole.

Jos vähintään kaksiulotteisen polytoopin Scläflin symboli on {p₁,p₂, ..., p_n - 1}, sen duaalipolytoopin Schläflin symbolissa ovat samat luvut takaperoisessa järjestyksessä: {p_n - 1, ..., p₂,p₁}.

Jos lukujono on palindrominen eli sama etuperin ja takaperin, polytooppi on itseduaalinen. Jokainen säännöllinen kaksiulotteinen polytooppi eli monikulmio on itseduaalinen.

Uniformiset prismaattiset polytoopit voidaan määritellä ja nimetä alempiulotteisten säännöllisten polytooppien karteesisina tuloina, operaattorina "×". Niinpä:

• Nollassa ulottuvuudessa piste merkitään ( ). Sen Coexterin diagrammi on tyhjä, Coexterin merkintää käyttämällä sen symmetria on ][.
• Yhdessä ulottuvuudessa jana merkitään { }. Sen Coexterin diagrammi on . Sen symmetria on [ ].
• Kahdessa ulottuvuudessa suorakulmio merkitään { } × { }. Sen Coexterin diagrammi on
• Kolmessa ulottuvuudessa p-kulmainen prisma merkitään { } × {p}. Sen Coexterin diagrammi on . Sen symmetria on [2,p].
• Neljässä ulottuvuudessa uniforminen {p,q}-tahoinen prisma merkitään { } × {p,q}. Sen Coexterin diagrammi on . ja symmetria [2,p,q].
• Neljässä ulottuvuudessa uniforminen p-q-duoprisma merkitään {p} × {q}. Sen Coexterin diagrammi on ja symmetria [p,2,q].

Prismojen duaalikappaleet eli bipyramidit voidaan myös esittää yhdistetyillä symboleilla, joissa kuitenkin edellisestä poiketen käytetään yhteenlaskuoperaattoria +. Niinpä:

• Kahdessa ulottuvuudessa neljäkäs (rombi) merkitään { } + { }. Sen Coexterin diagrammi on ja symmetria [2].
• Kolmessa ulottuvuudessa p-kulmainen bipyramidi merkitään { } + {p}. Sen Coexterin diagrammi on ja symmetria [2,p].
• Neljässä ulottuvuudessa {p,q}-tahoinen bipyramidi merkitään { } + {p,q}. Sen Coexterin diagrammin on ja symmetria [p,q].
• Neljässä ulottuvuudessa p-q -duopyramidi merkitään {p} + {q}. Sen Coexterin diagrammi on ja symmetria [p,2,q].

Pyramidimaiset polytoopit, joissa yksi tai useampi kärki suuntautuu kohtisuorasti ulospäin muiden muodostamasta kuviosta, voidaan esittää yhdistämistä tarkoittavan operaattorin "∨" avulla. Tällaiset polytoopit voidaan katsoa kahden polytoopin yhdistelmiksi, joista toisen jokainen kärki yhdistetään särmällä toisen jokaiseen kärkeen. Niinpä:

• Kahdessa ulottuvuudessa tasakylkinen kolmio merkitään ( ) ∨ { } = ( ) ∨ [( ) ∨ ( )].
• Kolmessa ulottuvuudessa :
  • digonaalinen disfenoidi merkitään { } ∨ { } = [( ) ∨ ( )] ∨ [( ) ∨ ( )].
  • pyramidi, jonka pohja on säännöllinen p-kulmio, merkitään ( ) ∨ {p}.
• Neljässä ulottuvuudessa:
  • p-q-tahoinen pyramidi merkitään ( ) ∨ {p,q}.
  • 5-solu merkitään ( ) ∨ [( ) ∨ {3}] tai [( ) ∨ ( )] ∨ {3} = { } ∨ {3}.
  • Neliöpyramidaalinen pyramidi merkitään ( ) ∨ [( ) ∨ {4}] tai [( ) ∨ ( )] ∨ {4} = { } ∨ {4}.

Operaatioita yhdistettäessä laskujärjestys ylimmästä alimpaan on ×, +, ∨.

Aksiaaliset polytoopit, joissa kärjet ovat yhdensuuntaisilla hypertasoilla, voidaan merkitä operaattorilla ||. Uniforminen prisma on {n}||{n} ja antiprisma {n}||r{n}.

Katkaistussa monikulmiossa on kaksi kertaa niin monta sivua kuin alkuperäisessä. Säännöllinen monikulmio, jossa sivujen lukumäärä on parillinen, se voidaan puolittaa. Jos säännöllisessä n-kulmiossa, jossa n on parillinen, jokainen kärki yhdistetään siihen nähden kahden sivun takana olevaan kärkeen, saadaan kahdesta n/2-kulmiosta muodostuva tähtikuvio 2{n}.

Muoto	Schläflin symboli	Symmetria	Coxeterin diagrammi		Esimerkki, {6}
Säännöllinen	{p}	[p]		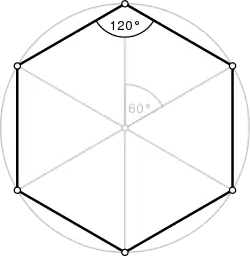		Kuusikulmio
Katkaistu	t{p} = {2p}	[[p]] = [2p]	=			Katkaistu kuusikulmio (12-kulmio)	=
Tähtikuvio	a{2p} = ß{p}	[2p]	=			Heksagrammi	=
Puolitettu	h{2p} = s{p} = {p}	[1+,2p] = [p]	= =			Puolitettu kuusikulmio (kolmio)	= =

Coxeter laajensi Schläflin symbolin käyttöaluetta kvasisäännöllisiin monitahokkaisiin lisäämällä symboliin pystysuoran ulottuvuuden. Tämä oli lähtökohtana kehitettäessä yleisempää Coexterin diagrammia. Norman Johnson yksinkertaisti pystysuorien symbolien merkintää ottamalla käyttöön etuliitteen r. Yleisin merkintä on t-merkintä, ja se vastaa suoraan Coexterin diagrammin renkaita. Alternoituja monitahokkaista, joissa on alkuperäisestä monitahokkaasta mukana vain puolet kärjistä, merkitään Coexterin diagrammilla, jossa renkaan sisällä on täplän sijasta aukko, tai Schäflin symbolilla, jonka eteen on lisätty kirjain h. Schäflin symboli, jonka alussa on a, vastaa Coexterin diagrammia, jossa on kaksi tällaista rengasta, ja se tarkoittaa muunnettua monitahokasta, jonka muodostavat molemmat alternoidut monitahokkaat yhteensä. Monitahokkaan pullistaminen (engl. snub) on typistämisen puolinainen muoto, ja holosnub on molempien alternoidun typistämisen tuloksena saatujen monitahokkaiden yhdistelmä.

Form	Schläflin symboli			Symmetria	Coxeterin diagrammi		Esimerkki, {4,3}
Säännöllinen	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$	{p,q}	t0{p,q}	[p,q] tai [(p,q,2)]				Kuutio
Typistetty	${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$	t{p,q}	t0,1{p,q}					Typistetty kuutio
Bitrunkaatio (Typistetty duaali)	${\displaystyle t{\begin{Bmatrix}q,p\end{Bmatrix}}}$	2t{p,q}	t1,2{p,q}					Typistetty oktaedri
Rektifioitu (Kvasisäännöllinen)	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	r{p,q}	t1{p,q}					Kuboktaedri
Birektifikaatio (säännöllinen duaali)	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$	2r{p,q}	t2{p,q}					Oktaedri
Kantellaatio	${\displaystyle r{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	rr{p,q}	t0,2{p,q}					Rombikuboktaedri
Kantitrunkaatio (typistetty rektifioitu)	${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	tr{p,q}	t0,1,2{p,q}					Typistetty kuboktaedri

Alternoitu monitahokas saadaan, kun alkuperäisen monitahokkaan kärjistä joka toinen poistetaan. Coexterin diagrammissa alternaatiota merkitään renkaalla, jonka sisällä ei ole täplää. On kaksi mahdollista tapaa valita, mitkä kärjet alternaatioon otetaan mukaan, mutta symboli ei ilmaise, kummat otetaan mukaan. Jos alternoitu monitahokas vielä alternoidaan toisen kerran, saadaan neljännesmuoto (engl. quarter), joka ilmaistaan merkitsemällä + -merkki renkaan sisään osoittamaan, että on suoritettu kaksi riippumatonta alternaatiota.

Alternaatiot

Muoto	Schläflin symbolit			Symmetria	Coexterin diagrammi		Esimerkki {4,3}
Alternoitu säännöllinen (puolet kärjistä)	${\displaystyle h{\begin{Bmatrix}2p,q\end{Bmatrix}}}$	h{2p,q}	ht0{2p,q}	[1+,2p,q]	=			Puolikuutio (Tetraedri)
Pullistettu säännöllinen	${\displaystyle s{\begin{Bmatrix}p,2q\end{Bmatrix}}}$	s{p,2q}	ht0,1{p,2q}	[p+,2q]
Pullistettu säännöllinen duaali	${\displaystyle s{\begin{Bmatrix}q,2p\end{Bmatrix}}}$	s{q,2p}	ht1,2{2p,q}	[2p,q+]				Pullistettu oktaedri (Ikosaedri)
Alternoitu rektifioitu (p ja q parillisia)	${\displaystyle h{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	hr{p,q}	ht1{p,q}	[p,1+,q]
Alternoitu kahdesti rektifioitu (p ja q parillisia)	${\displaystyle hr{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	hrr{p,q}	ht0,2{p,q}	[(p,q,2+)]
Kvarteroitu (neljäsosa kärjistä jäljellä) (p ja q parillisia)	${\displaystyle q{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	q{p,q}	ht0ht2{p,q}	[1+,p,q,1+]
Pullistettu rektifioitu pullistettu kvasisäännöllinen	${\displaystyle s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	sr{p,q}	ht0,1,2{p,q}	[p,q]+				Pullistettu kuboktaedri (pullistettu kuutio

Alteroiduilla ja holosnuboiduilla muodoilla on Coexterin ryhmän täysi symmetria, ja niitä merkitään kahdella täyttämättömällä renkaalla, mutta ne voivat olla suuremman kuvion osia.

Alteroidut ja holosnuboidut

Muoto	Schläflin symbolit			Symmetria	Coxeterin diagrammi		Esimerkki, {4,3}
Alteroitu säännöllinen	${\displaystyle a{\begin{Bmatrix}p,q\end{Bmatrix}}}$	a{p,q}	at0{p,q}	[p,q]	= ∪			Tähtioktaedri
Holosnubin duaali	ß ${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$	ß{q,p}	at0,1{q,p}	[p,q]				Kahden ikosaedrin yhdistelmä

Merkinnöissä käytetty ß tarkoittaa tässä saksalaista kaksois-s:ää (eszett), ei sitä huomattavasti muistuttavaa kreikkalaisten aakkosten beetaa (β).