Satunnaismuuttuja

Pääartikkeli: Diskreetti satunnaismuuttuja

Alkeistapaukset voidaan koodata satunnaismuuttujiksi käyttämällä yksinkertaisia funktioita. Lantinheitossa perusjoukko on ${\displaystyle \Omega =\{kruuna,klaava\}}$ ja siitä voidaan luoda satunnaismuuttuja ${\displaystyle X}$ määrittelemällä esimerkiksi:

${\displaystyle X(\omega )={\begin{cases}+1,&{\mbox{jos }}\omega {\mbox{ on kruuna}}\\-1,&{\mbox{jos }}\omega {\mbox{ on klaava}}\end{cases}}}$

Toisessa esimerkissä kahden nopan heitossa tulokseksi halutaan molemman nopan silmälukujen summa. Silloin perusjoukon alkeistapaukset muodostuvat noppien silmälukupareista ${\displaystyle (m,n),}$ joista muodostetaan satunnaismuuttuja ${\displaystyle Y}$: ${\displaystyle \{(m,n)\in \Omega |Y(m,n)=m+n\}.}$ Satunnaismuuttujan arvojoukko on silloin ${\displaystyle \{2,3,4,...,12\}.}$ Nämä esimerkit olivat yksinkertaisia satunnaismuuttujia, koska perusjoukko oli kooltaan äärellinen.[2]

Seuraava satunnaismuuttuja muodostuu tapauksista, joita voi olla numeroituvasti ääretön määrä. Heitetään kolikkoa, kunnes saadaan ensimmäisen kerran kruuna. Jos kruuna saadaan heti, merkitään satunnaismuuttujan ${\displaystyle Z}$ arvoksi nolla. Jos saadaan aluksi klaava ja sitten kruuna, merkitään satunnaismuuttujan arvoksi yksi. Satunnaismuuttujan arvojoukko on silloin ${\displaystyle Z=\{0,1,2,3,...\}.}$

Pääartikkeli: Jatkuva satunnaismuuttuja

Esimerkiksi tikanheitto voidaan tulkita jatkuvaksi satunnaisilmiöksi, sillä jokainen osuma seinään ja tauluun voidaan tulkita x-koordinaatiston pisteeksi ${\displaystyle (x,y)\in \Omega }$. Tason pisteitä on nyt ylinumeroituvasti ääretön määrä ja samoin on myös satunnaismuuttujan arvoja. Jos määritellään satunnaismuuttuja ${\displaystyle D}$ siten, että ${\displaystyle D(x,y)={\sqrt {x^{2}+y^{2}}},}$ kun origo on napakympissä, saadaan Borel-joukko niistä ${\displaystyle d}$-säteisistä ympyrälevyistä, missä ${\displaystyle \{D\leq d\}=\{(x,y)\in \Omega |D(x,y)\leq d\}.}$ Satunnaismuuttuja saa silloin arvot ${\displaystyle [0,\infty ).}$ [2]

Satunnaismuuttuja saa yleensä arvot suljetulta väliltä ${\displaystyle [a,b]}$, puoliavoimelta väleiltä ${\displaystyle [a,b)}$ tai ${\displaystyle (a,b]}$ taikka avoimelta väliltä ${\displaystyle (a,b)}$, missä rajat ovat äärellisiä tai äärettömiä.[7]

Kahden nopan silmälukujen summan jakaumafunktion pistetodennäköisyydet jakautuvat kuvaajan mukaisesti.

Todennäköisyysfunktiot ovat diskreetillä ja jatkuvalla satunnaismuuttujilla varsin erilaiset.

Diskreettien satunnaismuuttujien jakauma on luettelo, jossa jokaiseen satunnaismuuttujan arvoon ${\displaystyle X=x_{i}}$ liitetään todennäköisyyden arvo ${\displaystyle p_{i}}$. Usein käytetty merkintätapa on

${\displaystyle P(X=x_{i})=p_{i}.}$

Diskreettien satunnaismuuttujien todennäköisyyksiä kutsutaan myös pistetodennäköisyyksiksi.[6][10]

Esimerkiksi kahden nopan heitossa, jossa satunnaismuuttujana on noppien silmälukujen summa, saadaan satunnaismuuttujan arvojen perusjoukoksi ${\displaystyle \{2,3,4,5,...,10,11,12\}.}$ Kuten oheisesta kuvaajasta voi nähdä, noudavat seuraavat pistetodennäköisyydet sen todennäköisyysjakaumaa: ${\displaystyle P(X=2)\,=P(X=12)={\frac {1}{36}}}$ ja ${\displaystyle P(X=7)={\frac {1}{6}}.}$[10]

Todennäköisyysjakauman todennäköisyyksien summa

${\displaystyle \Sigma p_{i}=1}$

tulee aina olla yksi.[10]

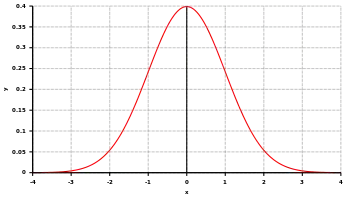
Esimerkki jatkuvasta satunnaismuuttujan tiheysfunktiosta ${\displaystyle \phi (x)}$ on normaalijakauman kuvaaja.

Jatkuvien satunnaismuuttujien todennäköisyysfunktio on tiheysfunktio ${\displaystyle f(x)}$ (joskus ${\displaystyle \phi (x)}$), joka saa satunnaismuuttujan arvoalueella vain positiivisia arvoja ja muualla se saa arvokseen nolla. Se ei voi saada missään negatiivisia arvoja.[7][11]

Todennäköisyys sille, että sattunnaismuuttuja saa arvokseen yli 1,2 eli ${\displaystyle P\{X>1,2\}}$ on kuvaajan väritetyn alueen pinta-ala eli integraali.

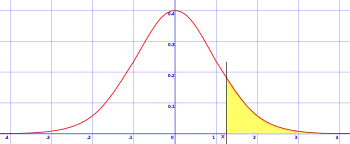
Tiheysfunktion arvot eivät ole todennäköisyyksiä. Jatkuvan satunnaismuuttujan arvot ovat reaalilukuja, joita on yleensä ylinumeroituvasti ääretön lukumäärä. Usein tulkitaankin, että yksittäisen alkeistapauksen satunnaismuuttujan arvon esiintymistodennäköisyys on nolla. Tässä on kuitenkin ristiriita käytännön kanssa. Satunnaismuuttuja antaa tulokseksi joitakin arvoja, joten todennäköisyys voi olla nolla, vaikka tapahtuma olisi teoreettisesti mahdollinen.

Jatkuvan satunnaismuuttujan todennäköisyyksiä lasketaan vain tapahtumille, jotka ovat satunnaismuuttujan arvojen lukuvälejä ${\displaystyle [a,b]}$. Jos b> a, tapahtuman lukuvälissä on ylinumeroituvasti ääretön määrä alkeistapauksia, joiden yhteinen todennäköisyys on äärellinen. Tällä lukuvälillä ${\displaystyle [a,b]}$ otettu tiheysfunktion määrätty integraali onkin todennäköisyyttä merkitsevä numeerinen arvo:

${\displaystyle P(a<X<b)=\int _{a}^{b}f(x)\,dx.}$

Koko tiheysfunktion yli otettu määrätty integraali on aina arvoltaan yksi

${\displaystyle \int _{-\infty }^{+\infty }f(x)\,dx=1,}$

koska sille välille jäävät kaikki alkeistapaukset.

Satunnaismuuttujalla on viisi arvoa välillä ${\displaystyle [a,b]}$, joiden pistetodennäköisyydet ovat kaikki 0,2. Näistä piirretty kertymäfunktio on porrasfunktio, joka on oikealta puolelta jatkuva.

Edellä esitetyn normaalijakauman kertymäfunktion kuvaaja muistuttaa S-käyrää.

Kertymäfunktio eli jakaumafunktio ${\displaystyle F(x)}$ määritellään siten, ettei määrättyä integrointia enää tarvita todennäköisyyksiä laskettaessa. On olemassa useita erilaisia kertymäfunktion määrittelytapoja. Yleisin on kuitenkin määrittää todennäköisyys tapahtumalle, joka sisältää kaikki alkeistapaukset vasemmaltapäin päätearvoon ${\displaystyle x}$ asti. Sekä diskreeteille että jatkuville satunnaismuuttujille tämä tarkoittaa [6][11][12]

${\displaystyle F(x)=P(X\leq x)=\int _{-\infty }^{x}f(t)\,dt.}$

Todennäköisyys tapahtumalle ${\displaystyle [a,b]}$ on silloin laskettavissa ilman määrättyä integrointia

${\displaystyle P(a<X<b)=F(b)-F(a).}$

Kertymäfunktiot ovat kasvavia funktioita, jotka saavat vain arvot

${\displaystyle 0\leq F(x)\leq 1}$.

Diskreeteillä satunnaismuuttujilla kertymäfunktiot ovat porrasfunktioita, jotka kasvavat joka "portaalla". Jatkuvilla satunnaismuuttujilla kuvaaja on yleensä kasvavia ja sileä käyriä. Jos kertymäfunktio on derivoituva, saadaan sen derivaatasta tiheysfunktio

${\displaystyle f(x)={\frac {d\,F(x)}{dx}}.}$