Topologinen aliavaruus

Olkoon ${\displaystyle (X,\tau )}$ topologinen avaruus ja S jokin X:n osajoukko. Olkoon ${\displaystyle \iota :S\hookrightarrow X}$' inkluusio, toisin sanoen sellainen kuvaus, että ${\displaystyle f(x)=x}$ kaikilla ${\displaystyle x\in S}$. Tällöin ${\displaystyle \iota }$:n indusoima topologia joukossa S on ${\displaystyle \{V\cap S\;|\;V\in \tau \}}$, toisin sanoen tässä topologiassa avoimia joukkoja ovat X:n avointen joukkojen ja S:n leikkaukset. Tätä inkluusion indusoimaa topologiaa sanotaan S:n relatiivitopologiaksi jonka S perii X:stä, ja joukkoa S tällä relatiivitopologialla varustettuna X:n aliavaruudeksi.[1]

Vaihtoehtoisesti osajoukon ${\displaystyle S\subset X}$ relatiivitopologia voidaan määritellä karkeimmaksi topologiaksi, jolla inkluusiokuvaus ${\displaystyle \iota :S\hookrightarrow X}$ on jatkuva.

Yleisemmin voidaan olettaa, että ${\displaystyle \iota }$ on mikä tahansa injektio joukosta ${\displaystyle S}$ topologiseen avaruuteen ${\displaystyle X}$. Tällöin S :n relatiivitopologia määritellään karkeimpana topologiana, jossa ${\displaystyle \iota }$ on jatkuva. Avoimia joukkoja tässä topologiassa ovat kaikki muotoa ${\displaystyle \iota ^{-1}(U)}$ olevat joukot, joissa ${\displaystyle U}$ on ${\displaystyle X}$:n avoin osajoukko. Tällöin ${\displaystyle S}$ on homeomorfinen ${\displaystyle X}$:ssä olevan kuvajoukkonsa kanssa, kun tämä joukko on varustettu relatiivitopologialla. Tällaista kuvausta ${\displaystyle \iota }$ sanotaan topologiseksi upotukseksi.

${\displaystyle S}$:n aliavaruutta sanotaan avoimeksi aliavaruudeksi, jos injektio ${\displaystyle \iota }$ on avoin kuvaus, toisin sanoen jos jokaisen ${\displaystyle S}$:n avoimen joukon kuva tässä kuvauksessa on ${\displaystyle X}$:n avoin joukko. Vastaavasti sitä sanotaan suljetuksi aliavaruudeksi, jos ${\displaystyle \iota }$ on suljettu kuvaus.

Merkinnöissä ei joukon ja topologisen avaruuden välillä aina tehdä selvää eroa, mikä saattaa aiheuttaa sekaannusta, kun määritelmiin ensimmäisen kerran tutustutaan. NIinpä jos ${\displaystyle S}$ on ${\displaystyle X}$:n osajoukko ja ${\displaystyle (X,\tau )}$ topologinen avaruus, saatetaan merkintöjä ${\displaystyle S}$ ja ${\displaystyle X}$ käyttää sekä joukoista ${\displaystyle S}$ ja ${\displaystyle X}$ käsitettyinä ${\displaystyle X}$:n osajoukoiksi, että myös avaruuksista ${\displaystyle (S,\tau _{S})}$ ja ${\displaystyle (X,\tau _{X})}$ topologisina avaruuksina edellä kuvatulla tavalla. Niinpä jos esimerkiksi sanotaan, että "${\displaystyle S}$ on ${\displaystyle X}$:n avoin aliavaruus", tarkoitetaan itse asiassa, että ${\displaystyle (S,\tau _{S})}$ on ${\displaystyle (X,\tau _{X})}$:n avoin aliavaruus, toisin sanoen

(i) ${\displaystyle S\in \tau }$, eli S on avoin joukko topologisessa avaruudessa ${\displaystyle X,\tau }$, ja

(ii) ${\displaystyle S}$ on varustettu relatiivitopologialla.

Seuraavassa ${\displaystyle \mathbb {R} }$ tarkoittaa reaalilukujen joukkoa tavanomaisella topologiallaan.

• Luonnollisten lukujen joukon ${\displaystyle \mathbb {N} }$ relatiivitopologia on diskreetti topologia.
• Rationaalilukujen joukon ${\displaystyle \mathbb {Q} }$ relatiivitopologia ei ole diskreetti topologia; esimerkiksi pelkän nollan käsittävä joukko {0} ei ole avoin joukko ${\displaystyle \mathbb {Q} }$:ssa. Jos a ja b ovat rationaalilukuja, avoin väli (a, b) ja ${\displaystyle \mathbb {Q} }$:n leikkaus on myös rationaalilukujen topologiassa avoin ja [a, b] suljettu joukko, mutta jos a ja b ovat irrationaalilukuja, niiden rationaalilukujen joukko, jotka ovat a:n ja b:n välissä, on tässä topologiassa sekä avoin että suljettu joukko.
• Suljettu väli [0,1] on ${\displaystyle \mathbb {R} }$:n aliavaruutena sekä avoin että suljettu, mutta ${\displaystyle \mathbb {R} }$:n osajoukkona se on vain suljettu.
• ${\displaystyle \mathbb {R} }$:n aliavaruutena joukko [0, 1] ∪ [2, 3] muodostuu kahdesta avoimesta osajoukosta (jotka samalla ovat myös suljettuja), ja sen vuoksi se on epäyhtenäinen avaruus.
• Käsitellään puoliavointa väliä S = [0, 1) ${\displaystyle \mathbb {R} }$:n aliavaruutena. Tällöin [0, 1/2) on avoin aliavaruudessa S, mutta ei avaruudessa ${\displaystyle \mathbb {R} }$. Samoin [½, 1) on suljettu S:ssä, mutta ei ${\displaystyle \mathbb {R} }$:ssä. Itsensä osajoukkona S on sekä avoin että suljettu, mutta ei ${\displaystyle \mathbb {R} }$:n osajoukkona.

Relatiivitopologialla on seuraava tyypillinen ominaisuus. Olkoon ${\displaystyle Y}$ avaruuden ${\displaystyle X}$ aliavaruus ja olkoon ${\displaystyle i:Y\to X}$ inkluusiokuvaus. Silloin jokaiselle topologiselle avaruudelle kuvaus ${\displaystyle Z}$: ${\displaystyle f:Z\to Y}$ on jatkuva, jos ja vain jos yhdistetty kuvaus ${\displaystyle i\circ f}$ on jatkuva.

Relatiivitopologian karakteristinen ominaisuus

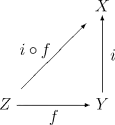
Tämä ominaisuus on karakteristinen siinä mielessä, että sitä voitaisiin käyttää vaihtoehtoisena määritelmänä relatiivitopologialle ${\displaystyle Y}$:ssa.

Relatiivitopologialla on myös seuraavat ominaisuudet. Seuraavassa oletetaan, että ${\displaystyle S}$ on ${\displaystyle X}$:n aliavaruus.

• Jos ${\displaystyle f:X\to Y}$ on jatkuva, sen rajoittuma ${\displaystyle S}$:ään on jatkuva.[2]
• Jos ${\displaystyle f:X\to Y}$ on jatkuva, myös ${\displaystyle f:X\to f(X)}$ on jatkuva.
• Suljettuja joukkoja avaruudessa ${\displaystyle S}$ ovat ${\displaystyle X}$:n suljettujen joukkojen ja ${\displaystyle S}$:n leikkaukset, ja vain ne.
• Jos ${\displaystyle A}$ on ${\displaystyle S}$:n aliavaruus, ${\displaystyle S}$ on myös ${\displaystyle X}$:n aliavaruus ja sellaisena sillä on sama topologia. Toisin sanoen ${\displaystyle A}$ perii ${\displaystyle S}$:stä saman topologian kuin ${\displaystyle X}$:stäkin.
• Olkoon ${\displaystyle S}$ avaruuden ${\displaystyle X}$ avoin aliavaruus (jolloin ${\displaystyle S\in \tau }$). Silloin ${\displaystyle S}$:n osajoukko on avoin ${\displaystyle S}$:ssä, jos ja vain jos se on avoin ${\displaystyle X}$:ssä.
• Olkoon ${\displaystyle S}$ avaruuden ${\displaystyle X}$ suljettu aliavaruus (jolloin ${\displaystyle X\setminus S\in \tau }$). Silloin ${\displaystyle S}$:n osajoukko on suljettu ${\displaystyle S}$:ssä, jos ja vain jos se on suljettu ${\displaystyle X}$:ssä.
• Jos ${\displaystyle B}$ on ${\displaystyle X}$:n topologian kanta, niin ${\displaystyle B_{S}=\{U\cap S:U\in B\}}$ on ${\displaystyle S}$:n topologian kanta
• Metrisen avaruuden osajoukon indusoitu topologia, joka saadaan rajoittamalla metriikka tähän osajoukkoon, on sama kuin saman osajoukon relatiivitopologia aliavaruutena.

Jos siitä, että topologisella avaruudella on jokin topologinen ominaisuus, seuraa, että sama ominaisuus on myös sen kaikilla aliavaruuksilla, ominaisuutta sanotaan perinnölliseksi.[3] Jos ominaisuus on vain suljetuilla osajoukoilla, sitä sanotaan 'heikosti perinnölliseksi.

• Täydellisesti metristyvän avaruuden jokainen avoin ja suljettu aliavaruus on täydellisesti metristyvä.
• Bairen avaruuden jokainen avoin aliavaruus on Bairen avaruus.
• Kompaktin avaruuden jokainen suljettu aliavaruus on kompakti.
• Että avaruus on Hausdorffin avaruus, on perinnöllinen ominaisuus.[4]
• Avaruuden normaalius on heikosti perinnöllinen ominaisuus.[5]
• Että metrinen avaruus on totaalisesti rajoitettu, on perinnöllinen ominaisuus.
• Että avaruus on täysin epäyhtenäinen, on perinnöllinen ominaisuus.
• Että avaruus on N₁-avaruus eli että sen jokaisella pisteellä on numeroituva ympäristökanta, on perinnöllinen kanta.[6]
• Että avaruus on N₂-avaruus eli että sillä on numeroituva kanta, on perinnöllinen ominaisuus.[6]

• Tekijätopologia
• Tulotopologia

• Nicolas Bourbaki: Elements of Mathematics: General Topology. Addison-Wesley, 1966.
• Lynn Arthur Steen, J. Arthur Seebach Jr.: Counterexamples in Topology. Springer-Verlag, 1978. ISBN 978-0-486-68735-3.
• Stephen Willard: General Topology. Dover Publications, 2004. ISBN 0-486-43479-6.