RLC-piiri
RLC-piiri (R, L ja C voivat olla nimessä myös eri järjestyksissä) on virtapiiri, jossa on vastus (R, resistanssi), käämi (L, induktanssi) ja kondensaattori (C, kapasitanssi). RLC-piireissä jännite ja sähkövirta riippuvat niiden taajuudesta.[1][2][3][4] Tämän vuoksi niitä voidaan käyttää sähkötekniikassa ja elektroniikassa esimerkiksi värähtely- eli virityspiireissä ja suodattimissa.

RLC-piireihin liittyviä termejä
Resonanssi
- Pääartikkeli: Resonanssi
RLC-piirit ovat pakotettuja harmonisia värähtelijöitä, eli niiden jännite ja sähkövirta värähtelevät samalla taajuudella kuin piiriin kytketyn sähkölähteen (esimerkiksi generaattori) taajuus.[5] Kondensaattorin ''vaihtovirtavastus'', eli kapasitiivinen reaktanssi on kääntäen verrannollinen jännitteen tai virran muutoksen kulmataajuuteen
kun taas kelan vastaava suure, induktiivinen reaktanssi, on suoraan verrannollinen samaan kulmataajuuteen:
Näin ollen kondensaattori ja kela vastustavat vaihtovirran kulkua eri tavoilla eri kulmataajuuksilla: pienillä kulmataajuuksilla (jännite ja virta muuttuvat hitaasti) kondensaattori vastustaa virran kulkua paljon ja vastaavasti suurilla kulmataajuuksilla (jännite ja virta muuttuvat nopeasti) kela vastustaa virran kulkua paljon. Vastuksen resistanssi ei juurikaan[Huom. 1] riipu kulmataajuudesta, joten resistanssin vaikutus sähkövirran suuruuteen on taajuuden suhteen vakio. Piiristä riippuvalla tietyllä kulmataajuudella piirin impedanssi siis saavuttaa maksimi- tai minimiarvonsa. Tätä kulmataajuutta vastaavaa taajuutta
sanotaan ko. piirin resonanssitaajuudeksi.[12][13][14][15] Sekä sarjaan- että rinnankytkettyjen RLC-piirien resonanssikulmataajuus on
missä
- on kelan induktanssi ja
- on kondensaattorin kapasitanssi.
Kaistanleveys
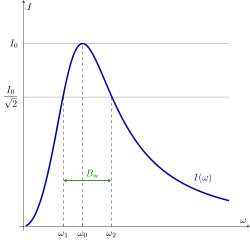
Piirissä kuluva pätöteho riippuu sähkövirran suuruudesta, joka puolestaan riippuu sähkövirran taajuudesta. Piirin keskimääräinen pätöteho on
,[17]
missä
- on vaihtojännitteen huippuarvo ja
- on piirin resistanssi.
Sarjaresonanssipiiri
Sarjaresonanssipiirissä pätöteho on maksimissaan, kun piiri värähtelee resonanssissa. Resonanssitaajuudella , jolloin piirin pätöteho saavuttaa maksimiarvonsa. Tietyllä resonanssitaajuutta pienemmällä ja suuremmalla taajuudella piirin teho puolittuu resonanssitilanteesta. Ts. on olemassa kulmataajuusalue siten, että
,
kun . Desibeliasteikolla tehon puolittuminen tarkoittaa sitä, että tehon muutos on −3 dB.[18] Rajakulmataajuuksien erotusta sanotaan piirin kaistanleveydeksi:
Kaistanleveys voidaan laskea kulmataajuuksien sijaan myös taajuuksilla, sillä :
.
Toisinaan on tarpeen määritellä myös suhteellinen kaistanleveys, joka on kaistanleveyden ja resonanssitaajuuden tai -kulmataajuuden suhde:
tai .[18]
Hyvyysluku
- Pääartikkeli: Hyvyysluku
RLC-piirin hyvyysluku kertoo piiriin varastoituneen energian ja yhden jakson aikana hyödyntämättömään muotoon (mm. lämmöksi) muuttuvan energian suhteesta.[17][19] Hyvyysluku on piirin induktiivisen reaktanssin ja resistanssin suhde resonanssissa:
Hyvyysluku kertoo piirin käyttäytymisestä resonanssitaajuuden ympäristössä: mitä suurempi hyvyysluku on, sen kapeampi piirin taajuuskaista on. Kaistanleveyttä voidaan siis pienentää kasvattamalla piirin resistanssia.[17][20] Pienillä taajuuksilla tämä on kuitenkin käytännössä mahdotonta, sillä rautasydämisenkin käämin induktanssi−resistanssi-suhde on luokkaa 0,05 henryä per ohmi. Näin ollen käytännössä
.[17]
Hyvyysluku on piirin suhteellisen kaistanleveyden käänteisluku:
Sarjaan kytketty RLC-piiri

RLC-piiri voidaan toteuttaa esimerkiksi siten, että vastus, käämi ja kondensaattori on kytketty peräkkäin sarjaan. Tällöin Kirchhoffin virtalain mukaisesti kaikkien komponenttien läpi kulkee sama sähkövirta. Piirin aikariippuvuutta kuvaa tällöin differentiaaliyhtälö
,[21]
missä
- on jännitteen hetkellinen arvo,
- on sähkövirran hetkellinen arvo ja
- on kondensaattorin hetkellinen sähkövaraus.
Tästä differentiaaliyhtälöstä voidaan ratkaista piirin hetkellinen sähkövirta ajan funktiona:
,
missä on jännitteen huippuarvo ja

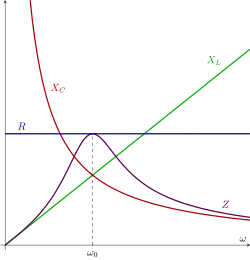
on piirin sähkövirran ja jännitteen välinen vaihe-ero.[21] Sarjaan kytketyn RLC-piirin impedanssi voidaan ilmoittaa joko kompleksilukuna
tai itseisarvonsa avulla
Kun sähkövirran taajuus on sama kuin piirin resonanssitaajuus,
,
kutsutaan piiriä sarjaresonanssiksi.[15][16][21] Resonanssissa käämin ja kondensaattorin jännitteet ovat yhtä suuret, mutta ne ovat vastakkaisissa vaiheissa, joten ne kumoavat toisensa. Näin ollen sarjaresonanssipiirin impedanssi koostuu puhtaasti resistanssista () ja sähkövirta saavuttaa maksimiarvonsa:
Rinnan kytketty RLC-piiri
Toinen verrattain yksinkertainen RLC-piiri on piiri, jossa vastus, käämi ja kondensaattori on kytketty vierekkäin eli rinnan (ks. kuva Kytkentä A)[15][23] tai jossa pelkästään käämi ja kondensaattori ovat rinnan ja vastus näiden kanssa sarjassa (ks. kuva Kytkentä B)[13]. Resonanssitaajuudella näitä kumpaakin piiriä kutsutaan rinnakkaisresonanssiksi.[13][15][23]
Vastus, käämi ja kondensaattori rinnan

Kytkentää, jossa vastus, käämi ja kondensaattori ovat kaikki rinnan jännitelähteen kanssa, kutsutaan myös GLC-piiriksi,[24] missä G tarkoittaa vastuksen konduktanssia
.
Rinnan kytketyn RLC-piirin impedanssille pätee
,
mutta sarjakytkennälle analogisten yhtälöiden saavuttamiseksi voidaan käyttää admittanssia ja konduktanssia:
.[23]
Impedanssi itseisarvona on tällöin
.
Kun sähkövirran kulmataajuus on sama kuin piirin resonanssikulmataajuus
,
ovat käämin ja kondensaattorin läpi kulkevat sähkövirrat yhtä suuret, mutta vastakkaisissa vaiheissa. Tällöin rinnakkaisresonanssipiirin impedanssi koostuu puhtaasti resistanssista () ja sähkövirta saavuttaa minimiarvonsa:
.[15]
Käämi ja kondensaattori rinnan

Kytkentä, jossa käämi ja kondensaattori ovat rinnan ja vastus näiden kanssa sarjassa jännitelähteen kanssa, on myös värähtelypiiri, jolla havaitaan resonanssi-ilmiö.[13] Tämän kytkennän impedanssi on
.[13]
Itseisarvona impedanssi on tällöin
.
Kun sähkövirran kulmataajuus on sama kuin piirin resonanssikulmataajuus
,

kasvaa impedanssi äärettömän suureksi (). Tällöin rinnakkaisresonanssipiirin sähkövirta saavuttaa minimiarvonsa, joka on nolla.[13]
RLC-suodattimet
- Pääartikkeli: Elektroniikan suodattimet
Yleisesti RLC-piiriä sanotaan toisen kertaluvun suodattimeksi.[25] Ohessa RLC-piiri kytkettynä erilaisiksi suodattimiksi
- RLC-suotimia
 Kaistanpäästösuodin.
Kaistanpäästösuodin. Kaistanestosuodin.
Kaistanestosuodin. Alipäästösuodin.
Alipäästösuodin.
Kaistanpäästösuodatin
Kaistanpäästösuodatin tai -suodin on elektroninen suodatin, jonka tehtävänä on päästää lävitseen tietyn taajuusalueen sähköiset signaalit ja heikentää tämän taajuusalueen ulkopuolisia signaaleja. Tämä voidaan toteuttaa esimerkiksi sarjaresonanssipiirillä, jonka komponentit valitaan siten, että piirin resonanssitaajuus on sama kuin haluttu suodatetun signaalin taajuus.[24] Kun vaihtojännitteen taajuus sisääntulossa (in) on lähellä piirin resonanssitaajuutta, on piirin impedanssi pienimmillään. Muun taajuuden signaalit suodattuvat sitä tehokkaammin, mitä kauempana ne ovat resonanssitaajuudesta. Kaistanleveys on valittava siten, että päästettävä signaali mahtuu suodattimen taajuuskaistaan.
Kaistanestosuodin
Kaistanestosuodatin tai -suodin on elektroninen suodatin, jonka tehtävänä on estää tietyn taajuusalueen sähköiset signaalit ja vahvistaa tämän taajuusalueen ulkopuolisia signaaleja. Tämä voidaan toteuttaa esimerkiksi rinnakkaisresonanssipiirillä, jonka komponentit valitaan siten, että piirin resonanssitaajuus on sama kuin haluttu estettävän signaalin taajuus.[24] Kun vaihtojännitteen taajuus sisääntulossa (in) on lähellä piirin resonanssitaajuutta, on piirin impedanssi suurimmillaan. Muun taajuiset signaalit pääsevät läpi sitä tehokkaammin, mitä kauempana ne ovat resonanssitaajuudesta. Kaistanleveys on valittava siten, että estettävä signaali mahtuu suodattimen taajuuskaistaan.
Alipäästösuodin
Alipäästösuodin vaimentaa signaalista rajataajuutta korkeammat taajuudet. Sen taajuusvaste kulmataajuuden funktiona on[25]
,
mistä nähdään, että suodin on toista kertalukua. Piiri ei "resonanssitaajuudellakaan" korosta resonanssitaajuutta, jos Q <= 1.
Katso myös
Lähteet
Viitteet
- Brophy, James J.: ”AC-Circuit Analysis”, Basic Electronics for Scientists. 5. painos. Singapore: McGraw-Hill, 1990. ISBN 0-07-100675-3. (englanniksi)
- Grant, I. S. & Phillips, W. R.: ”Alternating currents and transients”, Electromagnetism. 2. painos. John Wiley & Sons, Ltd, 1990. ISBN 978-0-471-92711-9. (englanniksi)
- Knight, Randall D.: ”AC Circuits”, Physics for Scientists and Engineers, A Strategic Approach with Modern Physics. 3. painos. Pearson, 2014. ISBN 978-1-292-02078-5. (englanniksi)
- Ahoranta, Jukka: ”Vaihtosähköpiirit”, Sähkötekniikka. 14., uudistettu painos. Helsinki: Sanoma Pro, 2015. ISBN 978-952-63-1570-6.
- Knight, s. 1158
- Brophy, s. 38
- Knight, s. 1161
- Ahoranta, s. 138
- Brophy, s. 41
- Knight, s. 1165
- Ahoranta, s. 143
- Grant & Phillips, s. 268−269
- Brophy, s. 139−142
- Knight, s. 1168
- Ahoranta, s. 163−165, 170−175
- Tarkka, Pentti & Hietalahti, Lauri: Piirianalyysi 2, s. 180, 190. 2. tarkistettu painos. Helsinki: Edita Publishing Oy, 2006. ISBN 951-37-3926-0.
- Grant & Phillips, s. 270−273
- Tarkka & Hietalahti, s. 185−189
- Tarkka & Hietalahti, s. 184−185, 194
- Brophy, s. 145
- Brophy, s. 137−139
- Knight, s. 1167
- Tarkka & Hietalahti, s. 189−193
- Tarkka & Hietalahti, s. 199−202
- K. Webb: ENGR 202 – Electrical Fundamentals II, SECTION 3: SECOND-ORDER FILTERS web.engr.oregonstate.edu. Viitattu 21.3.2022.
Huomautukset
- Suurilla taajuuksilla johtimissa havaitaan nk. virranahtoilmiö, joka aiheuttaa resistanssin kasvun varauksenkuljettajien ahtautuessa johtimen pinnoille. [Grant & Phillips, s. 390]
Aiheesta muualla
 Kuvia tai muita tiedostoja aiheesta RLC-piiri Wikimedia Commonsissa
Kuvia tai muita tiedostoja aiheesta RLC-piiri Wikimedia Commonsissa