Pyörähdyspinta

Yksinkertaisimpia pyörähdyspintoja ovat lieriö- ja kartiopinnat, jotka saadaan, kun suora tai jana pyörähtää jonkin akselin ympäri. Tällöin tuloksena on lieriö, jos pyörähtävä suora tai jana on yhden­suuntainen akselin kanssa, muussa tapauksessa kartio. Kun ympyrä pyörähtää jonkin halkaisijansa ympäri, tuloksena on aina pallo­pinta, jossa alku­peräinen ympyrä on isoympyränä. Sen sijaan jos ympyrä pyörähtää sellaisen akselin ympäri, joka ei kulje ympyrän sisään jäävän alueen eli kiekon kautta, tuloksena on toruspinta, joka ei leikkaa itseään.

Pyörähdspinnan ja sellaisen tason leikkauksia, johon sen akseli kuuluu, sanotaan meri­dio­naali­siksi leikkauksiksi. Jokaista meri­dio­naa­lista leikkausta voidaan pitää pinnan genera­trixina leikkauksen ja akselin määrittämässä tasossa.[2]

Pyörähdyspinnan ja sen akselia vastaan kohtisuorien tasojen leikkaukset ovat ympyröitä. Pyörähdyspinnan ja kahden tällaisen tason rajoittama kappale on pyörähdyskappale.

Jotkin hyperboloidit, laskettiinpa mukaan sen molemmat haarat tai vain toinen niistä, sekä jotkin elliptiset paraboloidit ovat pyörähdys­pintoja. Sellaisia ovat ne toisen asteen pinnat, joiden poikki­leikkaus akselia vastaan kohti­suorassa suunnassa on ympyrä.

Jos generatrix on jonkin funktion ${\displaystyle y=f(x)}$ kuvaaja ja tämä pyörähtää x-akselin ympäri, pyörähdys­pinnan käsittävät ne avaruuden pisteet (x, y, z), joiden etäisyys x-akselista on f(x) eli jotka toteuttavat yhtälön:

${\displaystyle f(x)^{2}=y^{2}+z^{2}}$.[3]

Jos pyörähtävällä käyrällä on parametriesitys ${\displaystyle (x(t),y(t))}$, missä t vaihtelee jollakin välillä ${\displaystyle [a,b]}$ ja pyörähdys­akselina on y-akseli, pyörähdys­pinnan pinta-ala A_y voidaan laskea integraalilla

${\displaystyle A_{y}=2\pi \int _{a}^{b}x(t)\,{\sqrt {\left({dx \over dt}\right)^{2}+\left({dy \over dt}\right)^{2}}}\,dt,}$

edellyttäen, että x(t) ei päätepisteiden a ja b välillä saa missään negatiivisia arvoja. Tämä lauseke seuraa Pappuksen sentroidilauseesta.[4] Tässä esiintyvä lauseke

${\displaystyle {\sqrt {\left({dx \over dt}\right)^{2}+\left({dy \over dt}\right)^{2}}}}$

seuraa Pythagoraan lauseesta ja esittää käyrän kaaren pienintä osuutta samoin kuin kaaren­pituuden kanssa. Lauseke ${\displaystyle 2\pi x(t)}$ on sen matkan pituus, jonka tämä käyrän osa kulkee käyrän pyörähtäessä, kuten Pappuksen lause edellyttää.

Samaan tapaan jos pyörähdys­akselina on x-akseli eikä lauseke ${\displaystyle y(t)}$ saa missään negatiivisia arvoja, pyörähdys­pinnan ala on[5]

${\displaystyle A_{x}=2\pi \int _{a}^{b}y(t)\,{\sqrt {\left({dx \over dt}\right)^{2}+\left({dy \over dt}\right)^{2}}}\,dt.}$

Jos käyrä voidaan esittää funktiolla ${\displaystyle y=f(x),a\leq x\leq b}$, integraali yksinkertaistuu muotoon

${\displaystyle A_{x}=2\pi \int _{a}^{b}y{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}\,dx=2\pi \int _{a}^{b}f(x){\sqrt {1+{\big (}f'(x){\big )}^{2}}}\,dx}$[3]

kun käyrä pyörähtää x-akselin ympäri, ja muotoon

${\displaystyle A_{y}=2\pi \int _{a}^{b}x{\sqrt {1+\left({\frac {dx}{dy}}\right)^{2}}}\,dy}$

kun se pyörähtää y-akselin ympäri ja a ≤ y ≤ b.

Esimerkiksi yksikköpallo saadaan, kun yksikköympyrä eli käyrä ${\displaystyle y(t)=\sin {t},x(t)=\cos {t}}$, missä t on välillä [0,π], pyörähtää x-akselin ympäri. Sen pinta-ala on siis

${\displaystyle {\begin{aligned}A&{}=2\pi \int _{0}^{\pi }\sin(t){\sqrt {{\big (}\cos(t){\big )}^{2}+{\big (}\sin(t){\big )}^{2}}}\,dt\\&{}=2\pi \int _{0}^{\pi }\sin(t)\,dt\\&{}=4\pi .\end{aligned}}}$

Yleisemmin ympyrällä, jonka säde on r, on parametri­esitys ${\displaystyle y(x)={\sqrt {r^{2}-x^{2}}}}$. Kun se pyörähtää x-akselin ympäri, syntyy pallopinta, jonka ala on

${\displaystyle {\begin{aligned}A&{}=2\pi \int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,{\sqrt {1+{\frac {x^{2}}{r^{2}-x^{2}}}}}\,dx\\&{}=2\pi r\int _{-r}^{r}\,{\sqrt {r^{2}-x^{2}}}\,{\sqrt {\frac {1}{r^{2}-x^{2}}}}\,dx\\&{}=2\pi r\int _{-r}^{r}\,dx\\&{}=4\pi r^{2}\,\end{aligned}}}$

Minimaalinen pyörähdyspinta on kahden pisteen välisten käyrien määrittämistä pyörähdys­pinnoista se, jonka pinta-ala on pienin eli joka minimoi pinta-alan.[6] Yksi variaatiolaskennan keskeisimmistä tehtävistä on löytää kahden pisteen välisistä käyristä se, joka tuottaa minimaalisen pyörähdyspinnan.[6]

Ainoat minimaaliset pyörähdys­pinnat ovat taso ja katenoidi.[7]

Minkä tahansa skalaari­funktion ${\displaystyle y=f(x)}$ kuvaajaa vastaava pyörähdys­pinta voidaan muodostaa asettamalla u funktion parametriksi ja samalla pyörähdys­akselin funktioksi ja pyöräyttämällä funktio akselin ympäri v:n avulla valitsemalla kahdeksi muuksi funktioksi ${\displaystyle f(u)\sin {v}}$ ja ${\displaystyle f(u)\cos {v}}$ Esimerkiksi funktion ${\displaystyle y=f(x)}$ kuvaaja voidaan pyöräyttää x-akselin ympäri aloittamalla xz-tason ylä­puolelta ja para­metroimalla se

${\displaystyle {\vec {r}}(u,v)=\langle u,f(u)\sin v,f(u)\cos v\rangle }$

missä ${\displaystyle u=x}$ ja ${\displaystyle v\in [0,2\pi ]}$.

Geodesian pyörähdyspinnalla määrittää Clairaut'n relaatio.

Neliön generoima toroidi

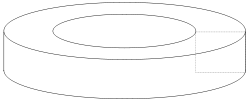
Pyörähdys­pintaa, jonka rajoittamassa kappaleessa on reikä ja jonka pyörähdys­akseli ei leikkaa pintaa, sanotaan toroidiksi.[8] Esimerkiksi kun suorakulmio pyörähtää sen jomman­kumman sivun suuntaisen, mutta kokonaan suora­kulmion ulko­puolella olevan akselin ympäri, syntyy ontto rengas, jonka poikki­leikkaus on suora­kulmainen. Jos pyörähtävä käyrä on ympyrä, syntyvää toroidia sanotaan torukseksi.

Pyörähdys­pinnoilla on keskeinen merkitys monilla fysiikan ja insinööri­tieteiden aloilla. Kun kappaleita kuvataan digitaalisesti, pyörähdys­kappaleita voidaan usein käyttää pinta-alojen määrittämiseen tarvitsematta mitata kuvattavan kappaleen pituutta ja sädettä.

• Pyörähdyskappale
• Gabrielin torvi
• Pintaintegraali

• Kivelä, Simo K.: Algebra ja geometria. Espoo: Otatieto, 1989. ISBN 951-672-103-6.

• Surface of Revolution Wolfram MathWorld. Viitattu 23.9.2016. (englanniksi)
• Surface de révolution Encyclopédie des Formes Mathématiques Remarquables. Viitattu 23.9.2016. (ranskaksi)