Lineaarinen funktio
Lineaarinen funktio on polynomifunktio, jonka asteluku on 1. Sen yleinen matemaattinen lauseke voidaan esittää muodossa
missä a on kulmakerroin ja b vakio. Funktion nimessä lineaarinen viittaa kuvaajan muotoon, joka on suora. Lineaarisia funktioita käytetään matemaattisessa mallinnuksessa talouden, tieteen ja tekniikan aloilla. Niillä on polynomifunktioiden oheella merkittävä rooli matematiikan kouluopetuksessa eri maissa.
Erikoistapaukset
Lineaarisella funktiolla on kolme erikoistapausta riippuen sen parametrien arvoista.
- Kun a = 0, saadaan , koska . Tätä kutsutaan vakiofunktioksi ja se saa kaikilla x:n arvoilla saman vakioarvon b. Vakiofunktion erikoistapaus on nollafunktio, jonka arvoksi tulee aina nolla (ei mitään).
- Kun a ≠ 0 ja b = 0, saadaan , koska . Silloin funktion arvo f(x) ja muuttuja x ovat suoraan verrannolliset eli . Jos funktion kerroin a = 1, saadaan . Funktio on tällöin identiteettifunktio, jolla funktion f(x) arvo on sama kuin muuttujan x arvo.
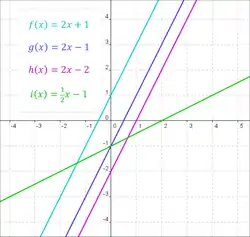
 Vakiofunktioiden kuvaajia. |
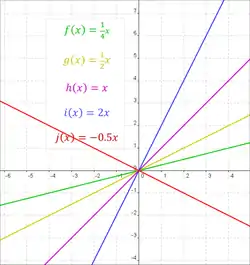 Suoraan verrannollisten funktioiden kuvaajia. |
Kun vakiotermi , niin lineaarinen funktio on pariton funktio [1][2]
Tapauksessa funktio on vakiofunktiona parillinen funktio.
Funktion yleisiä ominaisuuksia
Monotonisuus
Lineaarinen funktio on aidosti monotoninen. Funktio on aidosti kasvava, kun kulmakerroin ja aidosti vähenevä, kun .
Vakiofunktiolla ja sen kuvaaja kulkee vaakasuoraan. Tällöin funktio on vain monotoninen. Se voidaan tulkita sekä kasvavaksi että väheneväksi funktioksi.
Käänteisfunktio
Koska lineaarinen funktio on monotoninen, on sillä olemassa käänteisfunktio. Ainoa poikkeus säännöstä on vakiofunktio, jolla ei ole käänteisfunktiota. Funktion
käänteisfunktio voidaan muodostaa
Derivaatta ja integraali
Yleisen lineaarisen funktion derivaattafunktio [3] on vakiofunktio
- .
Välillä lineaarisen funktion f(x) kuvaajan ja x-akselin väliin jäävän alueen pinta-alan A voi laskea puolisuunnikassäännöllä tarkasti ilman integrointia [5]
Lineaarinen funktio mallinnuksessa
Lineaarinen funktiota käytetään lineaarisessa mallinnuksessa, jolla approksimoidaan kohdefunktiota. Se on samalla yksi huonoimpia malleja, sillä se huomioi kohdefunktion ominaisuuksia minimaalisesti, mutta toisaalta se on nopea laskea. Siksi se on suosittu valinta tietokonesimulaatioissa. Funktion parametrit a,b valitaan siten, että funktio kuvaa kohdefunktiota hyvin. Parametrien valintatapoja on erilaisia.
Korrelaatiosuora
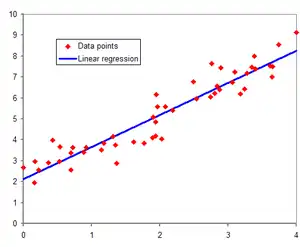

Kohdefunktion tunnettuja arvoja voi approksimoida lineaarisella funktiolla, jonka kertoimet a,b määritetään regressioanalyysillä käyttäen pienimmän neliösumman menetelmällä [6]. Kohdefunktion arvojen ja lineaarisen funktion arvojen vastaavuutta voidaan mitata korrelaatiokertoimella. Jos korrelaatiokerroin on 1, on myös kohdefunktion arvot lineaarisesti riippuvia muuttujastaan x ja niiden kautta voidaan piirtää suora. Jos korrelaatiokerroin on alle 1, ei lineaarinen funktio kuvaa kohdefunktion arvoja tarkasti.[7]
Kohdefunktion lauseketta ei tarvitse tällä menetelmällä tuntea. Riittää, että tietää riittävästi (x,f(x))-pareja, joiden kulkua approksimoidaan tilastollisesti.[8]
Lineaarinen interpolaatio
Kohdefunktio voidaan korvata lineaarisella funktiolla, joka approksimoi sitä hyväksyttävällä virheellä. Yksinkertaiseen interpolointiin tarvitaan kaksi kohdefunktion arvoa kohdista a ja b, joiden avulla lasketaan arvoparit (a,f(a)) ja (b,f(b)). Arvoparien kautta sovitetaan suora, jonka kulku voidaan esittää lineaarisena funktiona g(x):
Lineaarinen funktio muodostamista kahden pisteen avulla kutsutaan myös Lagrangen interpolaatiopolynomi-menetelmäksi ja saatua suoraa saatetaan kutsua myös sekantiksi.
Moniosainen interpolointi suoritetaan siten, että kohdefunktion määrittelyalue jaetaan useaan osaväliin, joiden päätepisteissä määritetään kohdefunktion arvot. Sitten muodostetaan murtoviiva, joka kulkee päätepisteiden kautta ja ilmaistaan tämä paloittaisen funktiona.[9]
Lähteet ja viitteet
- Wolfram Mathwolrd: Odd functions
- PurpleMath: Even and Odd functions
- Jyväskylän yliopisto: Derivoimissääntöjä
- Jyväskylän yliopisto: Integroimissääntöjä
- Riekkinen, Tuomo: Puolisuunnikassääntö (Arkistoitu – Internet Archive)
- Ilmatieteen laitos: Tilastotiede datan prosessoinnissa
- Kuopion yliopisto: Pienimmän neliösumman menetelmä ja Graafin tekeminen, ss. 8-11 (Arkistoitu – Internet Archive)
- Joensuun yliopisto: Suoran sovitus pistejoukkoon[vanhentunut linkki]
- Riekkinen Tuomo: Lineaarinen interpolaatio[vanhentunut linkki]
Kirjallisuutta
- Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf). Viitattu 8.7.2019.