Laajennettu reaalilukujoukko

Laajennettu reaalilukujoukko on lukujoukko, joka saadaan lisäämällä reaalilukujoukkoon $\mathbb {R}$ kaksi uutta elementtiä: positiivinen äärettömyys +∞ eli ∞ ja negatiivinen äärettömyys −∞. [1] [2] Laajennettua reaalilukujoukkoa voidaan merkitä symbolilla ${\overline {\mathbb {R} }}$ tai välinä [−∞, +∞]. Laajennetun reaalilukujoukon geometrinen vastine on laajennettu lukusuora, jossa ajatellaan tavallisen lukusuoran kumpaankin päähän lisätyksi yksi äärettömän kaukainen piste.

Ylin reaalilukusuora on laajennettu siten, että mukaan on otettu luvut

\infty

ja

-\infty

ja ne ovat lukusuoran päätepistetitä. Alempi kuvio liittyy toiseenn laajennustulkintaan.

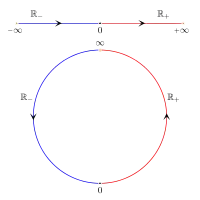
Laajennettu reaalilukujoukko on tarpeellinen erityisesti raja-arvotarkasteluissa ja mittateorian sovelluksissa.

Laskutoimitukset

Tavalliset reaalilukujen laskutoimitukset voidaan osittain ottaa käyttöön myös laajennetussa reaalilukujoukossa.

{\begin{aligned}a+\infty =+\infty +a&=+\infty ,&a&\neq -\infty \\a-\infty =-\infty +a&=-\infty ,&a&\neq +\infty \\a\cdot \pm \infty =\pm \infty \cdot a&=\pm \infty ,&a&\in (0,+\infty ]\\a\cdot \pm \infty =\pm \infty \cdot a&=\mp \infty ,&a&\in [-\infty ,0)\\{\frac {a}{\pm \infty }}&=0,&a&\in \mathbb {R} \\{\frac {\pm \infty }{a}}&=\pm \infty ,&a&\in \mathbb {R} ^{+}\\{\frac {\pm \infty }{a}}&=\mp \infty ,&a&\in \mathbb {R} ^{-}\end{aligned}}

Näissä määrittelyissä a + ∞ on sekä a + (+∞) että a − (−∞), ja vastaavasti a − ∞ on sekä a − (+∞) että a + (−∞).

Sen sijaan ∞−∞, ±∞ ÷ ±∞, (±∞)⁰, 0^±∞, 1^±∞ ja (−∞)^±∞ ei tavallisesti ole määritelty. Raja-arvolaskennassa määrittämätön 0 * ±∞ taas määritetään todennäköisyyslaskennassa ja mittateoriassa tavallisesti nollaksi.

Lähteet

Metsänkylä, Tauno & Näätänen, Marjatta: Algebra s. 143 matematiikkalehtisolmu.fi. 2010. Viitattu 8.7.2019.
Suominen, Kalevi & Vala, Klaus: Topologia, s. 86. Gaudeamus, 1965. ISBN 951-662-050-7.

Kirjallisuutta

Rikkonen, Harri: Matematiikan pitkä peruskurssi II: Reaalimuuttujan funktioiden differentiaalilasku. Helsinki: Otakustantamo, 1969. ISBN 951-671-022-0.
Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[m1-1] Metsänkylä, Tauno & Näätänen, Marjatta: Algebra s. 143 matematiikkalehtisolmu.fi. 2010. Viitattu 8.7.2019.

[s1-2] Suominen, Kalevi & Vala, Klaus: Topologia, s. 86. Gaudeamus, 1965. ISBN 951-662-050-7.