Lähimmän naapurin interpolaatio

Lähimmän naapurin interpolointimenetelmä (engl. Nearest-neighbor interpolation) on yksinkertainen monimuuttujainen interpolointimenetelmä. Näytteet sijaitsevat yksi- tai moniulotteisissa pisteissä, joiden etäisyydet arvioitavaan kohtaan voidaan määrittää. Etäisyys voi olla joko euklidinen etäisyys tai jokin muu etäisyysfunktion arvo, joka noudattaa metriikan perusteita. Kunkin kohdan arvo saadaan lähimmän näytteen arvosta.[1]

Lähimmän naapurin interpolointi tuottaa yhden muuttujan tapauksessa askelfunktion kuvaajan.
Tasossa lähimmän naapurin interpolointi tuottaa erikokoisia näytteitä ympäröiviä alueita, joissa on kussakin sama arvo kuin näytteessä (kuvassa sama väri).
Mikäli näytteet sijaitsevat hilamaisesti järjestäytyneinä, ovat syntyneet näytteen lähiympäristöt suorakulmion muotoisia.

Menetelmällä voi interpoloida spatiaalisesti myös sellaista dataa, joka ei ole numeerisesti käsiteltävissä. Tällainen luokka-asteikkoa toteuttava data on esimerkiksi metsän puulajit tai digitaalisen valokuvan väripikselit. Menetelmän heikkouksia ovat riippuvuus vain yhden näytteen arvosta, näytteiden välisen vuorovaikutksen huomiotta jättäminen, näytteiden keskinäisen sijoittelun vaikutuksesta alueen laajuuteen ja reuna-alueen vaikutuksen laajasta kantamasta.[1]

Menetelmä ei ole sama kuin engl. nearest neighbour weighted interpolation, jonka toinen nimi on engl. inverse distance method eli "käänteisen etäisyyden menetelmä".[2]

Esimerkkejä

Yksiulotteinen tapaus

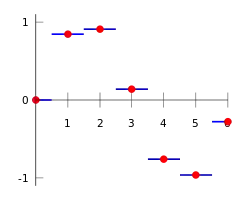
Funktiosta tunnetaan arvot vain muutamassa kohdassa, joiden väliin halutaan estimoida puuttuvia arvoja. Tällöin mitataan etäisyydet kaikkiin pisteisiin ja valitaan se piste, joka on lähinnä estimoitavaa kohtaa. Kohtaan interpoloidaan eli annetaan arvoksi kyseisen näytteen arvo. Menetelmän seurauksena syntyy interpolaatiokuvaaja, jossa lasketut arvot ovat vakioita kunkin näytteen ympäristössä. Interpolaatio vaihtaa tuottamansa arvon, kun joudutaan lähelle muuta näytettä. Tämä tapahtuu aina vierekkäisten näytteiden puolivälissä.

Kaksiulotteinen tapaus

Funktiosta tunnetaan arvot joissakin pisteissä, jotka sijaitsevat eri puolilla tasoa. Kun lasketaan interpoloitava arvo tason pisteessä, lasketaan etäisyydet kuhunkin näytteeseen ja valitaan arvoksi lähimmän näytteen arvo. Kunkin näytteen lähiympäristössä on kaikissa pisteissä sama arvo kuin näytteessä.[1]

Lähiympäristön muoto riippuu käytettävästä etäisyyden metriikasta. Jos käytetään etäisyyteen tavallista euklidisen geometrian etäisyyttä, muuttuvat interpoloitavat arvot aina kahden näytteen puolivälissä ja arvojen välinen raja on aina suoraviivainen. Tämä voidaan piirtää geometrisesti siten, että kahden lähimmän näytteen lähiympäristön raja on näytteitä yhdistävän janan keskinormaalilla. Kun piirretään yhden näytteen keskinormaalit lähinaapureidensa kanssa, rajaavat ne konveksin monikulmion. Tällaisten alueiden mosaiikkia kutsutaan Voronoin polygoneiksi (eli Thiessen-polygonit ja Dirichlet-solut). Jos näytteiden sijainnit muodostavat suorakulmaisen hilamaisen rakenteen, muotoutuvat Voronoin polygonit suorakulmioiksi.[1][3]

Valokuvien suurentaminen ja pienentäminen

Digitaalivalokuvien suurentamisessa, jossa kuvapikselien väliin lisätään uusia pikseleitä, käytetään yhtenä interpolaatiomenetelmänä tätä nopeaa lähimmän naapurin menetelmää. Pienennettäessä valokuvia voidaan jättää pikseleitä samalla menetelmällä valitsemalla jokin reunapiste uuden pisteen väriarvoksi. Lisättävien uusien pikselien väri- ja kirkkausarvot on mahdollista kopioida viereisistä pikseleistä tiettyyn rajaan asti. Suuret suurennokset aiheuttavat valokuvien sisälle sahalaitaisuutta tai virheiksi tulkittavia jälkiä sekä myös pehmentymistä ja sumenemista. Menetelmä on kuitenkin eräs nopeimmista valokuvien muunnosalgoritmeista.[4][5][6][7]

Kuvia

Seuraavista kuvista voi nähdä eron eri etäisyysfunktioiden vaikutuksista näytteiden lähiympäristön rajoihin.

Pieni valokuva, jonka koko on 40×40 pikseliä, koko nelinkertaistettiin ja siihen lisätyt pikselit interpoloitiin lähimpien naapureiden pikselien väreillä.

-->

Sana "Wiki" on renderöity 109 pikselin levyiseksi ja sen jälkeen kuvaa kasvatettiin 218 pikselin levyiseksi interpoloimmalla välit lähimmän naapurin menetelmällä.

-->

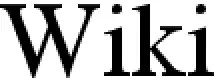
Lähteet
  1. Huhtinen, Markus: Deterministiset interpolointimenetelmät, Pohjois-Karjalan AMK, 2003
  2. Bourke, Paul: Interpolation methods, 1999
  3. Iehias: Spatial interpolation and extrapolation methods
  4. Markelin, Lauri: Geometriset muunnokset; interpolointimenetelmien vertailua, Helsingin teknillinen yliopisto, 2002
  5. Rönnholm, Petri: Kuvien interpolaatiomenetelmien laadun vertailua (Fotogrammetrian, kuvatulkinnan ja kaukokartoituksen erikoistyö), 2001
  6. Adobe: Piirtoalustojen, tasojen ja muiden kohteiden vieminen (Photoshopin ohje)
  7. Yunis, Alhan Anwer & Abdurrahman, Eman H.:Comparison Among Some Image Zooming Methods, University of Mosul, College of Basic Education Researchers Journal, 2013
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.