Kuvioluku

Kuvioluku on mikä tahansa luonnollinen luku, jota vastaava määrä pisteitä tai kappaleita voidaan asetella tasavälein pinnalle tai tilaan niin, että niistä syntyy jokin geometrisesti tunnistettava kuvio. Tasolle asetetut kuviot voidaan muodostaa monikulmioista, jotka ovat säännöllisiä tai muulla tavalla merkittäviä. Kun kuviolukuja muodostetaan tilaan, korvataan pisteet esimerkiksi palloilla, jotka asetellaan toisiinsa nähden rinnalle, alle tai päälle, ja saadaan kappaletta muistuttava kuvio.

Tietyn kuvioluvun muodostamiseen vaikuttaa paitsi kuvion muoto myös sen koko. Esimerkiksi kaikki kolmioluvut saadaan, kun eri määristä pisteitä muodostetaan eri kokoisia tasasivuisiksi muodostettuja kolmioita. Tiettyä kuviota vastaa yleensä ääretön lukujoukko.

Luvuilla, jotka saadaan kuvioluvuista, on mielenkiintoisia ominaisuuksia, joita tutkittiin antiikin Kreikassa ja Euroopassa 1600-luvulta asti.

Esimerkkejä

Tason kuviolukuja

Monikulmioluvut saadaan kuvioista, jotka on aseteltu säännöllisiksi kolmioiksi, neliöiksi, viisikulmioiksi tai kuusikulmioiksi. Seuraavassa näytetään, miten viisi ensimmäistä neliölukua on saatu.

Luku neljä saadaan, kun pisteen ympärille muodostetaan kolmella (punaisella) pisteellä neliö, jonka sivut muodostuvat kahdesta pisteestä. Luku yhdeksän saadaan, kun (2 x 2)-neliö laajennetaan täydentämällä sitä viidellä pisteellä (3 x 3)-neliöksi. Kuvioihin jää edelliset pisteet paikalleen, kun niitä täydennetään gnomonilla (punaiset pisteet), ja kuvioluku saadaan, kun kaikki pisteet lasketaan mukaan.

Kuusikulmioluku syntyy, kun valmiiseen kulmioon lisätään gnomon, joka täydentää kuvion taas kuusikulmioluvuksi.

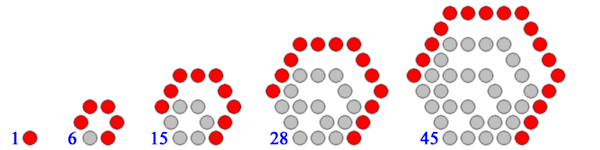
Tyhjät välit kuvion sisällä kuuluvat tämän kuviotyypin luonteeseen. Kuusikulmiolukujen gnomonit $g_{n}$ muodostavat myös lukujonon: 1, 5, 9, 13, 17, ..., joka näyttää olevan aritmeettinen lukujono $g_{n}=1+(n-1)\cdot 4$ .

Tilan kuviolukuja

Tetraderiluku 35, joka on muodostettu säännöllisen kolmion päälle

Kun tason kuvioluvut saadaan ryhmittelemällä tasolle pisteitä, tilan kuvioluvut saadaan ryhmittelemällä pieniä palloja "kasoihin" kuten kuutioiksi, pyramideiksi tai kehiksi. Tällainen ryhmittely on esimerkiksi tetraedri tai neliöpohjainen pyramidi.

Kuvassa rakennetaan neliön päälle pyramidia. Kasaa on myös nimetty tykinkuulien pinoksi.

Lähteet

Weisstein, Eric W.: Cubic Number (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)

Kuvioluvut

Monikulmioluvut	kolmioluvut neliöluvut viisikulmioluvut kuusikulmioluvut seitsenkulmioluvut kahdeksankulmioluvut yhdeksänkulmioluvut kymmenkulmioluvut yksitoistakulmioluvut kaksitoistakulmioluvut
Muita tasokuviolukuja:	keskitetyt neliöluvut keskitetyt kuusikulmioluvut tähtiluvut
Pyramidiluvut	tetraedriluvut neliöpyramidiluvut viisikulmiopyramidiluvut kuusikulmiopyramidiluvut seitsenkulmiopyramidiluvut
Muut monitahokasluvut	kuutioluvut oktaedriluvut Haűyn oktaedriluvut
Monikulmiolukuja koskevia tuloksia	Fermat’n monikulmiolause Pollockin tetraedrilukuotaksuma Pollockin oktaedrilukuotaksuma Lagrangen neljän neliön lause

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.