Kosinilause
Kosinilause on trigonometrian tulos, jonka perusteella on mahdollista määrittää kolmion kulmat, kun sen kaikki sivut tunnetaan tai kolmion tuntematon sivu, kun yksi kolmion kulma ja sen viereiset sivut tunnetaan.
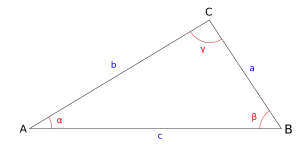
Kosinilauseessa on kolmion kulma, ja ovat kulman viereisten sivujen pituudet ja vastakkaisen sivun pituus. Kaava palautuu Pythagoraan lauseeseen, kun on suora kulma.[1]
Todistus

Oletetaan, että kulma on terävä. Olkoon h:n pituus lyhin etäisyys kolmion sivulta b sivujen a ja c yhtymään. Tällöin h voidaan esittää Pythagoraan lauseen avulla kahdella eri tavalla:
Tästä saadaan
Yhtälöstä voidaan sievennyksien jälkeen ratkaista :
Kulman kosini on kuvion mukaan
Yhtälö saadaan muotoon .
Todistus sujuu samoin, jos kulma on tylppä.
Kosinilause ja vektorit
Kosinilause on vektorikielellä olennaisesti sama asia kuin kahden vektorin erotuksen pituuden lauseke pistetulon avulla laskettuna. Ensimmäisen kuvan merkinnöin ja pistetulon perusominaisuuksia hyväksi käyttäen saadaan:
Katso myös
Lähteet
- Thompson, Jan & Martinsson, Thomas: Matematiikan käsikirja, s. 213. Helsinki: Tammi, 1994. ISBN 951-31-0471-0.