Konformaatio

Kemiassa konformaatio tarkoittaa kaikkia molekyylin kolmiulotteisia muotoja, joita muodostuu molekyylin yksöissidosten kiertyessä ja joidenkin sidosten välisten sidoskulmien muuntuessa ilman että kummassakaan tapauksessa kemiallisia sidoksia rikkoutuu. Myös trigonaalisten pyramidien inversiot (kuten amiinien) ja niiden kaltaiset muutokset voidaan lukea konformaatioiksi. Sidosten rikkoutuessa ja muodostuessa jälleen samojen atomien välille, olisi konformaatiomuutoksen sijaan kyseessä konfiguraation muuntuminen toiseksi konfiguraatioksi.[1]

Etaanin pallotikkumalli. Kaikki animaation kiertokulmat ovat konformaatioita ja niitä on ääretön määrä.

Konformaatio- ja konfiguraatiomuutosten kautta molekyylit voivat muuntua eri stereoisomeereiksi. Konformeerit ovat stereoisomeerejä. Konformeerejä ovat molekyylit, jotka konformaatiomuutoksen kautta saavuttavat paikallisen potentiaalienergiaminimin. Konformeerin energia kasvaa jos sen konformaatio muuttuu mittaamattoman pienen määrän eli infinitesimaalisesti. Tällöin molekyyli ei enää ole konformeeri.[1] Molekyylillä voi olla monia konformeerejä, eivätkä ne kaikki ole kaikkein pienienergisimpiä mahdollisista konformeereistä. Pienienergisimmän konformeerin voidaan sanoa olevan globaalissa energiaminimissä paikallisen minimin sijaan.[2]

Etaanin C-C -sidoksen kiertokulmien potentiaalienergiaerot pinkkinä käyränä, jonka huippuja kutsutaan energiavalleiksi. Energiaminimiä vastaa käyrän pohjan konformaatio A ja huipun maksimia B (esitetty Newman-projektioina). B omaa 12 kJ/mol (2.9 kcal/mol) suuremman energian kuin A.[3] A on minimissä eli se on rotameeri, jollainen taas B ei ole.[1] Etaani on valtaosan ajasta muodossa A sen energeettisen suotuisuuden takia.

Konformeria jaetaan alaluokkiin, kuten rotameereihin, joissa paikallinen energiaminimi saavutetaan vain yhden yksöissidoksen vapaalla kiertymisellä. Jos sidoskiertyminen ei ole vapaata vaikkapa steeristen esteiden takia, ovat nämä muuten samanlaiset molekyylit toistensa atropisomeerejä. Kiertyminen ei ole vapaata siihen vaadittava energia on niin suuri (IUPAC ei ole määrittänyt kuinka suuri), ettei sitä käytännössä havaita.[1]

Konformeriatyypit

Konformeriamuotoja ovat muun muassa

  • rotameria – yhden yksöissidoksen pienen energian vaatiman kiertymisen aiheuttama konformeria. Esimerkki: butaani.[1]
    • atropisomeria – kuten edellä, mutta kiertyminen vaatii esimerkiksi steeristen esteiden takia niin suuren energian, että toistensa atropisomeerit voidaan erotella toisistaan.[1] Esimerkki: BINAP.[4]
  • rengaskonformaatiot – rengasrakenteiden molekyylien kuten syklohekseenin tuoli-kierrevene -konformeria.[2]
  • laskostuminen – sanaa käytetään tavasta, jolla proteiinit ovat muodostaneet sekundääri- ja tertiäärirakenteensa.[5]
  • akamptisomeria – 2018 löydetty tyyppi.[6][7] Tämä ei kuitenkaan ole IUPAC:n tunnistama termi.

Rotameria

Rotameeri muuntuu toiseksi rotameeriksi vain yhden yksöissidoksen kiertymisen kautta. Kierros vaatii vain pienen energian.[1] Esimerkki rotameriasta on butaani (CH3-CH2-CH2-CH3), jonka edeltävän kaavan tummennettujen hiilten välisen yksöissidoksen kiertyessä muodostuu kaksi eri rotameeriä (kuva alla).

Butaanin keskisidoksen kiertokulmien potentiaalienergiaerot pinkkinä käyränä. Lomittaiset A ja B ovat paikallisissa energiaminimeissä[3] ja ovat siten rotameerejä.[1] A on kaikkein pienienergisin konformaatio, joten se on globaali energiaminimi.[2] Konformaatioiden potentiaalienergiaerot suhteessa A:han ovat 16 kJ/mol (3.9 kcal/mol), 3.8 kJ/mol (0.9 kcal/mol) ja 19 kJ/mol (4.5 kcal/mol) kuten kuvassa.[3] C ja D ovat kohdakkaisia konformaatioita.

Rotamerian analyysi
Vasen: elektroniparin omaava σ-orbitaali (HOMO) menee päällekkäin tyhjän hajottavan σ*-orbitaalin (LUMO) kanssa. Oikea: HOMO ja LUMO yhtyvät (hyperkonjugoituvat) korkea- ja pienienergiseksi orbitaaliksi. Elektronipari (kaksoisnuoli) miehittää alemman orbitaalin saaden aiempaa pienemmän energian.

Sidosten kiertymisen suotuisuutta selitetään kahdella tavalla:

  1. steerinen hyljintä – ryhmien ollessa kohdakkain, voivat niiden elektronein täytetyt molekyyliorbitaalit hylkiä toisiaan erityisesti jos ryhmät ovat suuria.[2]
  2. vahventava hyperkonjugaatio – ryhmien ollessa lomittain, voi niissä oleva elektroniparilla täytetty sitova σ-orbitaali ja elektroneista tyhjä anti-sitova σ*-orbitaali mennä päällekkäin ja yhdistyä eli hyperkonjugoitua. Muodostuu yksi alkuperäistä hajottavaa orbitaalia korkeaenergisempi hajottava orbitaali ja sitovaa pienienergisempi sitova orbitaali. Sidoselektronipari siirtyy pienienergiselle orbitaalille, madaltaen konformaation potentiaalienergiaa lisäten siten tämän muotoisen konformaation suotuisuutta.[8]

Hyperkonjugaation sijaan saatetaan myös sanoa kohdakkaisella konformaatiolla olevan kierto- eli torsionaalista jännitytystä (eng. torsional strain), erityisesti käsiteltäessä pieniä vedyn kaltaisia atomeja. Tällä viitataan ilmiöön, jossa kohdakkaisuus on epäsuotuisaa, muttei välttämättä kerrota, mistä epäsuotuisuus johtuu. Etaanilla lomittaisen konformaation suotuisuus johtuu lähinnä siitä, että energiaa madaltava hyperkonjugaatio on tässä muodossa mahdollinen. Etaanilla tämä selittää siis kohdakkaisen konformaation epäsuotuisuuden eli "torsionaalisen jännityksen" koska suotuisa hyperkonjugaatio lakkaa vaikuttamasta kohdakkaisessa muodossa.[3]

Myös butaanissa hyperkonjugaatiota voidaan pitää merkittävimpänä tekijänä. Butaanin lomittaisessa konformaatiossa, joka on merkitty tämän osion alkukuvassa A:ksi, hyperkonjugaatio madaltaa konformaation energiaa hylkivien vaikutusten ollessa vähäisiä. B:ssä hyperkonjugaatio lisää suotuisuutta, mutta metyylit ovat lähellä toisiaan aiheuttaen vähäistä steeristä hyljintää. C:ssä hyperkonjugaatio ei pääse vaikuttamaan ja lähinnä tämä lisää C:n energiaa. D:ssä hyperkonjugaatio ei vaikuta ja metyylien toisilleen aiheuttama steerinen este lisää energiaa tästä vielä hieman.[3]

Butadieeni. s-cis (vas.) ja s-trans.

Myös konjugaatio vaikuttaa. Konjugoimattomassa etaanissa kierähdys energiavallin yli vaatii 12 kcal/mol.[2] Konjugoituneen sigma- eli s-cis-butadieenin yksöissidoksen kierto s-trans-muotoon vallin yli vaatii noin 30 kJ/mol,[9] sillä konjugaatio antaa näennäiselle yksöissidokselle hieman kaksoissidosluonnetta. Dimetyyliformamidin tätä konjugoituneemman amidisidoksen 180° kierto vaatii jo 85 kJ/mol. Vertailun vuoksi 2-buteenin kierto vaatii energiaa jo noin 260 kJ/mol koska tässä on varsinainen kaksoissidos, jonka kierto vaatii piisidoksen väliaikaista rikkomista.[2] 2-buteenissa kyse ei enää kuitenkaan ole konformeriasta, koska sidoksia rikkoutuu.[1]

Atropisomeria
Orto-bifenyyleihin kuuluvan 6,6'-dinitro-2,2'-difeenihapon atropisomeerit. Nämä ovat toistensa aksiaalisia isomeerejä.

Atropisomeereissä jonkin yksöissidoksen kiertyminen on osin estynyttä, koska sidoksen täydellinen kiertyminen vaatii niin paljon energiaa ettei kiertymistä havaita käytännössä. Toistensa atropismeerit eivät spontaanisti muunnu toisikseen ja ne voidaan teoriassa erottaa toisistaan erillisinä aineina. Atropisomeerit voivat ilmentää aksiaalista kiraalisuutta. Esimerkkejä atropisomeriasta ovat jotkin substituoidut orto-bifeenylit (kuva), 1,1,2,2-tetra-tert-butyylietaani,[1] BINAP, BINOL ja telentsipiini.[4]

Rengaskonformeria

Rengaskonformeriaa ilmentävät molekyylit, joissa on rengasrakenteita. Esimerkki tästä on sykloheksaani, jossa energiaminimin muodostavat tuoliksi- ja kierreveneeksi kutsutut konformaatiot.[2] Ne ovat siten toistensa konformeerejä.[1]

Sykloheksaanin eri energiamaksimeja ja minimejä vastaavat konformaatiot: tuoli (A1/2), kierrevene (B1/2), vene (C) ja puolituoli (D1/2). A1 voi huoneenlämmössä läpikäydä helposti rengaskäännöksen muuntuen A2:ksi muiden kuvan muotojen kautta järjestyksessä A1→D1→ jne. tai päinvastoin.[2] Vene ei ole välttämätön välimuoto rengaskäännöksessä.[10] Pinkki käyrä on konformaatioiden potentiaalienergiaeroja suhteessa tuoliin. Erot ovat 43 kJ/mol (10.3 kcal/mol), 25 kJ/mol (6 kcal/mol) ja 21 kJ/mol (5 kcal/mol) kuten kuvassa. A1/2 ja B1/2 muodostavat paikalliset minimit ja ovat siksi konformeerejä.[2]

Rengasjännitys
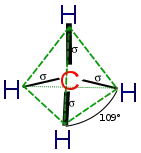
Tetaedrinen metaani. Kulmat ovat ~109.5°.

Orgaanisissa rengasrakenteissa näiden pyrkimys päästä eri konformaatioihin esimerkiksi hiilirungoltaan täysin tasomaisten rakenteiden sijaan selittyy ensisijaisesti sillä, että renkaiden hiilet pyrkivät muodostamaan ympärilleen sidokset tetraedrimuotoisesti neljään eri atomiin. Hiilissä sidosten orbitaalit ovat sp3 hybridisoituneet ihannetilanteessa noin 109.5° (tarkempi arvo noin 109.4712°) kulmiin suhteessa muihin sidoksiin. Kulmat muodostavat tetraedrin. Täysin tasomaisissa molekyyleissä kulmat eivät ole 109.5°, joten niillä on konformaation potentiaalienergiaa lisäävää rengasjännitystä. Muissa kuin tasomaisissa komformaatioissa kulmat ovat lähempänä 109.5° ihannekulmaa.[2]

Esimerkiksi tasomaisen sykloheksaanin hiilten välisten sidosten kulmat olisivat 120° (katso säännöllinen kuusikulmio) aiheuttaen rengasjännitystä. Tämä on niin suurta ettei tasomuotoa ole olemassa. Tuolisykloheksaanin sidoskulmat ovat teoriassa ihanteelliset (109.5°), eikä rengasjännitystä siten ole. Tuolin sanotaan usein olevan rengasjännityksetön. Tämä ei ole totta lähinnä siksi koska aksiaalisiin (katso Aksiaalisuus ja ekvatoriaalisuus) vetyihin vaikuttavat hylkivästi toiset saman puolen aksiaaliset vedyt. Siksi rengas pyrkii vähentämään tätä vuorovaikutusta litistymällä hieman, jolloin aksiaaliset vedyt taipuvat ekvatoriaalisemmiksi. Tuolin hiilten kulmat siksi ovat rengasjännityksen ja steerisen vaikutuksen välisenä kompromissina oikeasti noin 111.5°. Tähän hiili-hiili kulmaan vaikuttavat hieman myös hiilen sitomat vedyt. Kulmat ovat myös erilaiset hiilten ja vetyjen, sekä vetyjen ja vetyjen välillä, koska nämä eivät ole identtisiä ja vievät toisiltaan steerisesti eri verran tilaa.[10]

Renkaiden hyperkonjugaatio ja muut vaikutukset
Veneen vedyt tulevat hylkivästi lähelle toisiaan.

Hiilten väliset kulmat ovat lähes 109.5° myös venesykloheksaanissa. Siksi veneen voisi olettaa olevan energiallisesti suotuisa. Vedyt ovat kuitenkin veneessä kohdakkain, jolloin niiden σ- ja σ*-orbitaalit eivät voi kunnolla hyperkonjugoitua (katso Rotamerian analyysi). Tämä tekee veneestä epäsuotuisan. Lisäksi veneen päiden aksiaaliset vedyt tulevat lähelle toisiaan (kuva) aiheuttaen steerisen esteen, mutta tämä vaikutus on hyperkonjugaation osittaiseen puutteeseen verrattuna pieni. Kierrevenemuodossa vaikutukset ovat samankaltaiset kuin veneessä, mutta kiertynyt rakenne vähentää edeltäviä vaikutuksia; kiertymisen takia erityisesti hyperkonjugaatio pääsee vaikuttamaan potentiaalienergiaa madaltaen.[10]

Hyperkonjugaation merkitys näkyy hyvin syklopentaanissa. Sen tasomuodossa, jota ei oikeasti ole olemassa, hiilten kulmat olisivat 108° (katso säännöllinen viisikulmio) – lähes ihanteelliset. Tasossa vedyt kuitenkin ovat kohdakkain, jolloin rakennetta vakauttavaa hyperkonjugaatiota ei ole. Siksi syklopentaanin kaikkein suotuisin konformeeri on taipunut kirjekuorikonformaatio, jossa hyperkonjugaatio vaikuttaa. Kompromissina kirjekuoressa kaikki rakenteen hiilikulmat kuitenkin pienenevät ja rengasjännitys kasvaa – kirjekuoren kulmat ovat 102–106°.[10]

Renkaiden substituointi

Substituoituun hiilivetyrenkaaseen on liittynyt vetyjen tilalle substituentteja eli muita atomeita tai atomiryhmiä. Ryhmä olla vaikka hydroksyyli (katso sykloheksanoli). Monosubstituoidussa renkaassa ryhmiä on yksi, disubstituoidussa kaksi jne.

Substituenttivertailu[2]
Substi
-tuentti		 Tasapai
-nova
-kio, K		 Aksiaalisen
ja ekvatoriaali
-sen energiaero,
kJ/mol		 Ekvatoriaali
-muodon
yleisyys, %
H 1 0 50
OMe 2.7 2.5 73
Me 19 7.3 95
Et 20 7.5 95
i-Pr 42 9.3 98
t-Bu >3000 >20 >99.9
Ph 110 11.7 99

Substituoitu sykloheksaani pyrkii yleensä tuolikonformaatioon. Tästä se pyrkii rengaskäännöksen kautta tuoliksi, jossa mahdollisimman moni substituentti on ekvatoriaalisesti (katso Aksiaalisuus ja ekvatoriaalisuus). Substituentin koko vaikuttaa suotuisuuteen.[10] Esimerkiksi suuren tert-butyyliryhmän (t-Bu, taulukko) ollessa substituenttina, on se yli 3000 kertaa suuremmalla todennäköisyydellä ekvatoriaalisessa asemassa kuin aksiaalisessa. Ekvatoriaalisen konformaation energia on 20 kJ/mol pienempi kuin aksiaalisesti substituoidun. Metoksi-ryhmä (OMe) taas on pienempi, joten sen ollessa substituenttina, se on vain 2.7 kertaa todennäköisemmin ekvatoriaalisesti.[2]

Sykloheksaani voi olla disubstituoitu siten, että toinen substituentti on tuolissa aksiaalisesti ja toinen ekvatoriaalisesti. Jos nämä ovat identtisiä, ovat molemmat käännöksen tuolimuodot yhtä suotuisia. Jos toinen substituentti onkin suurempi, on se tuolimuoto suotuisampi, jossa isompi substituentti on ekvatoriaalisesti. Suotuisin konformeeri riippuu siis substituenttien koosta ja lukumäärästä edeltäviin sääntöihin pohjautuen.[10]

tert-Butyyliryhmä (tBu) on suurempi kuin hydroksyyli (OH). Siksi vasen muoto, jossa tBu on ekvatoriaalisesti, on suotuisampi.
Aksiaalinen etyylisykloheksaani. Aksiaaliset vedyt ovat steerisiä esteitä etyylille (Et).

Aksiaalisen substituoinnin epäsuotuisuus johtuu steerisestä esteestä, jonka muut aksiaaliset ryhmät aiheuttavat aksiaaliselle substituentille.[10] Konformaatioita tarkastellessa tulee kuitenkin muistaa että jotkin substituentit rajoittavat muiden substituenttien kääntymistä. Esimerkiksi karbonyyli (=O), jollainen on vaikkapa sykloheksanonissa, saa aikaan karbonyylin hiileen ja kahteen sen viereiseen hiileen tasomaisen rakenteen. Tämä johtuu karbonyylihiilen pyrkimyksestä asettua sidosorbitaaleiltaan tasokolmion muotoon sp2 hybridisaation takia.[2]

Dekaliini, jonka trans-muodon rengaskäännös vaatii sidoksen rikkoutumisen (punainen).

Sykloheksaanin lisäksi muut renkaat kuten syklobutaani ja syklopentaani voivat läpikäydä omanlaisensa rengaskäännökset. Kaikki rengasrakenteet eivät tähän pysty. Esimerkiksi kaksirenkainen cis-dekaliinin voi läpikäydä rengaskäännöksen, mutta trans-muoto ei, koska toisen renkaan käännös vaatii tämän renkaan jonkin hiilten välisen sidoksen katkeamista.[10]

Rengaskonformaatioiden nimet

Rengaskonformaatioita on useita ja näille on omat nimensä. Kruunu, josta on esimerkki alla taulukossa, on eräs muoto, jota esiintyy yli 8:n hiilen renkailla, joissa hiiliä on parillinen määrä.[1]

Alla on joitain rengaskonformaatioiden esimerkkejä. Lista ei ole täydellinen, eikä listan renkaiden kaikkia mahdollisia konformaatioita ole esitetty. Osa renkaista on konformeerejä, osa ei ole.

Rengaskonformaatioita
C lkm. Kuva Konformaation
nimi, eng. nimi		 Molekyylin
nimi
4 Taipunut, puckered Syklobutaani.
5 Kirjekuori, envelope[1] Syklopentaani.
Puolituoli, half-chair
6 Tuoli, chair[1] Sykloheksaani.
Vene, boat[1]
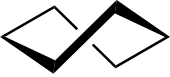Kierrevene, twist-boat
Puolituoli, half-chair[1]
7 Tuoli, chair[11] Sykloheptaani.
Vene, boat[11]
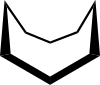
8 Kruunu, crown[12] Syklo-oktaani.
Allas, tub[1]
Vene-vene[12]
Vene-tuoli[12]
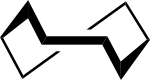
Kierre tuoli-tuoli[12]
Kierre-vene-tuoli[12]

Termistö

Kiertokulma

Yksittäisille kierto- eli dihedraalikulmille voidaan antaa nimiä ja etuliitteitä esimerkiksi rotameerien nimeämiseksi. Kulmat nimetään tiettyjen substituenttien eli atomi/atomiryhmien välisten kulmien mukaan.[1] Esimerkiksi butaanissa substituentit ovat metyylit (-CH3).

Etaani. Kohdakkainen (vasen) ja lomittainen eli gauche.

Molekyyleissä kuten etaani, joissa ryhmät ovat samoja, kutsutaan muotoja kohdakkaiseksi (eng. eclipsed) ja lomittaiseksi eli gauche-muodoksi.[1]

IUPAC:n mukaan kun kiertokulma kahden substituentin välillä on[1]

  • 0° ja ±90°, konformaatio on syn (s).
  • ±90° ja 180°, konformaatio on anti (a).
  • 30° and 150°, konformaatio on klinaali (c).
  • 0° ja ±30° tai ±150° ja 180°, konformaatio on periplanaari (p).

Edeltävät voidaan yhdistää eli kun kiertokulma on välillä[1]

  • 0° ja ±30°, konformaatio on synperiplanaari (sp) eli syn- tai cis-.
  • 30° ja 90° tai –30° ja –90°, konformaatio on synklinaali (sc) eli gauche.
  • 90° ja 150° tai –90° ja –150°, konformaatio on antiklinaali (ac).
  • ±150° ja 180°, konformaatio on antiperiplanaari (ap) eli anti- tai trans-.

Molekyyli käännetään kuvitteellisesti siten, että kiertyvä sidos kohtisuoraan poispäin katsojasta. Konformaatioille voidaan käyttää etuliitteitä ap, sp, +sc, –sc, +ac ja –ac (kirjoitetaan kursiivilla), ja makromolekyyleille vastaavasti etuliitteitä T, C, G+, G-, A+ ja A- (ei-kursiivilla). Jos takimmainen substituentti on kiertynyt katsojaa lähempänä olevasta substituentista myötäpäivään alle 150°, saa konformaatio positiivisen etuliitteen (+sc tai +ac). Jos kierto on vastapäivään alle 150°, etuliite on negatiivinen (–sc tai –ac).[1]

Aksiaalisuus ja ekvatoriaalisuus
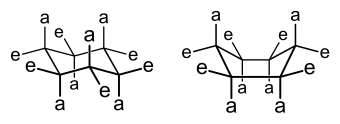
Aksiaaliset (a) ja ekvatoriaaliset (e) substituentit.

Sykloheksaanissa enemmän pystysuuntaiset substituentit ovat aksiaalisia ja enemmän renkaan rungon tasossa olevat ovat ekvatoriaalisia. Käsitettä käytetään myös muissa rengasrakenteissa kuten syklobutaanissa, syklo-oktaanissa jne. Joissain tilanteissa käytetään myös termejä pseudoaksiaalinen ja -ekvatoriaalinen.[1]

Lähteet
  1. GP Moss: Basic terminology of stereochemistry (IUPAC Recommendations 1996). Pure and Applied Chemistry, 1.1.1996, 68. vsk, nro 12, s. 2193–2222. doi:10.1351/pac199668122193. ISSN 1365-3075. Artikkelin verkkoversio.
  2. J Clayden, N Greeves, S Warren: Organic chemistry, s. 364–376, 827. 2. painos. Oxford: University Press, 2001. OCLC: 867050415. ISBN 9780199270293.
  3. J McMurry: Organic chemistry, s. 95–98, 118–120. Brooks/Cole, 2012. OCLC: 701208906. ISBN 9780840054449.
  4. AHJ Engwerda et al.: Solid Phase Deracemization of an Atropisomer. Crystal Growth & Design, 25.9.2017, 17. vsk, nro 10, s. 5583–5585. PubMed:29018306. doi:10.1021/acs.cgd.7b01180. ISSN 1528-7483. Artikkelin verkkoversio.
  5. DL Nelson & MM Cox: Lehninger principles of biochemistry, s. 140. 5. painos. New York: W.H. Freeman, 2008. OCLC: 191854286. LCCN: 2007941224. ISBN 9780716771081. Teoksen verkkoversio.
  6. PJ Canfield et al.: A new fundamental type of conformational isomerism. Nature Chemistry, 21.5.2018, 10. vsk, nro 6, s. 615–624. doi:10.1038/s41557-018-0043-6. ISSN 1755-4330. Artikkelin verkkoversio.
  7. Katrina Krämer: First new form of isomerism discovered in 50 years will be the last Chemistry World. 22.5.2018. Arkistoitu 22.5.2018. Viitattu 16.9.2018.
  8. L Song et al.: Steric Strain versus Hyperconjugative Stabilization in Ethane Congeners. The Journal of Physical Chemistry A, 2005, 109. vsk, nro 10, s. 2310–2316. doi:10.1021/jp044700s. ISSN 1089-5639. Artikkelin verkkoversio.
  9. CW Bock, P George, M Trachtman: A molecular orbital study of the rotation about the C-C bond in 1,3-butadiene. Theoretica Chimica Acta, 1984, 64. vsk, nro 4, s. 293–311. doi:10.1007/bf00551014. ISSN 0040-5744. Artikkelin verkkoversio.
  10. V Dragojlovic: Conformational analysis of cycloalkanes. ChemTexts, 12.8.2015, 1. vsk, nro 3. doi:10.1007/s40828-015-0014-0. ISSN 2199-3793. Artikkelin verkkoversio.
  11. DF Bocian, HM Pickett, TC Rounds, HL Strauss: Conformations of cycloheptane. Journal of the American Chemical Society, helmikuu 1975, 97. vsk, nro 4, s. 687–695. doi:10.1021/ja00837a001. ISSN 0002-7863. Artikkelin verkkoversio.
  12. PW Pakes, TC Rounds, HL Strauss: Conformations of cyclooctane and some related oxocanes. The Journal of Physical Chemistry, elokuu 1981, 85. vsk, nro 17, s. 2469–2475. doi:10.1021/j150617a013. ISSN 0022-3654. Artikkelin verkkoversio.

    Aiheesta muualla
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.