Keskuspaikkateoria

Kun asutuskeskusten vaikutusalueet puristuvat yhteen niiden kasvaessa, syntyy kuusikulmioverkko.

Christallerin verkko.

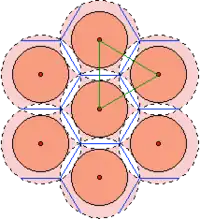
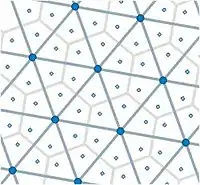
Christallerin teoria on äärimmilleen yksinkertaistettu malli, eikä tee oletuksia suurten ja pienten asutuskeskusten kokoeroista. Teoria olettaa kaikkien ihmisten osto- ja liikennekäyttäytymisen samaksi, ja alueen, jossa luonnonvarat ovat samoja. Jokaista suurta asutuskeskusta ympäröi tasavälein kuusi pienempää asutuskeskusta, eli suurta pääkeskusta ympäröi 6 pienempää alikeskusta. Keskukset ovat kolmiomaisessa liikenneyhteyksien koostamassa verkossa. Keskustan vaikutusalue on kuusikulmiomainen. Tämä on syntynyt keskusten alkuaan ympyrämäisten vaikutusalueiden puristuttua yhteen, kun keskuksia on tullut lisää[1]. Käytännössä kolmiomaista verkkoa ei yleensä esiinny, kerran synnyttyään keskukset eivät voi siirtyillä teorian vaatimille "parhaille mahdollisille" paikoille, missä etäisyydet kaikkiin naapurikeskuksiin ovat samoja. Myös suuren keskuksen hallitsemien pienten keskusten määrä vaihtelee.

Pääkeskuksessa on enemmän palveluja kuin pienemmissä keskuksissa, ja siksi ihmiset asioivat joskus suuremmissa keskuksissa. Pääkeskuksella on suuri vetovoima, joka vie tietyn osan alikeskuksesta lähtevästä liikenteestä, kaupankäynnistä jne. Kaupankäyntiä ja liikennettä tapahtuu tietenkin myös alikeskusten välillä. Tämän mukaan kaavamaisesti esimerkiksi kaupunkia ympäröi 6 kirkonkylää, ja kirkonkylää 6 pientä kylää. Malli olettaa ainakin kolmen kokoisia suuria keskuksia ja apukeskuksia.

Christallier esitti keskushierarkiastaan kolme muunnelmaa, jotka poikkeavat toisistaan siinä, kuinka monta alemman tason keskusta on olemassa kutakin ylemmän tason keskusta kohti ja miten ne sijoittuvat. Tätä ylempien ja alempien keskusten lukumäärän suhdelukua merkitään K:lla, ja sen arvo eri muunnelmissa on joko 3, 4 tai 7 (kun ylemmän tason keskus itsekin lasketaan mukaan). Sen mukaisesti erotetaan toisistaan markkina-, liikenne- ja hallintoperiaate.[2]

Markkinaperiaate

Markkinaperiaatteessa ylemmän tason keskuksen vaikutusalueen rajalla on 6 alemman tason keskusta.

Markkina- eli huoltoperiaatteessa alemman tason keskukset muodostuvat ylemmän tason keskusten muodostamien kolmioiden keskipisteeseen, jotka ovat samalla ylemmän tason keskustaa ympäröivän kuusikulmion kärkiä. Kun jokainen niistä kuuluu samanaikaisesti kolmen ylemmän tason keskuksen vaikutusalueen, lasketaan kunkin niistä kuuluvan vain yhdeksi kolmasosaksi kuhunkin vaikutusalueeseen, joten alemman tason keskuksia on kaksi kutakin ylemmän tason keskusta kohti.[3][4]Lisäksi ylemmän tason keskus kuuluu tietysti myös itsensä vaikutusalueeseen. Täten luku K saa arvon K = 6/3 + 1 = 3. Markkinaperiaatteen mukaisessa keskusjärjestelmässä on kuitenkin liikenteen järjestäminen vaikeaa.[2]

Liikenneperiaate

Liikenneperiaate K=4, pienemmät keskukset ovat suurempien puolivälissä

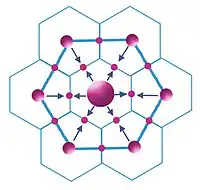
Liikenneperiaatteessa alemman tason keskukset sijaitsevat kukin kahden ylemmän tason keskuksen välissä. Ylemmän tason keskusten väliset tiet kulkevat tällöin alemman tason keskusten kautta, joista kukin on kahden ylemmän tason keskuksen vaikutuspiirissä.[5][4] Kun ylemmän tason keskusta ympäröi tässäkin kuusi alemman tason keskusta, luku K saa arvon K = 6/2 + 1 = 4.[2]

Hallintoperiaate

Hallinto K=7, suuren asutuskeskuksen ympärillä sen vaikutusalueella on kuusi alemman tason keskusta.

Sekä markkina- että liikenneperiaatteen mukaisessa keskusjärjestelmässä on vaikea muodostaa mielekkäitä eri tasoisia aluekokonaisuuksia esimerkiksi hallintoa varten. Tämä sen sijaan käy helpoiten päinsä hallintoperiaatteessa, jossa kutakin ylemmän tason keskusta ympäri kuusi alemman tason keskusta, jotka jäävät kokonaan sen vaikutusalueen sisään. Luku K saa tällöin arvon K = 6 + 1 = 7.[6]. Keskusten lukumäärä on kuitenkin paljon suurempi kuin Christallien'n järjestelmän muissa muunnelmissa, ja liikenteen järjestely on vaikeaa.[2]

Predin mallin mukaan eri alikeskusten välillä voi olla suuria vuorovaikutussuhteita, koska eri alikeskukset tuottavat erilaisia palveluita.[7]

Keskuspaikkateoriasta voidaan tehdä eräitä merkittäviä havaintoja. Ensinnäkin yritysten tuotantojen erilaiset mittakaavaedut aiheuttavat eri laajuiset markkina-alueet mikä puolestaan synnyttää kooltaan, erikoistumiseltaan ja monipuolisuudeltaan toisistaan poikkeavia kaupunkeja alueelle. Toisena jos eri toimialojen yrityksillä olisi samanlaiset mittakaavaedut suhteessa asukaskohtaiseen kysyntään, olisivat alueen kaikki kaupungit saman suuruisia keskenään. Kolmantena liikennejärjestelmän parannukset laajentavat markkina-alueita mikä vähentää yritysten määrää ja siten supistaa myös kaupunkien määrää ja kasvattaa jäljelle jääviä kaupunkeja. Kenties yllättäen paremmat liikenneyhteydet eivät siis tässä mallissa pienennä kaupunkien kokoa, vaan kasvattavat niitä.

Keskuspaikkateoria auttaa ymmärtämään eräitä kaupan alan ilmiöitä. Yksinkertaisimmillaan mallissa oletetaan yritysten myyvän homogeenisia tuotteita, jotka ovat samoja kaikissa yrityksissä. Jos kuitenkin alan tuotteet ovat vain osittain substituutteja keskenään, eli niissä esiintyy vaikka pieniäkin eroja kuluttajan kannalta, asiakkaat alkavat haluta vertailla tuotteita keskenään. Tällöin tulee useita saman alan kauppoja sijaita lähellä toisiaan, kuten tapahtuukin usein esimerkiksi huonekalu- ja autokaupassa. Silloin kun tuotteilla esiintyy komplementaarisuutta eli täydentävyyttä asiakkaiden kannattaa matkakustannusten minimoimiseksi keskittää ostoksiaan ja ostaa samalla matkalla useita tuotteita. Eri tuotteita myyvien yritysten kannattaa sijoittua lähekkäin, mikä selittää ostoskeskusten muodostumista. Molemmat mekanismit johtavat suurempiin keskittymiin eli suurempiin kokoeroihin kaupunkien välillä ja pienempään kaupunkien määrään.[8]

Teoria kuvaa hyvin maatalouden pohjalta syntyvän asutuskuvion rakenteen. Se kuvaa huonosti teollista tai jälkiteollista ympäristöä. Teoria ei ota huomioon ajallista muutosta, eikä sitä että ihmisasutukselle on ominasta väkiluvun eritahtinen kasvu. Ilmastonmuutos ja maaperän muutokset muuttavat dramaattisesti ihmisten elinoloja. Se ohittaa joitain asioita, muun muassa kaivostoiminnan synnyttämät kaupungit. Monilla alueilla asutuskeskustan jakauma riippuu luonnonvaroista. Asutus on tiheintä siellä, missä on eniten maaperän ravinteita ja muuten suotuisat olot viljan kasvatukselle.

Keskusjärjestelmä ei ajan mittaan myöskään pysy vakaana. Liikenteen kehittyessä ja ihmisten liikkuvuuden lisääntyessä yhä useammin haetaan suuremmista keskuksista sellaisetkin palvelut, jotka alemmissakin ovat tarjolla, mistä pienet keskukset joutuvat kärsimään.

Suuria asutuskeskuksia on huomattavasti vähemmän kuin pieniä. Kahden kaupungin välisen liikenteen määrä riippuu siitä, miten kaukana asutuskeskukset ovat, ja myös siitä, miten suuria asutuskeskukset ovat. Kahden suuren asutuskeskuksen välillä tapahtuu enemmän liikennettä kuin suuren ja pienen, tai vielä enemmän kuin kahden pienen. Kahden lähellä olevan keskuksen välillä liikennöidään usein, kaukana olevien harvemmin.

Niinpä liikenteen määrä kaupunkien välillä voidaan laskea kaavasta[9]

${\displaystyle T_{ab}=K*{\frac {p_{a}^{\alpha }*p_{b}^{\beta }}{d^{\delta }}}}$

Missä

• K vakio
• Tab=Liikenne kaupunkien välillä aikayksikköä kohden
• Pa,Pb= Kaupunkien a ja b väkiluvut
• α, β eksoponentit väkiluvuille, monesti 1
• d kaupunkien etäisyys
• δ kaupunkien etäisyyden eksponentti, välillä 1–2

Kaavan yksinkertaisempi muoto on

${\displaystyle T_{ab}=K*{\frac {Pa*Pb}{d}}}$

, jos eksoponentit ovat ykkösiä. Näin ollen kaupunkien välinen liikenne on kaupunkien väkiluvut kerrottuina keskenään, ja jaettuna kaupunkien välisellä etäisyydellä, ja kerrottuna kertoimella.

Tätä sanotaan gravitaatiomalliksi[10].

Vuorovaikutus keskustaan noudattaa negatiivis-eksponentiaalista jakaumaa

y=a e^-kx

jossa y vuorovaikutuksen määrä, x etäisyys, a ja b vakioita sekä e luonnollisen logaritmijärjestelmän kantaluku[11].

Vuorovaikutus voi olla liikennettä, puhelinsoittoja, sanomalehtien levikkiä, töissäkäyntiä, asiointia, muuttoja jne.

• Walter Christaller
• Walter Isard
• Tord Palander
• August Lösch
• Allan Pred
• Oiva Tuominen
• Auvo Säntti
• Mauri Palomäki
• Kauko Mikkonen

• Mikkonen, Kauko: Keskus- ja vaikutusaluetutkimus Suomessa. Teoksessa: Virkkala, Seija & Riitta Koski (toim.): Yhteiskuntamaantieteen maailma, s. 23–35. Vaasa: Vaasan yliopisto, 2009. ISBN 978-952-476-255-7 (painettu), ISBN 978-952-476-253-3 (pdf). Teoksen verkkoversio (pdf) (viitattu 9.9.2011).
• Mikkonen, Kauko: Keskus- ja vaikutusaluetutkimuksen traditio Suomessa. Terra, 2000, 112. vsk, nro 4, s. 255–260. Helsinki: Suomen maantieteellinen seura. ISSN 0040-3741.

• Kuvia tai muita tiedostoja aiheesta Keskuspaikkateoria Wikimedia Commonsissa

• Walter Christaller's Theory of Central Places (Arkistoitu – Internet Archive)
• Walter Christaller: Hierarchical Patterns of Urbanization