Kertoma

Luvun ${\displaystyle n}$ kertoma määritellään seuraavasti: [2]

${\displaystyle n!=\prod _{k=1}^{n}k=1\cdot 2\cdot 3\cdot \ldots \cdot n}$

kaikilla luonnollisilla luvuilla ${\displaystyle n\in \mathbb {N} }$.

Esimerkiksi

${\displaystyle 5!=5\cdot 4\cdot 3\cdot 2\cdot 1=120}$.

On lisäksi määritelty, että ${\displaystyle 0!=1}$, koska tyhjä tulo on ${\displaystyle 1}$. Luvun ${\displaystyle n}$ kertomaa ei ole määritelty negatiivisille luvuille tai desimaaliluvuille, ainoastaan luonnollisille luvuille.

Stirlingin approksimaatiolla voidaan arvioida kokonaisluvun kertomaa. Tämän likimääräismenetelmän tarkkuus suurenee kun käsitellään suuria kokonaislukuja. Arvioinnin menetelmää pidetään yleisesti skottilaisen matematiikon James Stirlingin kehittämänä,[3] joskin samoihin aikoihin myös ranskalainen matematiikko Abraham de Moivre oli tutkinut aihetta.[4]

Tilastollisessa termodynamiikassa tarkastellaan hiukkasjoukkoa, jonka suuruus vastaa Avogadron vakiota. Entropiaa laskettaessa tarvitaan näin suuresta hiukkasjoukosta ottaa kertoma, jonka laskeminen ilman likimääräismenetelmää on työlästä.

Stirlingin approksimaation aiheuttama suhteellinen virhe on alle 1 % jo 100:n hiukkasen järjestelmässä, joten approksimaatio on tarkka Avogadron vakion suuruiselle hiukkasjoukolle.

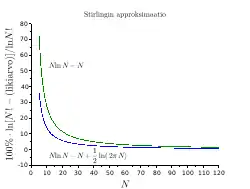
Stirlingin approksimaation johtamiseksi tarkastellaan kertoman logaritmia kun ${\displaystyle n}$ otetaan suurena lukuna:

${\displaystyle {\begin{aligned}\ln n!&\,=\,\ln {\Big [}n\cdot (n-1)\cdot (n-2)...(2)\cdot (1){\Big ]}\\&\,=\,\sum _{i=1}^{n}\ln(i)\simeq \int _{1}^{n}\ln(i)di\\&\,=\,{\Bigg |}_{i=1}^{n}n\ln n-n\,\simeq n\ln n-n\end{aligned}}}$

Euler-MacLaurin -yhtälöä käyttäen saadaan tarkempi approksimaatio:[5]

${\displaystyle \ln n!\,=\,n\ln n-n+{\frac {1}{2}}\ln(2\pi \,n)+{\frac {1}{12n}}-{\frac {1}{360n^{3}}}+{\frac {1}{1260n^{5}}}-...}$

Tästä yhtälöstä kaksi ensimmäistä termiä ovat täysin riittäviä kertoman luonnollisen logaritmin approksimaation laskemiseksi käsiteltäessä hyvin suurta hiukkasjoukkoa. Oheisessa kuvassa on esitetty havainnollisuuden vuoksi yhtälön kahden ensimmäisen termin ja toisaalta kolmen ensimmäisen termin laskentatarkkuudella suhteellisen virheen pieneneminen tarkasteltavana olevan hiukkaslukumäärän kasvaessa.

Kertoman logaritmiton Stirlingin approksimaatio on ${\displaystyle n!\simeq \left({\frac {n}{e}}\right)^{n}{\sqrt {2\pi n}}}$. Tämän lisäksi kaikilla luonnollisilla luvuilla ${\displaystyle n}$ on voimassa arvio:[6]

${\displaystyle {\sqrt {2\pi }}n^{n+{\frac {1}{2}}}e^{-n+{\frac {1}{12n+1}}}<n!<{\sqrt {2\pi }}n^{n+{\frac {1}{2}}}e^{-n+{\frac {1}{12n}}}}$

Esimerkkejä approksimaation käytöstä:

${\displaystyle \left({\frac {10}{e}}\right)^{10}{\sqrt {2\pi \cdot 10}}}$	${\displaystyle \approx }$	${\displaystyle 3\,598\,696}$
${\displaystyle \left({\frac {100}{e}}\right)^{100}{\sqrt {2\pi \cdot 100}}}$	${\displaystyle \approx }$	${\displaystyle 9{,}325\cdot 10^{157}}$
${\displaystyle \left({\frac {10^{6}}{e}}\right)^{10^{6}}{\sqrt {2\pi \cdot 10^{6}}}}$	${\displaystyle \approx }$	${\displaystyle 8{,}265\cdot 10^{5\,565\,708}}$
${\displaystyle \left({\frac {10^{9}}{e}}\right)^{10^{9}}{\sqrt {2\pi \cdot 10^{9}}}}$	${\displaystyle \approx }$	${\displaystyle 9{,}905\cdot 10^{8\,565\,705\,522}}$

Kertomilla on monia sovellutuksia lukuteoriassa. Erityisesti ${\displaystyle n!}$ on jaollinen kaikilla lukua ${\displaystyle n}$ pienemmillä ja yhtäsuurilla alkuluvuilla. Siitä seuraa, että ${\displaystyle n>5}$ on yhdistetty luku, jos

${\displaystyle (n-1)!\ \equiv \ 0\ ({\rm {mod}}\ n)}$.

Vahvempi tulos on Wilsonin lause, jonka mukaan

${\displaystyle (p-1)!\ \equiv \ -1\ ({\rm {mod}}\ p)}$,

jos ${\displaystyle p}$ on alkuluku. Ainoa kertoma, joka on myös alkuluku, on 2. On kuitenkin olemassa monia alkulukuja muotoa ${\displaystyle \scriptstyle n!\pm 1}$. Näitä alkulukuja kutsutaan kertoma-alkuluvuiksi.

Kertomafunktio voidaan ilmaista kokonaislukuargumenttisen gammafunktion ${\displaystyle \Gamma (x),(x\in \mathbb {N} )}$ avulla:

${\displaystyle n!=\Gamma (n+1)}$

.

Gammafunktion avulla kertoma voidaan määritellä myös muille kuin luonnollisille luvuille, mutta tällöin kertoman sijasta yleensä viitataan suoraan gammafunktioon.

Kertomafunktion arvo voidaan laskea kaavasta

${\displaystyle n!=\prod _{p\leq n}p^{\sum _{k=1}^{\infty }\left\lfloor {\frac {n}{p^{k}}}\right\rfloor }}$,

missä luvut ${\displaystyle p}$ ovat alkulukuja.

• Todennäköisyyslaskenta
• Gammafunktio
• Binomikerroin
• Kertomafunktio
• Primorial
• Fibonaccin kertoma

• Mathworld: Factorial (englanniksi)
• Mathworld. Stirling's Approximation (englanniksi)
• http://factorielle.free.fr (englanniksi)
• Online laskimet kertoma