Juurifunktio

Juurifunktio on muuttujan $x\!$ matemaattinen funktio, joka on potenssifunktion erikoistapaus. Se voidaan esittää yleistettynä

f\colon x\mapsto ax^{\frac {1}{n}}\qquad a\in \mathbb {R} ,n\in \mathbb {Z}

missä $x^{\frac {1}{n}}$ on potenssi ja yksikkömurtoluku ${\tfrac {1}{n}}\!$ sen eksponentti. Eksponentissa luku $n$ kutsutaan myös juuren asteeksi. Yleensä juurifunktiot rajoitetaan asteisiin n = 2, 3, 4, ..., vaikka myös aste n = 1 sopisi ominaisuuksiensa puolesta juurifunktioksi. Ylempi merkintä tarkoittaa samaa asiaa kuin Suomen koulumatematiikassa käytetty merkintä

f(x)=ax^{\frac {1}{n}}=a{\sqrt[{n}]{x}}\qquad a\in \mathbb {R}

Juurifunktion ominaisuuksia

Juurifunktion määrittelyjoukkona voi joskus olla kaikki reaaliluvut, mutta yleensä vaaditaan ei-negatiivisuutta eli $x\geq 0$ laskettavuuden parantamiseksi. Jos juuren aste $n$ on parillinen, on määrittelyjoukko rajoitettu $x\geq 0$ , mutta parittomalla asteella käyvät kaikki reaaliluvut. Tästä seuraa kuitenkin eräs yllättävä ongelma kompleksiluvuilla. Esimerkiksi negatiivisten lukujen kuutiojuuren arvon määrityksenä voisi käyttää potenssilaskennan päättelyä, jolla $(-2)^{3}=-8\Leftrightarrow {\sqrt[{3}]{-8}}=-2.$ On kuitenkin olemassa kolme kompleksilukua, joiden kolmas potenssi on $-8:$ $\{-2,1+i{\sqrt {3}},1-i{\sqrt {3}}\}$ . Jos juurilausekkeen arvoksi kelpuutetaan myös kompleksiluvut, valitaan näistä oletusarvoisesti se, jonka napakulman itseisarvo on pienin ja jos kahden kompleksiluvun napakulmien itseisarvot ovat samat, valitaan näistä positiivinen vaihtoehto. Lukujen $-2,1+i{\sqrt {3}},1-i{\sqrt {3}}$ napakulmat ovat $\pi ,{\frac {\pi }{3}},-{\frac {\pi }{3}}$ vastaavasti ja siksi lausekkeen ${\sqrt[{3}]{-8}}$ arvoksi valitaan $1+i{\sqrt {3}}$ .[1]

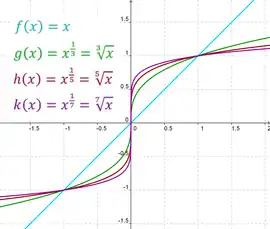Juurifunktiot, joilla on pariton aste.

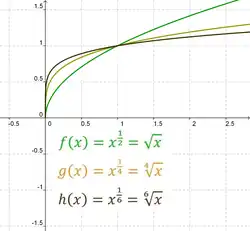Juurifunktiot, joilla on parillinen aste.

Parillisuus ja parittomuus

Juurifunktioille, joiden aste on parillinen luku, ei ole mielekästä määrittää parillisuutta ja parittomuutta, koska jo määrittelyjoukko käsittää vain positiiviset reaaliluvut. Sen sijaan parittomilla juurifunktioilla ${\sqrt {x}},$ ${\sqrt[{3}]{x}},$ ${\sqrt[{5}]{x}},\dots$ määrittelyjoukkona on kaikki reaaliluvut. Parittomat juurifunktiot ovat parittomia funktioita.

Monotonisuus

Kaikki juurifunktiot ovat aidosti monotonisia ja vieläpä aidosti kasvavia funktioita.[2]

Käänteisfunktiot

Juurifunktioiden käänteisfunktiot ovat potenssifunktioita, joiden eksponentit ovat luonnollisia lukuja $n\in \mathbb {N} :n=2,3,4,...$ . Neliöjuurifunktion $f(x)={\sqrt {x}},\ x\geq 0$ käänteisfunktio $f^{-1}(x)$ on toisen asteen potenssifunktio eli kvadraattinen funktio $f^{-1}(x)=x^{2},\ x\geq 0.$ [3] Kuutiojuurifunktion $f(x)={\sqrt[{3}]{x}},\ x\in \mathbb {R}$ käänteisfunktio on $f^{-1}(x)=x^{3},\ x\in \mathbb {R} .$

Yleistäen voidaan todeta, että käänteisfunktiot ovat parillisilla asteilla $2n$

f(x)={\sqrt[{2n}]{x}},\ x\geq 0\rightarrow f^{-1}(x)=x^{2n},\ x\geq 0

ja parittomilla asteilla $2n+1$

f(x)={\sqrt[{2n+1}]{x}},\ x\in \mathbb {R} \rightarrow f^{-1}(x)=x^{2n+1},\ x\in \mathbb {R} .

Derivointi ja integrointi

Yleinen potenssien derivaatta, kun $r\in \mathbb {R}$ lasketaan

Dx^{r}=rx^{r-1}.

[4]

Kun juurifunktion aste on $n$ , tulee derivaataksi

D{\sqrt[{n}]{x}}=Dx^{\tfrac {1}{n}}={\frac {1}{n}}x^{{\tfrac {1}{n}}-1}={\frac {1}{n}}x^{-{\tfrac {n-1}{n}}}={\frac {1}{n}}{\frac {1}{{\sqrt[{n}]{x}}^{n-1}}}

[4]

tai vaihtoehtoisesti

D{\sqrt[{n}]{x}}={\frac {1}{n}}x^{-{\tfrac {n-1}{n}}}={\frac {1}{n}}{\frac {1}{x^{\tfrac {n-1}{n}}}}={\frac {1}{n}}{\frac {1}{x^{1-{\tfrac {1}{n}}}}}={\frac {1}{n}}{\frac {\sqrt[{n}]{x}}{x}}.

[4]

Neliöjuuren derivaatta on siten

D{\sqrt {x}}={\frac {1}{2{\sqrt {x}}}}

[3]

ja kuutiojuuren derivaatta

D{\sqrt[{3}]{x}}={\frac {1}{3{\sqrt[{3}]{x}}^{2}}}={\frac {\sqrt[{3}]{x}}{3x}}

[4]

ja neljäsjuuren derivaatta

D{\sqrt[{4}]{x}}={\frac {1}{4{\sqrt[{4}]{x}}^{3}}}={\frac {\sqrt[{4}]{x}}{4x}}.

[4]

n-asteisen juurifunktion yleinen integraalifunktio saadaan

\int x^{r}dx={\frac {1}{r+1}}x^{r+1}+C\!

[4]

eli

\int x^{\tfrac {1}{n}}\ dx={\frac {1}{1+{\tfrac {1}{n}}}}x^{1+{\tfrac {1}{n}}}+C\!={\frac {n}{n+1}}x^{\tfrac {n+1}{n}}+C\!={\frac {n}{n+1}}x{\sqrt[{n}]{x}}+C

[4]

Silloin neliöjuuren integraali on

\int {\sqrt {x}}\ dx={\frac {2}{3}}x^{\tfrac {3}{2}}+C={\frac {2}{3}}x{\sqrt {x}}+C.

[4]

ja kuutiojuuren integraali

\int {\sqrt[{3}]{x}}\ dx={\frac {3}{4}}x^{\tfrac {4}{3}}+C={\frac {3}{4}}x{\sqrt[{3}]{x}}+C

[4]

Kompleksiluvut

Juurifunktioiden määrittelyjoukko voidaan laajentaa koskemaan kompleksilukuja $z\in \mathbb {C}$ . De Moivre'n teoreemassa, jossa kompleksiluvun $z$ reaalilukuinen potenssi $p$ esitetään polaarisessa muodossa

z^{p}=[r(\cos \theta +i\sin \theta )]^{p}=r^{p}(\cos p\theta +i\sin p\theta ),

[5]

voidaan vaihtaa potenssi yksikkömurtoluvuksi $p={\tfrac {1}{n}}$

z^{\tfrac {1}{n}}=[r(\cos \theta +i\sin \theta )]^{\tfrac {1}{n}}=r^{\tfrac {1}{n}}(\cos {\tfrac {\theta +2k\pi }{n}}+i\sin {\tfrac {\theta +2k\pi }{n}}),

kun $k=0,1,2,...,n-1.$ [5]

Neliöjuuri

Neliöjuurelle ${\sqrt {z}}$ saadaan kaksi arvoa, kun $k=0$ ja $1.$

Ensimmäinen juuri on arvoltaan $r^{\tfrac {1}{2}}(\cos {\tfrac {\theta +2\cdot 0\cdot \pi }{2}}+i\sin {\tfrac {\theta +2\cdot 0\cdot \pi }{2}})={\sqrt {r}}(\cos {\tfrac {\theta }{2}}+i\sin {\tfrac {\theta }{2}})$

ja toinen $r^{\tfrac {1}{2}}(\cos {\tfrac {\theta +2\cdot 1\cdot \pi }{2}}+i\sin {\tfrac {\theta +2\cdot 1\cdot \pi }{2}})={\sqrt {r}}(\cos {\tfrac {\theta +2\pi }{2}}+i\sin {\tfrac {\theta +2\pi }{2}})$

eli ${\sqrt {z}}=\{{\sqrt {r}}(\cos {\tfrac {\theta }{2}}+i\sin {\tfrac {\theta }{2}}),{\sqrt {r}}(\cos {\tfrac {\theta +2\pi }{2}}+i\sin {\tfrac {\theta +2\pi }{2}})\}$

Esimerkki neliöjuurella

Jos lasketaan kompleksiluvun $z=1+i{\sqrt {3}}$ neliöjuuri, muutetaan se ensin polaarimuotoon. Modulus on $r={\sqrt {1^{2}+{\sqrt {3}}^{2}}}=2$ ja napakulma $\tan \theta ={\tfrac {\sqrt {3}}{1}}={\sqrt {3}}$ eli $\theta =60^{\circ }.$ Siten $z=1+i{\sqrt {3}}=2(\cos 60^{\circ }+i\sin 60^{\circ })=2({\tfrac {1}{2}}+i{\tfrac {\sqrt {3}}{2}}).$ Neliöjuureksi saadaan sitten kaksi arvoa

{\sqrt {z}}={\sqrt {1+i{\sqrt {3}}}}=\{{\sqrt {2}}(\cos {\tfrac {60^{\circ }}{2}}+i\sin {\tfrac {60^{\circ }}{2}}),{\sqrt {2}}(\cos {\tfrac {60^{\circ }+360^{\circ }}{2}}+i\sin {\tfrac {60^{\circ }+360^{\circ }}{2}})\}

=\{{\sqrt {2}}(\cos 30^{\circ }+i\sin 30^{\circ }),{\sqrt {2}}(\cos 210^{\circ }+i\sin 210^{\circ })\}=\{{\sqrt {2}}({\tfrac {1}{2}}+{\tfrac {\sqrt {3}}{2}}i),{\sqrt {2}}(-{\tfrac {\sqrt {3}}{2}}-{\tfrac {1}{2}}i)\}=\{{\tfrac {1}{\sqrt {2}}}+{\tfrac {\sqrt {3}}{\sqrt {2}}}i,-{\tfrac {\sqrt {3}}{\sqrt {2}}}-{\tfrac {1}{\sqrt {2}}}i\}

Kuutiojuuri

Kuutiojuuri antaa kolme arvoa, kun $k=0,1,2.$

{\sqrt[{3}]{z}}=\{{\sqrt[{3}]{r}}(\cos {\tfrac {\theta }{3}}+i\sin {\tfrac {\theta }{3}}),{\sqrt[{3}]{r}}(\cos {\tfrac {\theta +2\pi }{3}}+i\sin {\tfrac {\theta +2\pi }{3}}),{\sqrt[{3}]{r}}(\cos {\tfrac {\theta +4\pi }{3}}+i\sin {\tfrac {\theta +4\pi }{3}})\}

Neljäsjuuri

Neljäs antaa neljä arvoa, kun $k=0,1,2,3.$ ${\sqrt[{4}]{z}}=\{{\sqrt[{4}]{r}}(\cos {\tfrac {\theta }{4}}+i\sin {\tfrac {\theta }{4}}),{\sqrt[{4}]{r}}(\cos {\tfrac {\theta +2\pi }{4}}+i\sin {\tfrac {\theta +2\pi }{4}}),{\sqrt[{4}]{r}}(\cos {\tfrac {\theta +4\pi }{4}}+i\sin {\tfrac {\theta +4\pi }{4}}),{\sqrt[{4}]{r}}(\cos {\tfrac {\theta +6\pi }{4}}+i\sin {\tfrac {\theta +6\pi }{4}})\}$

Katso myös

Lähteet

Weisstein, Eric W.: Cube Root (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)

Viitteet

Kivelä, Simo K.: Lukiotason matematiikan tietosanakirja (html) (Juurifunktion määritelmän laajennus) 2001. Helsinki: Teknillinen korkeakoulu.
Jyväskylän Yliopisto: Juurifunktio
Weisstein, Eric W.: Square Root (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
Weisstein, Eric W.: Power (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
Spiegel, Murray R.: Mathematical Handbook of Formulas and Tables. New York: McGraw-Hill Book Company, 1968. (englanniksi)

Kirjallisuutta

Rikkonen, Harri: Matematiikan pitkä peruskurssi II: Reaalimuuttujan funktioiden differentiaalilasku. Helsinki: Otakustantamo, 1969. ISBN 951-671-022-0.
Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf). Viitattu 8.7.2019.

Aiheesta muualla

Etälukio: Juurifunktio (Arkistoitu – Internet Archive)
Jyväskylän Yliopisto: Potenssi- ja juurifunktiot sekä rationaalipotenssit

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[jyv2-1] Kivelä, Simo K.: Lukiotason matematiikan tietosanakirja (html) (Juurifunktion määritelmän laajennus) 2001. Helsinki: Teknillinen korkeakoulu.

[jyv1-2] Jyväskylän Yliopisto: Juurifunktio

[sqrt-3] Weisstein, Eric W.: Square Root (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)

[power-4] Weisstein, Eric W.: Power (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)

[hb-5] Spiegel, Murray R.: Mathematical Handbook of Formulas and Tables. New York: McGraw-Hill Book Company, 1968. (englanniksi)