Inversio ympyrän suhteen

Jos piste P sijaitsee ympyrän sisällä, piirretään puolisuoralle MP normaali pisteeseen P. Normaali leikkaa ympyrän kahdessa pisteessä Q ja Q'. Koska Q on kehäpiste, voidaan siihen piirtää ympyrän säteet MQ ja MQ'. Säteen normaali on ympyrän kehällä sen tangentti. Tangentit leikkaavat toisensa janan MP jatkella, missä sijaitsee inversiopiste P'. Se, että kyseessä on juuri inversiopiste, nähdään yhdenmuotoisista kolmioista [1][4]

${\displaystyle \Delta OPQ\sim \Delta OQP'}$

seuraa

${\displaystyle {\frac {OP}{OQ}}={\frac {OQ}{OP'}}\Leftrightarrow OP\cdot OP'=OQ^{2}\Leftrightarrow OP\cdot OP'=r^{2}.}$

Inversiopisteen P' määrittäminen geometrisesti, kun piste P on inversioympyrän (punainen) ulkopuolella.

Jos piste sijaitsee inversioympyrän ulkopuolella, suoritetaan kuvion piirtäminen käänteisessä järjestyksessä. Aloitetaan etsimällä tangenttipiste ympyrältä. Sitä varten piirretään apuympyrä, jonka halkaisija on inversioympyrän keskipiste ja piste P. Thaleen lauseen nojalla apuympyrän kehällä olevan pisteen halkaisijaa vastaan oleva kehäkulma on suora. Halkaisijan toinen pää alkoi inversioympyrän keskipisteestä, josta piirretty jana on sen säde kun se päättyy inversioympyrän kehälle. Näin tapahtuukin ympyröiden leikkauspisteessä N. Siinä pisteessä kehäkulman toinen kylki on säde ja toinen jana, joka päättyy pisteeseen P. Thaleen lauseen mukaan säteen ja janan välinen kulma on suora ja jana on siten inversioympyrän tangentti. Samalla tavalla voidaan muodostaa inversioympyrän toiselle puolelle toinen tangentti pisteeseen N'. Piirretään pisteiden N ja N' välille suora. Se leikkaa pisteen P ja keskipisteen O yhdistävällä suoralla olevassa pisteessä P'.[1][4]

Kukin piste P kuvautuu inversioympyrän toiselle puolelle pisteeksi P' linjaan inversiokeskuksen O ja pisteen P kautta kulkevalle puolisuoralle. Pisteen P' etäisyys inversiokeskuksesta O on säteen neliön ja välimatkan OP osamäärä

${\displaystyle OP'={\tfrac {r^{2}}{OP}}.}$

Jos piste P osuu inversioympyrän kehälle, kuvautuu se itseensä. Jos piste P osuu inversiokeskukseen O, kuvautuu se "äärettömän kauaksi" ja sellainen kuvaus on jätetty määritelmästä ongelmallisena pois.[5][6]

Piirretään kolme pistettä A, B ja C. Nämä kuvautuvat pisteiksi A', B' ja C'. Kulmat ovat ${\displaystyle \measuredangle }$ABC = ${\displaystyle \measuredangle }$A'B'C' yhtäsuuret kaikissa tapauksissa, jossa mikään piste ei sijaitse inversiokeskuksessa O. Voidaan sanoa, että inversiokuvaus säilyttää kuvion kulman suuruuden. Inversion peilaavasta luonteesta seuraa kuitenkin käänteisyys. Jos kulma aukeaa inversioympyrää kohti, tekee kuvauksen kulma samoin, ja päinvastoin.[5][6]

Pisteen P inversio kuvautuu pisteeksi P', joka sijaitsee janan OP jatkeella.

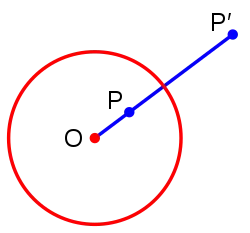
Piirretään suora, joka kulkee inversiokeskuksen O kautta. Määritelmän johdosta kaikki pisteet P kuvautuvat O:n ja P:n kautta kulkevalle puolisuoralle. Silloin O:n kautta piirretyn suoran kuvapisteet kuvautuvat kukin takaisin omalle suoralle samalle puolelle pistettä O, missä itse P on.[7][8]

Piirretään suora kulkemaan inversioympyrän ohi ja suoritetaan sen pisteille inversiokuvaus. Kuvauksen kuvapisteet asettuvat ympyrälle, joka kulkee inversiokeskuksen O kautta. Suoran kulkiessa koko ajan inversioympyrän ulkopuolella, sijaitsee kuvausympyrä inversioympyrän sisällä. Jos suora leikkaa inversioympyrää, sijaitsee kuvaympyrä osittain inversioympyrän ulkopuolella. Sekä suora että kuvausympyrä leikkaavat toisensa inversioympyrän kanssa kahdessa yhteisessä pisteessä. Inversiokuvaus on täysin käänteinen. Ympyrä, joka kulkee inversiokeskuksen kautta, kuvautuu kuvasuoraksi edellä esitetyllä tavalla.[7][9]

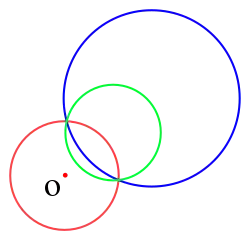
Piirretään ympyrä, jonka kehä ei kulje inversiokeskuksen kautta (vertaa edelliseen tapaukseen). Kuvauksen pisteet asettuvat kuvaympyrälle, joka on eri ympyrä kuin piirretty ympyrä. Jos ympyrä piirretään inversioympyrän ulkopuolelle, kuvautuu kuvaympyrä inversioympyrän sisäpuolelle. Kun ympyrä piirretään inversioympyrän sisäpuolelle, piirtyy kuvaympyrä inversioympyrän ulkopuolelle. Jos ympyrä piirretään leikkaamaan inversioympyää, kulkee myös kuvaympyrä piirretyn ympyrän ja inversioympyän leikkauspisteiden kautta. Inversiokuvaus on tässäkin täysin käänteinen. Kuvaympyrä kuvautuu takaisin piirretyksi ympyräksi.[10][11]

Ortogonaalisten ympyröiden kehät leikkaavat toisensa kohtisuorasti, mikä nähdään ympyröiden säteistä, jotka ovat leikkauspisteissä kohtisuorassa toisiinsa nähden. Kun piirretään ympyrä, joka on ortogonaalinen inversioympyrän kanssa, kuvautuu se kuvaympyräksi. Kuvaympyrä on identtinen piirretyn ympyrän kanssa. Sanotaan, että piirretty ympyrä kuvautuu itseensä.[5][12]