Histogrammi
Histogrammi on tilastotieteessä yleisesti käytetty graafinen esitys eli diagrammi tilastollisesta luokitellusta aineistossa. Se on pylväskaavio, joka koostuu suorakulmion muotoisista pinnoista eli pylväistä. Histogrammissa pylvään pinta-ala on verrannollinen luokan prosentuaaliseen osuuteen.[1]


Kuvaajan piirtäminen
Pylväät piirretään vaaka-akselille, jonka asteikko seuraa aineiston lukuarvoja. Kunkin pylvään vasen ja oikea reuna piirretään asteikolle luokan alku- ja loppuarvojen kohdalle. Pylvään leveys kuvaa siten luokkaväliä. Pylvään korkeus määräytyy luokan sisältämien arvojen lukumäärän eli frekvenssin mukaan, kun luokitus on tasavälinen. Pylvään pinta-ala on aina verrannollinen frekvenssin suuruuteen. Kun luokitus on muu kuin tasavälinen, pylvään korkeus kuvaa luokan suhteellista frekvenssiä suhteutettuna luokkavälin pituuteen. Tällöin pystyakselilla on luokkien frekvenssitiheydet.[1]
Histogrammi piirretään käsin laskemalla ensin kunkin luokan prosentuaalinen osuus. Sitten piirretään vaaka-akseli niin, että aineiston pienin ja suurin luokkaraja mahtuu vaaka-akselille. Pystyakselin korkeus piirretään halutun korkuiseksi niin, että syntyy tavoiteltu graafinen vaikutelma. Pystyakselin prosentuaalinen asteikko valitaan sellaiseksi, että korkein pylväs ulottuu diagrammin yläreunaan. Pylväiden korkeudet ovat prosenttuaalisen osuuden korkuisia. Pystyasteikoksi voidaan valita myös frekvenssit.[1]
Joskus pylväiden leveys asetetaan yhtä suureksi, jolloin suorakaiteen korkeus on suoraan verrannollinen luokan frekvensseihin.[1]
Värihistogrammi
Histogrammi voidaan luoda digitaalisesta kuvasta. Digitaalikameroissa ja kuvankäsittelyohjelmissa histogrammi muodostetaan kuvan pikseleistä, ja sen avulla voidaan säätää valotusta. Kuvan histogrammi muodostetaan pikseleiden kirkkausarvojen jakautumasta tai väreistä (esimerkiksi RGB-malli) kanavakohtaisesti.
Yhteys todennäköisyyslaskentaan
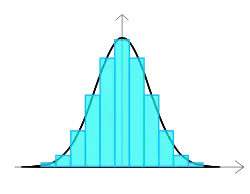
Kun aineisto kasvaa suureksi ja luokkavälejä pienennetään, piirtyy histogrammi loivapiirteisenä. Histogrammin reunaviivaa voidaan approksimoida sileällä käyrällä, joka aineiston kasvaessa ja luokkavälien pienentyessä lähestyy ideaalista tiheysfunktion käyrää. Tiheysfunktio kuvaa jatkuvan satunnaismuuttujan arvojen todennäköisyyden jakautumista vaaka-akselilla.[2]
Lähteet
- Alatupa, Sami et al.: Pitkä Sigma 6, s. 6−41. (lukion pitkän matematiikan oppikirja). Helsinki: Otava, 2010. ISBN 978-951-31-5343-4.
- Alatupa, Sami et al.: Pitkä Sigma 6, s. 153−180. (lukion pitkän matematiikan oppikirja). Helsinki: Otava, 2010. ISBN 978-951-31-5343-4.