Funktion epäoleellinen raja-arvo
Funktion epäoleellinen raja-arvo on matematiikassa analyysin ja differentiaali- ja integraalilaskennan peruskäsitteitä. Erotukseksi funktion raja-arvon yläkäsitteestä, funktion epäoleellisella raja-arvoilla tarkoitetaan jatkuvien funktioiden raja-arvolaskentaa, missä tutkitaan funktion käyttäytymistä kaukana origosta. Usein sanotaan, että "tutkitaan funktion käyttäytymistä äärettömässä tai miinus äärettömässä". Jos epäoleellinen raja-arvo on olemassa, sanotaan että funktio suppenee (muutoin hajaantuu).[1]
Johdanto
Rationaalilausekkeen epäoleelliset raja-arvot

Yksinkertaisin rationaalifunktio on
joka määritelty kaikilla reaalilukuarvoilla paitsi nollassa (ykköstä ei voi jakaa nollalla). Koordinaatistossa näkyy vain osa funktion kuvaajasta, koska sen käyrä katoaa kuviosta sen ylä- ja alapuolelle sekä molemmille sivuille. Epäoleellisella raja-arvolla voidaan selvittää, minne käyrä muualla piirtyy. Tähän tarvitaan neljä epäolellista raja-arvoa.[2]
Origon oikealla puolella funktio saa positiivisia arvoja. Kuvaajan käyrän mukaan funktio on vähenevä, koska kun muuttujan arvot kasvavat, eli kun liikutaan x-akselilla oikealle, pienenevät funktion arvot. Ne eivät kuitenkaan muutu negatiivisiksi, vaan pysyvät positiivisina lähestyen nollaa. Nolla-arvoa ei kuitenkaan saavuteta tietyssä pisteessä, mutta valitsemalla yhä suurempia ja suurempia muuttujan x arvoja päästään niin lähelle nollaa kuin vain halutaan. Tässä mielessä voidaan sanoa, että kun muuttujaa x kasvatetaan yli kaikkien rajojen, suppenee funktion arvot raja-arvoksi nolla. Tämä on eräs tapa kuvailla epäolellinen raja-arvo. Silloin voidaan sanoa, että äärettömässä funktio suppenee tai tulee nollaksi. Vastaavalla tavalla voidaan todeta, että myös vasemmalla puolella lukusuoraa voidaan käydä samanlainen prosessi. Silloin funktion negatiiviset arvot lähestyvät epäoleellisesti nollaa, kun muuttuja x pienenee alle kaikkien rajojen. Silloin voidaan sanoa, että miinus äärettömässä funktiosta tulee nolla.[2]
Epäoleellisiksi tarkasteluksi voidaan joskus katsoa myös raja-arvoa määrittelyalueen puuttuvassa pisteessä. Edellisen funktiota ei voi laskea nollassa, koska se aiheuttaisi nollalla jakamisen. Kun raja-arvoa lasketaan lähestymällä nollaa oikealta eli positiivisilla arvoilla, kasvaa funktion arvot yli kaikkien rajojen eli raja-arvo hajaantuu plus äärettömäksi. Vastaavasti, kun nollaa lähestytään negatiiviselta puolelta, hajaantuu raja-arvo miinus äärettömäksi.[3]
Yksinkertainen polynomi on potenssifunktio
joka on määritelty kaikilla reaalilukuarvoilla, ja sen kuvaajasta näkyy koordinaatistossa vain osa. Osoittautuu, että mitä suuremmilla muuttujan x arvoilla funktion arvoja lasketaan, sitä suuremmaksi funktion arvot kasvavat. Samoin, mitä pienemmillä muuttujan arvoilla funktion arvoja lasketaan, sitä pienemmiksi ne tulevat. Kummassakin tapauksessa funktion arvot hajaantuvat. Ensin mainitussa tilanteessa sanotaan myös, että funktion arvo on ääretön, kun muuttuja x on ääretön taikka äärettömässä funktio tulee äärettömäksi. Toisessa tilanteessa funktio on miinus ääretön, kun x on miinus ääretön taikka miinus äärettömässä funktiosta tulee miinus ääretön.[2]
Suppeneminen ja hajaantuminen
Funktion epäoleellisella raja-arvolla tarkoitetaan funktion arvojen tutkimista, kun muuttujan arvo joko kasvaa tai vähenee rajatta. Tällöin sanotaan, että muuttuja on plus ääretön tai miinus ääretön. Kyseessä ei ole enää funktion käyttäytymisestä yhden pisteen lähiympäristössä, vaan sitä käytetään tutkittaessa funktion käyttäytymistä origosta katsottuna "kaukaisilla" arvoilla ja hyvin pitkillä väleillä. Tarkastelutapa poikkeaa siten tavallisesta funktion raja-arvosta.
Kun muuttujan arvo kasvaa rajatta ja funktion arvot suppenevat, se merkitään
Funktion lauseke lasketaan tällöin yhä suuremmilla ja suuremmilla arvoilla (voidaan sanoa "kun x lähestyy plus ääretöntä"). Kun muuttuja vähenee rajatta ja funktion arvot suppenevat, se merkitään
Funktion lauseke lasketaan yhä pienemmillä (negatiivisilla) arvoilla (voidaan sanoa "kun x lähestyy miinus ääretöntä"). Tällöin sanotaan, että "funktiolla on positiivisessa / negatiivisessa äärettömyydessä raja-arvo L".
Kun funktion arvot lähestyvät edellä kerrotulla tavalla lukua L, voidaan kuvaajaan piirtää vaakasuora . Tätä suoraa kutsutaan funktion kuvaajan asymptootiksi.
Jos funktion arvot hajaantuvat eikä raja-arvoa ole olemassa, se merkitään esimerkiksi
jos tulos kasvaa rajatta ja
jos tulos vähenee rajatta.[2][4][5]
Funktion arvot hajaantuvat, jos funktion arvot eivät ole rajoitettuja. Jos vähenevä funktio ei ole rajoitettu alhaalta, tulee funktion epäoleelliseksi raja-arvoksi miinus ääretön. Ellei kasvava funktio ole rajoitettu ylhäältä, tulee funktion raja-arvoksi ääretön.[6]
Hajaantuvan funktion kulkua voi "ohjata" vino asymptoottisuora tai -käyrä. Asymptootin selvittäminen mallintaa funktion kuvaajan kulkua selvemmin.
Määritelmä
Funktion epäoleellinen raja-arvo, josta tässä otetaan esimerkkinä
määritellään eksaktisti epsilon-M-tekniikalla
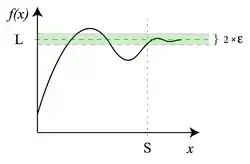
eli funktion arvo on :n etäisyydellä raja-arvosta L, kun muuttuja x on ylittänyt rajan . Intuitiivisesta voidaan ajatella, että funktion arvot osuvat riittävän lähelle raja-arvoa L, kunhan muuttuja x kasvatetaan tarpeeksi suureksi.[1][6]
Esimerkki suppenemisesta ja hajaantumisesta
Funktion epäoleellinen suppeneminen kohti arvoa nolla voidaan osoittaa seuraavasti. Kun , on aina . Valittiinpa luku kuinka pieneksi tahansa, löytyy lopulta aina sellainen muuttujan x raja , että
missä . Näin ollen funktio suppenee nollaksi, kun x kasvaa rajatta.[6]
Funktion epäoleellinen hajaantuminen äärettömyydessä voidaan osoittaa seuraavasti. Kun , on aina , joten valittiinpa luku miten suureksi tahansa, on heti, kun . Siten funktio hajaantuu äärettömäksi, kun muuttuja x kasvaa yli kaikkien rajojen.[6]
Esimerkkejä alkeisfunktioista
| Alkeisfunktio | Esimerkkejä | ||
|---|---|---|---|
| potenssifunktio , missä n on pariton | |||
| potenssifunktio , missä n on parillinen | |||
| juurifunktio , missä n on pariton | |||
| juurifunktio , missä n on parillinen | |||
| eksponenttifunktio , missä | |||
| eksponenttifunktio , missä | |||
| eksponenttifunktio , missä | |||
| logaritmifunktio , missä |
Epäoleelliseen raja-arvoon liittyviä sääntöjä
Esimerkki
Esimerkiksi polynomin käyttäytyminen äärettömyyksissä voidaan päätellä yksittäisten potenssien käyttäytymisestä. Kun lasketaan
ja huomioidaan, että , , ja , saadaan
Polynomi hajaantuu siten kohti .
Äärettömän laskusääntöjä epäoleellisessa raja-arvossa
Seuraavat merkinnät tarkoittavat raja-arvojen tuloksia. Jos funktion arvot hajaantuvat kohti plus ääretöntä, merkitään sen tulosta , jos ne hajaantuvat kohti miinus ääretöntä, niin se merkitään . Mikäli funktio suppenee kohti reaalilukua, merkitään se positiivisena ja negatiivisena . Tilanteissa, jossa raja-arvon merkillä ei ole väliä, se merkitään . Aluksi on lueteltu tapauksia, jossa lopputulos voidaan päätellä.[7]
| Yhteen- ja vähennyslaskut | Kertolaskut | Jakolaskut | Potenssit |
|---|---|---|---|
| , kun | |||
| , kun | |||
| , kun | |||
| , kun | |||
Seuraavien laskutoimitusten tulosta ei pystytä suoralta kädeltä määrittämään:[5][7]
Katso myös
- Funktion asymptootit
- Epäoleellinen integraali
Lähteet
- Stover, Christopher.: Limit (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- Alatupa, Sami & Hassinen, Sanna & Hemmo, Katariina & Leikas, Mika: Pitkä Sigma 7, s. 180–187. (lukion pitkän matematiikan oppikirja). Helsinki: Sanoma Pro, 2014. ISBN 978-952-63-0307-9.
- Kontkanen, Pekka & Lehtonen, Jukka & Luosto, Kerkko: Pyramidi 13 – Differentiaali- ja integraalilaskennan jatkokurssi, s. 42–46. (lukion pitkän matematiikan oppikirja). Helsinki: Tammi. ISBN 978-951-26-5407-9.
- Weisstein, Eric W.: Infinity (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- Weisstein, Eric W.: Indeterminate (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- Hurri-Syrjänen, Ritva: Differentiaali- ja integraalilaskenta I, (luentomoniste, s. 36–38), Helsingin yliopisto, 1999
- Kontkanen, Pekka & Lehtonen, Jukka & Luosto, Kerkko: Pyramidi 13 – Differentiaali- ja integraalilaskennan jatkokurssi, s. 31–32. (lukion pitkän matematiikan oppikirja). Helsinki: Tammi. ISBN 978-951-26-5407-9.
Aiheesta muualla
- Jyväskylän yliopisto: Epäoleellinen raja-arvo, katsottu 4.10.2014
- Internetix: Raja-arvo käsitteen laajennus, Epäoleelliset raja-arvot, katsottu 4.10.2014
