Ekvipotentiaali

Ekvipotentiaali eli isopotentiaali on matematiikassa ja fysiikassa avaruuden alue, jonka jokaisessa pisteessä jonkin vektori­kentän potentiaalilla on sama arvo.[1][2] Tavallisimmin kyseessä on tällöin skalaaripotentiaali, mutta käsitettä voidaan soveltaa myös vektoripotentiaaleihin.[3] Vektori­kentän skalaari­potentiaali on reaali­arvoinen funktio, jonka gradientin arvot avaruuden eri pisteissä muodostavat kyseisen vektori­kentän. Yleensä n-ulotteisessa avaruudessa skalaari­potentiaali­funktion ekvi­potentiaali on n-1 -ulotteinen. Jos kenttä kuitenkin on jollakin avaruuden n-ulotteisella alueella nolla, käsittää ekvi­potentiaali koko tämän alueen.

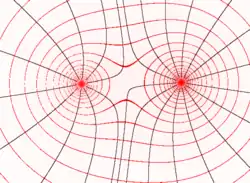
Ekvipotentiaaleja kahta vastakkaismerkkistä varausta ympäröivässä sähkökentässä.
Ekvipotentiaalikäyrät (punaiset) ja kenttäviivat (mustat) kahden samanmerkkisen pistemäisen varauksen ympärillä

Ekvipotentiaalipinta

Kolmi­ulotteisessa avaruudessa määritellyn skalaari­potentiaalin ekvi­potentiaalit ovat normaalisti pintoja, ja niitä sanotaan usein ekvipotentiaali­pinnoiksi[4] nivoo­pinnoiksi[5][6] vaki­­opotentiaali­pinnoiksi.[7] tai suomeksi myös tasa-arvopinnoiksi.[8] Ekvipotentiaali saattaa kuitenkin olla myös kolmi­ulotteinen avaruuden alue, mikäli kentän arvo kyseisellä alueella on kaikkialla nolla.

Kun ekvipotentiaali on pinta, skalaari­potentiaalin gradientti on kaikkialla kohti­suorassa tätä pintaa vastaan. [4][8] Kentän kenttäviivat ovat gradientin suuntaisia ja näin ollen ne leikkaavat ekvi­potentiaali­pinnat kaikkialla kohti­suorasti.[8] Jos taas ekvi­potentiaali käsittää kokonaisen avaruuden alueen, on skalaari­potentiaali tällä alueella vakio, ja sen gradientti on koko alueella nolla.

Fysikaalisia esimerkkejä

Fysiikassa ekvi­potentiaalin käsitettä käytetään varsinkin sähkö­kentän yhteydessä, mutta sitä voidaan soveltaa muihinkin konservatiivisiin kenttiin,[9] esimerkiksi gravitaatiokenttään.[10] Tällaisissa kentissä työ, joka tehdään hiukkasen siirtyessä pisteessä toiseen, riippuu vain alku- ja loppupisteestä, ei kuljetusta tiestä.[11] Kentässä liikkuvan kappaleen tai hiukkasen potentiaalienergia pysyy vakiona, jos se pysyy samalla ekvi­potentiaali­pinnalla, eikä pelkästään tällä pinnalla liikuttaessa tehdä työtä.

Sähkökentän ekvipotentiaalipinnat

Sähkökentän potentiaali on skalaarikenttä, joka määritellään siten, että sen gradientti kentän jokaisessa pisteessä on suuruudeltaan ja suunnaltaan sama kuin sähkökentän voimakkuus.[12] Kentän kahden pisteen välinen jännite on sama kuin näiden pisteiden potentiaalien erotus. Sähkökentän ekvi­potentiaali­pinnat ovat siis pintoja, joiden pisteiden välinen jännite on nolla. Jos tarkastellaan vain kentän kaksi­ulotteista poikki­leikkausta, ekvipotentiaalit ovat käyriä, ja niitä voidaan verrata topografikarttaan merkittyihin korkeus­käyriin.[8]

Pistemäistä varausta ympäröivän sähkökentän ekvipotentiaali­pinnat ovat samankeskisiä pallopintoja. Jos varaus on tasaisesti jakautunut ohueen sauvaan, sitä ympäröivän kentään kenttä­viivat ovat muodoltaan hyperbelejä ja ekvi­potentiaali­pinnat pyörähdys­ellipsoideja, ja molempien poltto­pisteet ovat sauvan päätepisteissä. Kaukana varauksesta ekvi­potentiaali­pinnat lähestyvät muodoltaan pallo­pintaa, mikäli muita varauksia ei ole läsnä.[7]

Gravitaatiokentän ekvipotentiaalipinnat

Gravitaatiokentässä ekvi­potentiaali­pinnan muodostavat ne pisteet, joissa saman kappaleen potentiaalienergia on yhtä suuri. Tällaiset pinnat ovat kaikkialla kohti­suorassa paino­voiman suuntaa vastaan. Maan paino­voima­kentän ekvi­potentiaali­pinnat ovat muodoltaan lähellä palloa, mutta riittävän pieni osa tällaista pintaa on likipitäen taso, joka määrittelee vaakasuoran suunnan kyseisellä alueella. Vaaka­suoralle tasolle asetettu pallo ei lähde vierimään tasoa pitkin, koska kyseessä on ekvipotentiaalipinta. Erään tärkeän ekvi­potentiaali­pinnan Maan paino­voima­kentässä muodostaa geoidi eli meren pinnan taso ja sen ajatellut jatkeet mantereiden alla.

Kaksois­tähden ympärillä pienin ekvi­potentiaali­pinta, jonka sisään molemmat tähdet jäävät, on kahdeksikon muotoinen Rochen raja. Jos jompi­kumpi tähdistä laajenee siinä määrin, että se ulottuu Rochen rajan ulkopuolelle, siitä vuotaa ainetta myös parin toiseen tähteen.[13]

Ekvipotentiaalinen avaruuden alue

Esimerkin tapauksesta, jossa potentiaali on vakio kokonaisella kolmi­ulotteisella avaruuden alueella, muodostaa ontto pallo ja sen gravitaatio­kenttä. Tällaisen pallon sisäpuolella sen aiheuttama gravitaatio­kenttä on nimittäin kaikkialla nolla, joten sen potentiaali on vakio. Staattisessa sähkö­kentässä jokainen johdekappale muodostaa kolmiulotteisen ekvipotentiaalialueen, koska sen sisällä kentän arvo on kaikkialla nolla. Jos johde­kappale on ontto, kyseessä on Faradayn häkki, jolloin myös sen sisään jäävä alue kuuluu samaan ekvi­potentiaali­alueeseen.

Lähteet
  1. Equipotential Curve Wolfram MathWorld. Wolfram Research. Viitattu 9.10.2015.
  2. Equipotential Lines HyperPhysics. Georgia State University. Viitattu 9.10.2015.
  3. Herman A. Haus, James R. Melcher: ”The Vector Potential and the Vector Poisson Equation”, Electromagnetic Energy. Massachusetts Institute of Technology, 1998. Teoksen verkkoversio.
  4. Leena Lahti: ”Ekvipotentiaalipinnat”, Sähköoppi, s. 26. Gaudeamus, 1977. ISBN 951-662-044-2.
  5. K. V. Laurikainen, Uuno Nurmi, Rolf Qvickström, Erkki Rosenberg, Matti Tiilikainen: ”Jännite ja potentiaali”, Lukion fysiikka 2, s. 32. WSOY, 1974. ISBN 951-0-05657-X.
  6. Pieni tietosanakirja, 3. osa (Masku–Sanomalehti), s. 387. Otava, 1927. Teoksen verkkoversio.
  7. Ismo V. Lindell, Ari Sihvola: Sähkömagneettinen kenttäteoria 1: Staattiset kentät, s. 51. Otatieto, 2007. ISBN 978-951-672-354-2.
  8. Kaarle ja Riitta Kurki-Suonio: ”Skalaariset esitykset”, Vuorovaikutuksista kenttiin: Sähkömagnetismin perusteet, s. 79–80. Limes ry, 1989. ISBN 951-745-121-0.
  9. Daniel L. Lapedes: ”Equipotential surface”, Dictionary of Physics and Mathematics, s. 329. McGraw & Hill, 1978.
  10. Tapio Salmi, Simo Virtanen: ”Voimakentän potentiaalienergia”, Dynamiikka, s. 216. Pressus, 2006. ISBN 952-9835-63-9.
  11. Pieni tietosanakirja, 3. osa (Masku–Sanomalehti), s. 917. Otava, 1927. Teoksen verkkoversio.
  12. Kaarle ja Riitta Kurki-Suonio: ”Yleinen vektoriesitys”, Vuorovaikutuksista kenttiin: Sähkömagnetismin perusteet, s. 81–85. Limes ry, 1989. ISBN 951-745-121-0.
  13. Hannu Karttunen, Pekka Kröger, Heikki Oja, Markku Poutanen: ”Lähekkäisten kaksoistähtien kehitys”, Tähtitieteen perusteet, s. 311. Tähtitieteellinen yhdistys Ursa, Valtion painatuskeskus, 1984. ISBN 951-859-367-1.

    Kirjallisuutta
    • Voipio, Erkki: Sähkö- ja magneettikentät. Moniste 381. Espoo: Otakustantamo, 1987. ISBN 951-672-038-2.
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.