Arkhimedeen spiraali
Arkhimedeen spiraali, joka tunnetaan myös nimellä aritmeettinen spiraali, on muinaiskreikkalaisen matemaatikko Arkhimedeen mukaan nimetty spiraali. Se on niiden pisteiden ura, joiden kautta liikkuva piste kulkee, jos se etääntyy tietystä kiintopisteestä, spiraalin navasta, tasaisella nopeudella pitkin suoraa, joka samanaikaisesti pyörii tasaisella kulmanopeudella saman kiintopisteen ympäri. Napakoordinaatistossa (r, θ) Arkhimedeen spiraalia, jonka napa on origossa, esittää yhtälö

missä a ja b ovat reaalisia vakioita, . Jos parametrin a arvoa muutetaan, spiraali kiertyy napansa ympäri, kun taas parametri b määrittää etäisyyden kahden peräkkäisen kierroksen välillä.
Arkhimedes kuvaili spiraalia teoksessaan Spiraaleista.
Ominaisuuksia
Jokainen Arkhimedeen spiraalin keskuksen kautta kulkeva puolisuora leikkaa spiraalin pisteissä, joiden välinen etäisyys on vakio. Tämä vakio on yhtä kuin 2πb, missä b edellä esitetyssä yhtälössä esiintyvä parametri, kun kulma θ on mitattu radiaaneina. Tähän perustuukin nimitys "aritmeettinen spiraali". Sitä vastoin logaritmisessa spiraalissa nämä etäisyydet, samoin kuin leikkauspisteiden etäisyydet spiraalin keskuksesta muodostavat geometrisen sarjan.
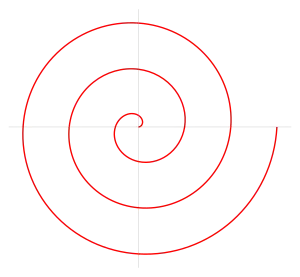
Arkhimedeen spiraali jakaantuu kahteen haaraan, joista toinen vastaan θ:n arvoja θ > 0, toinen arvoja θ < 0. Molemmat haarat kohtaavat toisensa spiraalin keskuksessa. Oheisessa kuvassa on mukana vain toinen haara. Toinen haara saadaan peilaamalla se y-akselin suhteen.
Kuten edellä todettiin, Arkhimedeen spiraali muodostuu, jos piste etääntyy navasta tasaisella nopeudella pitkin puolisuoraa, joka pyörii navan ympäri tasaisella kulmanopeudella. Suurilla θ:n arvoilla eli kaukana navasta piste liikkuu tällöin spiraalia pitkin likimain tasaisella kiihtyvyydellä.[1]
Etäisyys kierrosten välillä
Toisinaan Arkhimedeen spiraalia kuvaillaan spiraaliksi, jonka eri kierrosten välinen etäisyys on vakio. [2] Tarkkaan ottaen tämä on kuitenkin virheellinen luonnehdinta. Kierrosten välinen etäisyys on tosin vakio, jos ne mitataan mitä tahansa spiraalin navasta lähtevää puolisuoraa pitkin, mutta nämä puolisuorat eivät leikkaa spiraalia suorassa kulmassa. Yleensähän etäisyys yhdensuuntaisten suorien tai myös käyrien välillä mitataan sellaista suoraa pitkin, joka leikkaa molemmat kohtisuorasti. On kuitenkin olemassa Arkhimedeen spiraalista jonkin verran poikkeava käyrä, ympyrän involuutta, jonka eri kierrokset tällä tavoin määriteltyinä ovat yhtä kaukana toisistaan.
Yleinen Arkhimedeen spiraali
Joskus nimitystä Arkhimedeen spiraali käytetään myös laajemmasta joukosta spiraaleja, joiden yhtälöt ovat muotoa
Tavallinen Arkhimedeen spiraali saadaan, jos tässä valitaan c = 1. Muita mainittuun laajempaan joukkoon kuuluvia spiraaleja ovat muun muassa hyperbolinen spiraali, Fermat'n spiraali ja lituus.
Esiintyminen luonnossa
Lähes kaikki luonnossa esiintyvät staattiset spiraalit ovat logaritmisia, eivät Arkhimedeen spiraaleja. Sen sijaan monet dynaamiset spiraalit kuten aurinkotuulen Parkerin spiraali tai Katariinan pyöräksi kutsun ilotulitteen muodostama kuvio ovat Arkhimedeen spiraaleja.
Sovelluksia
Pelkästään harpilla ja viivoittimella ei voida neliöidä ympyrää eli piirtää neliötä, jonka pinta-ala olisi tarkalleen yhtä suuri kuin annetun ympyrän. Sen sijaan Arkhimedeen spiraalin avulla se on mahdollista.

Arkhimedeen spiraalilla on useita teknisiä sovelluksia. Scroll-kompressorin, jota käytetään nesteiden ja kaasujen puristamiseen, muodostavat kaksi sisäkkäistä ympyrän involuutan tai käytännössä likimain Arkhimedeen spiraalin muotoista pyörivää kierukkaa.[3] Mekaanisten kellojen jouset ovat yleensä Arkhimedeen spiraalin muotoisia. Sellaisia olivat myös varhaisimpien gramofonilevyjen urat, sillä kun uran eri kierrosten väliset etäisyydet olivat yhtä suuret, saatiin levyn soittoaika tällä tavoin mahdollisimman pitkäksi eli sille saatiin mahtumaan suurin määrä musiikkia. Myöhemmissä levyissä ura kuitenkin muotoiltiin toisin äänen laadun parantamiseksi.[4] Arkhimedeen spiraalia käytetään myös digitaalisessa valonkäsittelyssä, DLP:ssä, "sateenkaari-ilmiön" minimoimiseksi, jotta näyttäsi siltä, että eri värit näkyisivät samaan aikaan, vaikka todellisuudessa punainen, vihreä ja sininen näytetään tulevat näkyviin vuorotellen erittäin nopeasti vaihtuen.[5] Arkhimedeen spiraali muodostuu myös, kun tasapaksu paperi tai kalvo kierretään rullalle lieriön ympärille.[6][7]
Minkä verran ihminen vapisee, voidaan mitata pyytämällä häntä piirtämään Arkhimedeen spiraali. Saatua tietoa voidaan käyttää hyväksi neurologisen sairauksien diagnosoinnissa.
Katso myös
Lähteet
- The On-line Encyclopedia of Integer Sequences, A091154 oeis.org. Viitattu 5.3.2015.
- esim. Julian Havil: Nonplussed! Mathematical Proof of Implausible Ideas, s. 109. Princeton University Press, 2007. ISBN 978-0-691-12056-0.
- Fluid compressing device having coaxial spiral members freepatentsonline.com. Viitattu 5.3.2015.
- Early Development of the LP ronpenndorf.com. Viitattu 5.3.2015.
- Glen Ballou: Handbook for Sound Engineers, s. 1586. CRC Press, 2008. ISBN 9780240809694. Teoksen verkkoversio.
- Joan's Paper Roll Problem mtl.math.uiuc.edu. Arkistoitu 3.11.2013. Viitattu 5.3.2015.
- H. Walser, P. Hilton, J. Pedersen: Symmetry, s. 27. Mathematical Association of America, 2000. ISBN 9780883855324. Teoksen verkkoversio.
Aiheesta muualla
- Jonathan Matt making the Archimedean spiral interesting - Video : The surprising beauty of Mathematics - TED Talks Jonathan Matt. Viitattu 5.3.2015.
- Archimedes' Spiral Erik W. Weisstein, Wolfram Math World. Viitattu 5.3.2015.
- Page with Java application to interactively explore the Archimedean spiral and its related curves groups.dcs.st-and.ac.uk. Viitattu 5.3.2015.
- Online exploration using JSXGraph (JavaScript) jsxgraph.uni-bayreuth.de. Viitattu 5.3.2015.