Arkhimedeen lause

Reaalilukuja koskevan Arkhimedeen lauseen mukaan jokaista reaalilukua r kohtaan löydetään positiivinen kokonaisluku k siten, että

k>r

.

Reaaliluvun B ja kokonaisluvun A suuruudet on ilmaistu janan pituuksilla. Kokonaisluvun A moninkerrat ovat myös kokonaislukuja, joten latomalla peräkkäin lukujen A janoja saadaan lopulta niin pitkä kokonaisluvun nA jana, että se on pitempi jana (luku) kuin reaaliluvun B jana eli lukuina ilmaistuna nA > B.

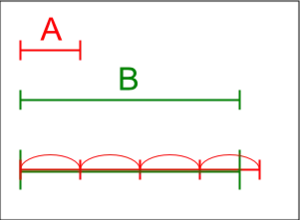
Todistus

Todistetaan ensin, että ylhäältä rajoitetulla kokonaislukujen joukolla on olemassa maksimi. Merkitään tätä joukkoa symbolilla $E$ ja jotain sen ylärajaa symbolilla $B$ , ja määritellään $E=:\{m\in \mathbb {N} \mid m\leq B\}$ . Koska joukko $E$ on ylhäältä rajoitettu, on sillä olemassa täydellisyysaksiooman nojalla pienin yläraja eli supremum, $G=:\sup {E}$ . Supremumin määritelmän mukaan on olemassa joukon $E$ alkio $h$ siten että $G-1/2<h$ . Tällöin $h$ on joukon $E$ maksimi. Mikäli $h$ ei olisi maksimi, niin olisi olemassa kokonaisluku $i\in E$ siten, että $G<h+1\leq i$ . Tämä on ristiriita, koska $j\leq G$ kaikilla $j\in E$ . Täten siis $h$ on joukon $E$ maksimi.

Mikäli $r\leq 0$ , niin 1 on (triviaalisti) haluttu luku $k$ . Oletetaan siis, että $r>0$ . Olkoon nyt joukko $S=:\{l\in \mathbb {N} \mid l\leq r\}$ , jolloin $S$ on ylhäältä rajoitettu. Edellä todistetun lauseen nojalla joukolla $S$ on maksimi. Merkitään $W=:maxS$ ja valitaan $k=:W+1$ . Nyt $k$ ei voi kuulua $S$ :ään, joten $k>r$ .

Arkhimedeen lauseen korollaari: jokaista positiivista reaalilukua $z$ kohtaan on olemassa luonnollinen luku $n$ siten, että $z>1/n$ .

Todistus

Olkoon $z>0$ reaaliluku. Arkhimedeen lauseen nojalla on olemassa luonnollinen luku $n$ siten, että $n>1/z$ , mikä on yhtäpitävää epäyhtälön $z>1/n$ kanssa.

Seurauslauseita

Kahden erisuuren reaaliluvun $a,b\in \mathbb {R}$ välissä on aina rationaaliluku $r$ ja irrationaaliluku $i$ ja molempia vieläpä äärettömän monta eli $a<i<r<b$ .

Todistus

Merkitään $x=:b-a$ . Arkhimedeen lauseen nojalla on olemassa luonnollinen luku $n$ siten, että $x>{\frac {1}{n}}>0$ . Joukolla $E=:\{k\in \mathbb {Z} \mid k\geq nb\}$ on olemassa minimiarvo. Merkitään $p=\min {E}$ . Nyt $p-1$ ei kuulu joukkoon $E$ ja pätee $p-1<nb$ , joka on yhtäpitävää epäyhtälön ${\frac {p-1}{n}}<b$ kanssa. Pätee myös ${\frac {p}{n}}\geq b\implies {\frac {p}{n}}-x\geq b-x=a$ , joten ${\frac {p}{n}}-{\frac {1}{n}}>{\frac {p}{n}}-x\geq a$ . Täten $b>{\frac {p-1}{n}}>a$ ja $r=:{\frac {p-1}{n}}$ on etsitty rationaaliluku.

Osoitetaan, että tällaisia rationaalilukuja on olemassa äärettömän monta. Todistetaan induktiolla, että löydetään halutunlaisia lukuja mikä tahansa lukumäärä $m\in \mathbb {N}$ .

Alkuaskel: edellä todistetun lauseen nojalla on olemassa luku $r_{1}\in \mathbb {Q}$ siten, että $b>r_{1}>a$ .

Induktio-oletus: lukuja, jotka täyttävät ehdon $b>r>a$ , jossa $r\in \mathbb {Q}$ , on olemassa $m-1$ määrä. Tosin sanoen pätee $b>r_{m-1}>r_{m-2}\ \ldots \ r_{1}>a$ .

Induktioaskel: edellä todistetun lauseen nojalla on olemassa luku $r_{m}\in \mathbb {Q}$ siten, että $b>r_{m}>r_{m-1}>a$ .

Täten haluttuja lukuja löydetään $m$ määrä valittiinpa tämä luku miten suureksi tahansa, sillä nyt pätee $b>r_{m}>r_{m-1}>r_{m-1}>r_{m-2}\ \ldots \ >r_{1}>a$ .

Etsitään seuraavaksi lukujen $a$ ja $b$ välistä irrationaaliluku:

Tämä voidaan tehdä monella tavalla. Esimerkiksi edellä todistetun lauseen nojalla löydetään rationaaliluvut $r_{a}\in \mathbb {Q}$ ja $r_{b}\in \mathbb {Q}$ siten, että $b>r_{b}>r_{a}>a$ . Merkitään $s=:r_{b}-r_{a}$ eli $s\in \mathbb {Q}$ . Nyt ilmiselvästi pätee $b>r_{b}>r_{a}+{\frac {s}{\sqrt {2}}}>r_{a}>a$ ja $r_{a}+{\frac {s}{\sqrt {2}}}$ on irrationaaliluku. Yllä olevan kaltaisella induktiolla osoitetaan, että halutunlaisia irrationaalilukuja on olemassa ääretön määrä.

Katso myös

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.