Txikipedia:Koordenatu sistema
Geometrian, puntu bat edo gehiagoren posizioa adierazteko Koordenatu sistema erabiltzen da. Puntu hauen kokalekua erakusteko, Koordenadak erabiltzen dira. Eskolan gehien lantzen den koordenatu sistema, Koordenatu Kartesiarra da, edozein puntu adierazteko erabilgarria dena.
Koordenatu Kartesiarra

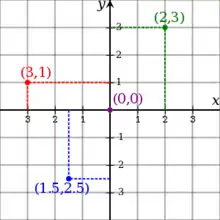
Koordenatu Kartesiarrean bi edo hiru dimentsiotan landu daitezke puntuak, eta honetarako, erabilitako ardatz kopurua aldatuko da.
- Bi dimentsioko puntuak adierazteko, bi ardatz erabiliko dira: X eta Y.
- Hiru dimentsioko puntuak adierazteko, hiru ardatz: X, Y, eta Z.
Bi dimentsiotako puntuak adierazterakoan, X eta Y ardatzetako eskema erabiliko da. X ardatza horizontalki marraztuta dagoen zuzena da (bukaezina) eta aldiz, Y ardatza, bertikalki irudikatutako zuzena. Bi ardatz hauek perpendikularrak dira eta hauek elkartzen direnean, “0” puntua izena hartzen du, (0,0) modura adierazten dena.

X eta Y ardatzak elkar perpendikularrak direnez, eskema lau zati edo koadranteetan banatzen dute, eskuin-goikaldeko kuadrantea 1. koadrantea izanik, ezker-goikaldekoa 2. koadrantea izanik, ezker-behekaldeko koadrantea 3.a izanik eta eskuin-behekaldekoa 4.a.
Bi ardatz hauek gurutzatzen diren puntua ezagututa, (0,0) puntua, ardatzetan marra batzuk agertzen dira, bata bestearen distantzia berdinera kokaturik. X ardatzean, 0 puntutik hasita eskuinaldera joanda, zenbakiek gora egingo dute: 1,2,3,4… eta aldiz ezkerraldera joanda, negatiboki handituko dira: -1,-2,-3,-4… Bestalde, Y ardatzean berbera gertatzen da, marrak sortzen dira bata-bestearen distantzia berdinera. Kasu honetan, 0 puntutik hasita, gorantz joanda zenbakiek gora egingo dute: 1,2,3,4… eta beherantz joanda, negatiboki gora: -1,-2,-3,-4…
Beraz, Plano Kartesiarrak, puntuak adierazteko balio du. Puntuak bi zenbakiz osatuak daude, (-2,5), (4,3) modukoak. Lehenengo zenbakiak X ardatza adierazten du beti, eta bigarrenak, Y ardatza.
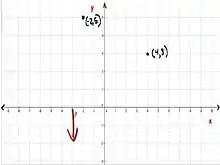
- (-2,5) kasuan, X ardatzan lehenengo zenbakia kokatuko da, kasu honetan -2a, eta Y ardatzan aldiz, bigarren zenbakia, 5a.
- (4,3) kasuan, X ardatzan lehenengo zenbakia kokatuko da, 4a eta Y ardatzan 3a.
Z ardatza
Z ardatza altuera edo sakontasunari dagokio, beti ere goitik begiratuta. Hiru dimentsioetako pieza bat haren neurriekin paper batean marrazteko, soilik bi dimentsio dituelarik, perspektibaz baliatu behar gara, 3D-tako efektua eskuratuz.
Ardatzetako bati makurtasun puntu bat emanda lor daiteke eta hartutako neurriak beste ardatzekiko paraleloak izanda. Modu horretan adibidez, irudi konkretu honen sakontasunaren “Z” ardatzaren neurria O y O\ puntuena izango da.
Hala ere, neurria berdina izaten jarraitzen badu ere, koordenatu sistemaren jatorriaren arabera O eta O\ puntuetako kotak aldatuko dira, “Z_1” eta “Z_2” irudietan ikusi daiteke.
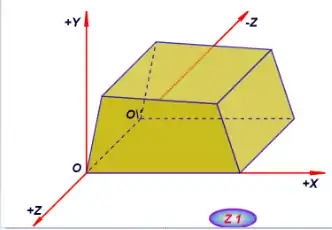 Z_1
Z_1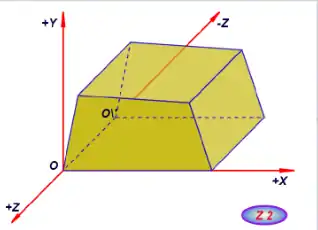 Z_2
Z_2