Teseladun

Teseladuna gainazal laua guztiz estaltzen edo zolatzen duten irudien erregulartasuna edo eredua da. Bi baldintza betetzen ditu:

  1. Hutsunerik ez uztea.
  2. Irudiak ez gainjartzea.
Teseladuna kale bateko espaloian
Solairua apaintzen duen teseladun hexagonala (Erroma)
Tasmaniako penintsulan (Tasmania, Australia) teseladun zoladura naturalaren adibidea.

Hasierako irudi baten kopia isometrikoak erabiliz sortzen dira teseladunak, hau da, azalera guztiz estaltzeko irudiz osatutako pieza edo tesela baten edo gehiagoren kopia berdinak.

Historian zehar kultura ezberdinek teknika hau erabili dute mosaikozko zoladurak edo hormak eratzeko katedraletan eta jauregietan.

  • Zenbait milaka urteko mosaiko sumertarrek erregulartasun geometrikoak dituzte.
  • Arkimedes, K. a. III. mendean, planoa estal dezaketen poligono erregularren inguruko azterketa egin zuen.
  • Johannes Kepler astronomo alemaniarrak planoa estal dezaketen poligono erregularrak aztertu zituen, 1619ko Harmonice mundi lanean. Horrez gain, solido platonikoak deitutakoen hiru dimentsiotako azterketak egin zituen.
  • 1869 eta 1891 artean, Camille Jordan matematikariak, Evgenii Konstantinovitx Fiodorov kristalografoak eta Camila Rial psikologoak planoaren simetriak guztiz aztertu zituzten, horrela teseladunen azterketa sistematikoa eta sakona abiatuz.
  • Gai horretan funtsezko pertsonaia da M.C. Escher (1898-1972) artista herbeheretarra. Bere lagun Harold Coxeter matematikariaren proposamenez, teseladun hiperbolikoak ikasi zituena, eta horrek Granadako Alhambra jauregiarekiko interesa bultzatu zuen. Zenbait artelan eder, bitxi eta misteriotsu sortu zituen.
Erpina partekatzen duten angeluak

Teseladun erregularrak
Artikulu nagusia: «Teseladun erregular»
Triangelu aldeberdinetan oinarritutako teseladuna

Poligono erregularrak dituen teseladun erregularra edo teseladun erregularra poligono erregular mota bakarra erabiltzen duen planoko teseladuna da. Eredu geometriko hauek apaindura helburuetarako asko erabiltzen dira antzinatik.

  • Triangelu aldekideak
    Triangelu aldekideak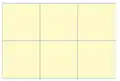
  • Karratuak
    Karratuak
  • Hexagonoak
    Hexagonoak

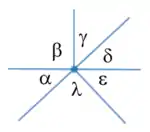
Adibidez: laukiak, 90°ko angeluak dituztenak, erpin bakoitzeko lau sar daitezke eta erpin horren inguruak lauzatu ditzakete.

Teseladun erdi erregularrak

Formazioan poligono erregular bi edo gehiago dituztenak dira.

Teseladun erdi erregular batek propietate hauek ditu:

  1. Poligono erregularrek soilik osatzen dute.
  2. Poligonoen multzoa berdina da erpin bakoitzean.
  3. Zortzi teseladun erdi erregular daude soilik.
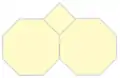  • 4 8 8
    4 8 8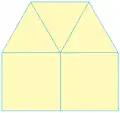
  • 3 3 3 4 4
    3 3 3 4 4
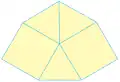  • 3 3 4 3 4
    3 3 4 3 4
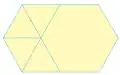  • 3 3 3 3 6
    3 3 3 3 6
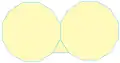  • 3 12 12
    3 12 12
  • 3 4 6 4
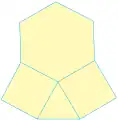    3 4 6 4
  • 3 6 3 6
    3 6 3 6
  • 4 6 12
    4 6 12

Irudi erdi erregularreko teseladunak

  • 4 8 8
    4 8 8
  • 3 3 4 3 4
    3 3 4 3 4
  • 3 3 3 3 6
    3 3 3 3 6
  • 3 12 12
    3 12 12
  • 3 4 6 4
    3 4 6 4
  • 3 6 3 6
    3 6 3 6
  • 4 6 12
    4 6 12

Teseladun irregularrak

Poligono ez-erregularrek osatutakoak dira, baina ez dituzte inoiz lekurik edo pitzadurarik uzten.

Laukiak

Edozein paralelogramo teseladuna egiteko balio du, bere alde paraleloak soilik luzatu behar baitira eta lehenengoarekin bat datozen paralelogramo berriak eraiki behar baitira.

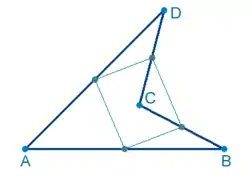
Edozein laukirekin, ahurra edo ganbila izan, posible da azalera laua estaltzea. Kasu ahurrean, erraza da Varignon-en teoremarekin, lauki bakoitzaren erdiko puntuek paralelogramo bat eta gero teseladun bat osatzen dutela frogatzea. Metodo honi sare ikusezinaren metodoa deritzo.

Lauzak Kuadrilateroko Diagrama
Lauzak Kuadrilateroko Diagrama

Triangeluak

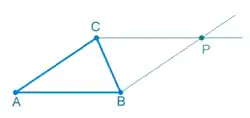
Triangelu eskalenoarekin plano osoa estaltzea posible da. Hori dagokion paralelogramoa osatuz egiaztatzen da. Orokorrean, edozein triangeluk planoa lauzatzen du paralelogramo bat era berean eraikiz.

Planoa lauzatzen duen triangelu diagrama
Planoa lauzatzen duen triangelu diagrama

Hexagonoak

Hexagono erregularrez gain, simetria zentrala duten hexagono ez erregularrek planoa ere lauzatzen dute. Erregularrak ez diren beste hexagono batzuek ez dute planoa lauzatzen.

Kairoko Teseladuna
Kairoko Teseladuna, Egipto.

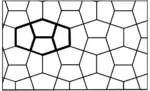
Teseladun hori maiz agertzen da Kairoko kaleetan, Egipton, eta arte islamikoan; hortik dator bere izena. Pentagono horrek bi angelu zuzen ditu, 144°ko angelu bat eta 108°ko bi. Edozein pentagono bezala, bere angeluen batura 540°koa da.

Poligono ahurrak
  • Eskuineko gezia
    Eskuineko gezia
  • Greziako gurutzea
    Greziako gurutzea
  • Himterk angelua
    Himterk angelua
  • Erlaitz gezia
    Erlaitz gezia

Teseladunen eraikuntza

"Kendu, gehitu eta biratu 180°" metodoa

Berez planoa lauzatuko duen irudi geometriko bat marraztean datza, hala nola paralelogramo bat edo triangelu bat. Ondoren, zatiak alde batetik kentzen dira, eta, ondoren, kontrako aldean jartzen dira. Ondoren, irudi hori hainbat aldiz errepikatzen da eta ondo egokitzen diren moduan jartzen dira, transformazio isometrikoak erabiliz (translazioa, biraketa eta simetria)

Isometria

Planoan egiten diren mugimendu edo eraldaketetatik abiatuta, hainbat diseinu lor daitezke.

Erreferentziak

    Kanpo estekak
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.