Solido platoniko
Solido platonikoak (halaber gorputz erregular, gorputz platoniko, gorputz kosmiko, solido pitagoriko edo Platonen poliedro) gorputz geometrikoak dira. Euren ezaugarriak poliedro ganbilak izatea da eta euren aurpegi guztiak poligono erregular berdinak izatea euren erpinetan aurpegi kopuru bera batzen direlarik.
| Poliedroa | Ezaugarriak |
|---|---|
 Tetraedroa | 4 aurpegi 4 erpin 6 ertz |
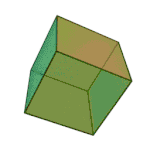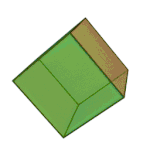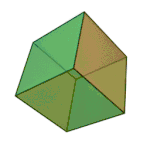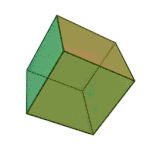 Kuboa edo hexaedroa | 6 aurpegi 8 erpin 12 ertz |
 Oktaedroa | 8 aurpegi 6 erpin 12 ertz |
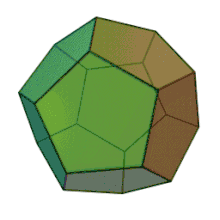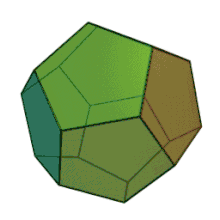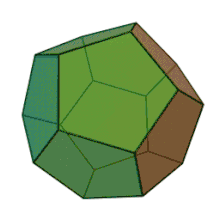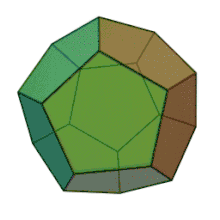 Dodekaedroa | 12 aurpegi 20 erpin 30 ertz |
 Ikosaedroa | 20 aurpegi 12 erpin 30 ertz |
Ezaugarri hauek betetzen dituzten solidoak 5 baino ez dira:
- Tetraedroa.
- Hexaedro erregulara (edo kuboa).
- Oktaedroa.
- Dodekaedroa.
- Ikosaedroa.
Euklidesen Elementuak liburuan jada agertzen dira gorputz hauen inguruko xehetasunak eta Antzinako Grezian izaera magikoa egozten zitzaien. Hainbat filosoforen ustetan "sua tetraedroz osatua zegoen; airea oktaedroz; ura ikosaedroz; lurra kuboz; eta bosgarren forma bat bazegoenez, Jainkoek dodekaedroa erabili zuten ludiaren muga izateko" (Timeoren dialogoa Platonekin.)
Propietateak
Erregulartasuna
- Solido platoniko baten aurpegi guztiak poligono erregular berdinak dira.
- Solido platoniko baten erpin guztiak poligono erregular berdinak dira.
- Solido platoniko baten erpin guztietan ertz eta aurpegi kopuru bera batzen dira.
- Solido platoniko batean dauden aurpegi guztiek sortzen duten angelu diedro guztiak berdinak dira.
Simetria
- Guztiek dute simetria zentral perfektua simetria zentro batekiko, aurpegi guztietatik distantzia berera dagoena.
- Guztiek dute simetria axiala simetria zentrotik pasatzen diren simetria ardatzekiko.
- Guztiek dute ispilu simetria dute.
Guzti honegatik solido platoniko guztiek hiru esfera ezberdinekin harreman bat dute:
- Esfera inskribatu bat, aurpegi guztien zentroekiko tangentea.
- Ertz guztien zentroarekiko tangentea den esfera bat.
- Esfera zirkunskribatu bat, erpin guztietatik pasatzen dena.
Eskema
Eulerren poliedroen teoremak dio poliedro platoniko baten aurpegi (c) kopurua gehi bere erpin (v) kopurua beti dela ertz (a) kopurua gehi bi: