Schwarzschilden metrika

Schwarzschilden koordenatuetan (${\displaystyle t,r,\theta ,\phi }$), ondorengo itxura dauka metrikak:

${\displaystyle g=-c^{2}(1-{\frac {2GM}{c^{2}r}})dt\otimes dt+(1-{\frac {2GM}{c^{2}r}})^{-1}dr\otimes dr+r^{2}(d\theta \otimes d\theta +sin^{2}\phi \;d\phi \otimes d\phi )}$,

non G grabitazio unibertsalaren konstantea, c argiaren abiadura eta M eremu grabitatorioa eragiten duen objektuaren masa diren. ${\displaystyle r=r_{s}={\frac {2GM}{c^{2}}}}$-ri Schwarzschilden erradioa deritzo, eta, ikus daitekeenez, ${\displaystyle r=0}$an eta bertan singularitateak ditugu. Soluzio honek honako bi propietate hauek ditu[1]:

• Asintotikoki laua da. Distantzia infinitura, ${\displaystyle r\rightarrow \infty }$ limitean, Minkowskiren metrika berreskuratzen da (koordenatu polar esferikoetan): eremu grabitatorioa zerora doa infinituan, espero bezala, eta Schwarzschilden koordenatuak infinituan geldi dagoen behatzailearenak dira.
• Estatikoa da: simetria esferikoa duen izar baten azala hedatzen edo uzkurtzen bada ere, kanpoan metrika ez da aldatzen infinituan (r → ∞ limitean) geldi dagoen beha- tzailearen t denborarekin eta, ondorioz, ez du erradiazio grabitatoriorik igortzen. (Gauza bera gertatzen da karga-banaketa esferikoekin: ez dute sortzen erradiazio elektromagnetikorik, nahiz eta erradio aldakorrekoak izan.)

Schwarzschilden soluzioak izena Karl Schwarzschilden omenez du emana, bera izan baitzen 1915ean aurkitu eta 1916an publikatu zuena.[2] Einsteinen erlatibitatearen teoria kaleratu eta oso gutxira lortu zuen. Einsteinen eremu grabitatorioaren ekuazioen lehen soluzio zehatza izan zen, espazio lauaren soluzioaz gain. Schwarzschild bere artikulua publikatu eta gutxira hil zen, Lehen Mundu Gerran zegoela gaixotasun bat harrapatuta.[3]

1916an, Johannes Drostek, bere kabuz, soluzio bera lortu zuen, bide zuzenagoa eta sinpleagoa erabiliz.[4]

Erlatibitatearen teoriaren lehen urteetan nahasmen handia egon zen singularitateen izaera fisikoaren inguruan. Schwarzschildek, bere jatorrizko artikuluan, koodenatu sistemaren hasiera gaur egun gertaera-horizontea deritzogunean ipini zuen.[5] Horrela, ${\displaystyle r=r_{s}}$ eta ${\displaystyle r=0}$-ko singularitateak saihes zitzakeen. Singularitate horiek David Hilbertek aurkitu zituen,[6] hurrengo urtean. ${\displaystyle r=0}$-ko singularitatearen izaera fisikoaren inguruan kontsentsu zabala zegoen. ${\displaystyle r=r_{s}}$-koa, ordea, ez zen ulertzen.[7]

1921ean, Paul Painlevék eta 1922an Allvar Gullstrandek, bakoitzak bere aldetik, Schwarzschild metrikaren koordenatu-aldaketa bat proposatu zuten: Gullstrand–Painlevé koordenatuak. Koordenatu-aldaketa hori eginda, ${\displaystyle r=r_{s}}$-ko singularitatea desagertu egiten zen. Hala ere, ez ziren koordenatu-aldaketa soil bat proposatu zutelaz konturatu. Gainera, Einsteinen teoria oker zegoela arrazoitzen saiatzeko erabili zuten soluzio hura. 1924ean, Arthur Eddingtonek Eddington–Finkelstein koordenatuak proposatu zituen. Horietan ere Gullstran-Painlevé koordenatuetan gertatzen zen gauza bera gertatzen zen. Eddington ere ez zen konturatu, ordea, ${\displaystyle r=r_{s}}$-ko singularitatea koordenatuen araberakoa zela. Hori egiten lehena Georges Lemaître izan zen, Lemaître koordenatuak proposatu zituenean. Singularitate hori fisikoa ez zela esan zuen. 1939an, Howard Robertsonek erakutsi zuen Schwarzschilden metrikan aske erortzen ari zen objektu batek denbora finituan zeharkatuko zuela ${\displaystyle r=r_{s}}$, nahiz eta oso urrun eta geldi legokeen behatzailearentzat inoiz ez zuen egingo.[7]

1960ko hamarkadan egin zen aurrerapen gehiena. Erlatibitatearen teorian geometria diferentziala erabiltzen hasi ziren, eta Lorentzen bariate bat singularra izatea zehazki definitu zen. Horrek ${\displaystyle r=r_{s}}$ gertaera-horizente legez hartzea ekarri zuen.[7]

Schwarzschilden metrika hainbat koordenatutan adieraz daiteke. Koordenatu bakoitzak ezaugarri desberdinak azpimarratzea dakar berarekin. Ondorengo taulak agertzen ditu aukera ohikoenak (${\displaystyle g_{\Omega }=\left(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2}\right)}$):

Koordenatuak	Lerro-elementua	Oharrak	Ezaugarriak
Eddington–Finkelstein koordenatuak (barruranzkoak)	${\displaystyle -\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)\,dv^{2}+2\,dv\,dr+r^{2}\,g_{\Omega }}$		Etorkizuneko horizontean erregularra da. Iraganeko horizontea ${\displaystyle v\rightarrow \infty }$-an.
Eddington–Finkelstein koordenatuak (kanporanzkoak)	${\displaystyle -\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)\,du^{2}-2\,du\,dr+r^{2}g_{\Omega }}$		Iraganeko horizontean erregularra da. Etorkizuneko horizontea ${\displaystyle u\rightarrow \infty }$-an.
Gullstrand–Painlevé koordenatuak	${\displaystyle -\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)\,dT^{2}\pm 2{\sqrt {\frac {r_{\mathrm {s} }}{r}}}\,dT\,dr+dr^{2}+r^{2}\,g_{\Omega }}$		Erregularra da horizonteetan.
Koordenatu isotropikoak	${\displaystyle -{\frac {\left(1-{\frac {r_{\mathrm {s} }}{4R}}\right)^{2}}{\left(1+{\frac {r_{\mathrm {s} }}{4R}}\right)^{2}}}\,{dt}^{2}+\left(1+{\frac {r_{\mathrm {s} }}{4R}}\right)^{4}\,\left(dx^{2}+dy^{2}+dz^{2}\right)}$		Argi-konoak isotropikoak dira denbora konstanteko ebakiduretan.
Krusal-Szekeres koordenatuak	${\displaystyle -{\frac {4r_{\mathrm {s} }^{3}}{r}}e^{-{\frac {r}{r_{\mathrm {s} }}}}\,\left(dT^{2}-dR^{2}\right)+r^{2}\,g_{\Omega }}$		Erregularra da horizontean.
Lemaître koordenatuak	${\displaystyle -dT^{2}+{\frac {r_{\mathrm {s} }}{r}}\,dR^{2}+r^{2}\,g_{\Omega }}$		Erregularra da horizontean.
Koordenatu harmonikoak	${\displaystyle -{\frac {\rho -r_{\mathrm {s} }/2}{\rho +r_{\mathrm {s} }/2}}dt^{2}+{\frac {\rho +r_{\mathrm {s} }/2}{\rho -r_{\mathrm {s} }/2}}d\rho ^{2}+(\rho +r_{\mathrm {s} }/2)^{2}g_{\Omega }}$

Flamm-en paraboloidearen irudia. Bere kurbatura geometrikoa izar esferikoki simetriko baten berdina da.

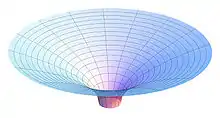
Schwarzschilden soluzioaren espazio-kurbatura ${\displaystyle r>r_{s}}$-rako Flammen parabolaren bidez era egoki batean deskriba daiteke. Horretara heltzeko, denbora konstante hartuta eta ${\displaystyle \theta =\pi /2}$ eginda lortzen den sekzioa aztertu behar dugu, ${\displaystyle (r,\phi )}$ koordenatuek deskribatzen dutena. Inongo esanahi fisikorik ez duen ${\displaystyle w}$ koordenatu euklidearra asmatuko dugu. Orduan, ${\displaystyle (r,\phi )}$ planoan ondorengo ${\displaystyle w}$ txertatzen badugu:

${\displaystyle w=2{\sqrt {r_{\mathrm {s} }\left(r-r_{\mathrm {s} }\right)}}}$

Schwarzschilden metrikan eta plano horretan neurtzen diren distantziak bderdinak dira. Izan ere, planoa hauxe izango da:

${\displaystyle dw^{2}+dr^{2}+r^{2}\,d\phi ^{2}=-c^{2}\,d\tau ^{2}={\frac {dr^{2}}{1-{\frac {r_{\mathrm {s} }}{r}}}}+r^{2}\,d\phi ^{2}}$.

Horregatik, Flammen paraboloidea erabilgarria izango da Schwarzschilden espazio-kurbatura ikusteko. Hala ere, ez da putzu grabitatorio batekin nahastu behar. Partikula batek ere ezingo luke unibertso-lerrorik izan paraboloidearen gainean, distantzia guztiak espazio-motakoak baitira bertan.

Schwarzschilden metrikan, partikula batek orbita zirkular egonkorra izan dezake ${\displaystyle r>3r_{S}}$ denean. Orbita zirkularrak ezegonkorrak izango dira ${\displaystyle 1.5r_{S}}$ eta ${\displaystyle 3r_{S}}$ tartean. ${\displaystyle r<1.5r_{S}}$ kasuan ez da orbita zirkularrik existitzen. Erradio minimoko orbita zirkularrean, abiadura orbitala ia argiaren abiadurakoa izango litzateke.[1]

Schwarzschilden zulo beltza gertaera-horizontea deritzon gainazal irudikariak mugatzen duen eskualdea da. Argiak ere ezin du ihes egin eskualde horretatik, hortik zulo beltz izena. Gertaera-horizontea esfera perfektua da, eta bere zentroan singularitatea dago. Erradioa Schwarzschilden erradioa da. Hain zuzen ere, azken hori da Schwarzschilden zulo beltza ezaugarritzen duen balio bakarra. Geroz eta masa handiagoa izan, Schwarzschilden erradio handiagoa ere izango dugu; hots, zulo beltz handiagoa.[1]