Schrödingerren ekuazioa

De Brogliek bere postulatua argitaratu zuenean, Peter Debye fisikariak pentsatu zuen partikulak uhin bezala funtzionatzen badute, uhin-ekuazio moduko bat bete beharko luketela. Debyeren iradokizunari jarraituz, elektroiarentzat hiru dimentsioko uhin-funtzio apropos bat aurkitzea erabaki zuen Erwin Schrödingerrek. Lan hau aurrera eramateko, William Rowan Hamiltonek aurkeztutako mekanika eta optikaren arteko analogia jarraitu zuen. Bere lanean, sistema optiko batean argiaren  uhin-luzera zerorantz doanean sistema mekaniko baten antza duela aipatzen da, akzio minimoko printzipioa dela eta[2].  Hau da, ekuazio hau garatzeko, fotoien eta eremu elektromagnetikoaren arteko lotura hartu zuen abiapuntu gisa eta materia-uhinen kasura estrapolatu zuen.

1926an, Schrödingerrek bere uhin-ekuazioa aurkeztu zuen[3], gaur egun Schrödingerren ekuazio izenez ezagutzen dena, eta uhin-funtzio baten (ekuazioan ${\displaystyle \Psi (x,t)}$ gisa adierazten dena) denboraren garapena deskribatzen du:

${\displaystyle {\hat {H}}\Psi (x,t)=[-{\frac {\hbar ^{2}}{2m}}{\partial ^{2} \over \partial x^{2}}+V(x,t)]\Psi (x,t)=i\hbar {\partial \over \partial t}\Psi (x,t)}$

Schrödingerren uhin-funtzioa

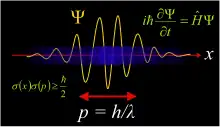
Schrödingerrek, modu oker batean, uhin-funtzioaren moduluaren karratua karga-dentsitate gisa interpretatzen saiatu zen[4][5][6], baina interpretazio arrakastatsua Max Bornek emandakoa izan zen (Bornen legea), uhin-funtzioaren moduluaren karratua probabilitate-dentsitate gisa adierazi zuelako[4].

Urte bat beranduago, 1927an, C. G. Darwinek (biologo famatuaren ilobak) Schrödingerren ekuazioa erabili zuen zenbait egoera ideal aztertzeko[7]. Elektroi aske baten kasuan, adibidez, honi dagokion uhinaren hedapena landu zuen, eta hasierako egoera uhin-fardel gaussiar bat kontuan hartuz, hurrengo adierazpenera iritsi zen:

${\displaystyle x(t)=x_{0}+vt\pm {\sqrt {\sigma ^{2}+({\frac {ht}{2\pi \sigma m}})^{2}}}}$.

Adierazpen honekin v abiadura duen fardel gaussiar baten x posizioa lor daiteke, t denbora igarotakoan (${\displaystyle \sigma }$ hasierako posizioaren ziurgabetasuna da).  Emandako posizioaren ziurgabetasuna dela eta, abiaduran ere ziurgabetasuna agertzen da, eta hemendik Heisenbergen ziurgabetasun printzipiora hel daiteke: ${\displaystyle \Delta x\Delta p\geq {\frac {\hbar }{2}}}$. Hortaz, partikula batek duen uhin-izaera eta honek daukan interpretazio estatistikoa erlazionatuta daudela erakusten du ekuazio honek. Hori dela eta, partikula baten posizioa eta abiadura (edo momentua) ziurtasun osoz jakitea ezinezkoa dela esan daiteke.