Riemannen batura

Izan bitez hauek:

• funtzio bat ${\displaystyle f:[D]\rightarrow \mathbb {R} }$

non D azpimultzo bat den ${\displaystyle \mathbb {R} }$ zenbaki errealen multzoaren barruan

• [a, b] tarte itxi bat D-ren barruan.

• Zenbaki errealen azpimultzo ordenatua eta finitua {x₀, x₁, x₂, ... x_n}, a = x₀ < x₁ < x₂ ... < x_n = b izanik.

Puntu horiek [a, b] tartearen partiketa bat osatzen dute:

P = {[x₀, x₁), [x₁, x₂), ... [x_n-1, x_n]}

Orduan, P partiketa duen [a, b] tartearen gainean definitutako f funtzioaren Riemannen batura honela definitzen da:

${\displaystyle S=\sum _{i=1}^{n}f(y_{i})(x_{i}-x_{i-1})}$

non x_i-1 ≤ y_i ≤ x_i. y_i-ren aukeraketa tarte horretan hautazkoa da.

y_i = x_i-1 baldin bada i guztietarako, orduan S horri Riemannen ezker-batura esaten diogu.

y_i = x_i baldin bada i guztietarako, orduan S horri Riemannen eskuin-batura esaten diogu.

y_i = (x_i+x_i-1)/2 baldin bada i guztietarako, orduan S horri Riemannen erdi-batura esaten diogu.

Riemannen eskuin- eta ezker-baturen batez bestekoa eginez gero, Riemannen trapezoide-batura deiturikoa lortzen dugu

.

Adibidea: ${\displaystyle f(x)=}$x³ funtzioa [0,2] tartearen gainean 4 azpitarteko partiketarekin

Riemannen ezker-batura.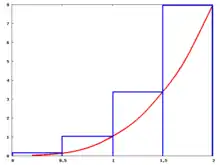

Riemannen eskuin-batura.

Riemannen erdi-batura.

Riemannen trapezoide-batura.

Riemannen integral