Ehuneko

XV. menderako, tresna erabilia zen ehunekoa, batez ere zergak eta interesak kalkulatzeko orduan, baina honen erabilerak aldez aurreko ideia baten laburduran du jatorria. Izan ere, antzinako Erromatar Inperioan, Augusto enperadoreak, enkanteetan saldutako ondasunen gaineko ${\displaystyle {\frac {1}{100}}}$ balioko zerga ordaindu behar zela agintzen zuen zerga-sistema bat ezarri zuen (venalium centesima rerum)[4]. Zatiki horiekin kalkuluak egitea, beraz, ehunekoekin aritzearen baliokidea zen. Ordurako, gainera, kalkuluak errazteko, zatiki sinplifikatuak erabiltzen zitutzen ehunekoetan.

Bestalde, Erdi Aroan diru-izendapenak hazten joan ziren heinean, 100 zenbakidun kalkuluak gero eta estandarizatuagoak bilakatu ziren eta, XV. mendearen bukaera eta XVI. mendearen hasiera bitartean, ohikoa bilakatu zen testu aritmetikoek kalkulu horiek barne hartzea. Testu horietako askok etekina eta galera, interes-tasak eta hiruko erregelarekin erlazionatutako kalkuluetarako aplikatzen zituzten 100 zenbakiarekin erlazionatutako kalkuluak. XVII. mendean, ohikoa bilakatu zen interes-tasak aipatzeko orduan ehunekoak erabiltzea.

Garapena

Ehunekoari erreferentzia egin zion lehenengo sinboloa.

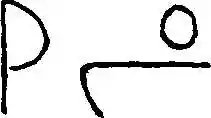
Ehunekoaren ideia zatikien erabilera egunerokotasunean laburtu ahal izateko beharretik sortu zen; izan ere, konplexuagoa zen ${\displaystyle {\frac {2}{3}}}$ kantitateari errefereintzia egitea, % 66 erabiltzea baino eta, beraz, denboraren poderioz ohikoagoa bilakatu zen soilik ehunekoetara murriztutako zatikiez hitz egitea. Gainera, pixkanaka, hitzezko erreferentzia eguneratzen joan zen, "ehuneko" terminora iritsi arte. Hau egitean, kontzeptu honen laburdura islatzeko beharra ere sortu zen, denboran zehar hainbat sinbolo esleituz. Lehena 1425eko eskuizkribu anonimo batetik etorri zen, non egileak garai hartako "ehuneko" hitzari (italierazko «per cento» kontzeptuari, zehazki) erreferentzia egiten zion sinboloa aipatzen zuen (gerora, gaur egungo «%» ikurra bilakatuko zena).

Ehunekeko hitzaren beste hizkuntza batzuetako adierak (per cento, italieraz edota percent, ingelesez, adibidez) latineko per centum hitzetik datoz, nolabait "ehunen bateko multzoa" aduerazi nahi duena. Askotan "per" zatia p. moduan laburtzen zen, eta gerora desagertu egin zen. "cento" zatia lerro horizontal baten bidez banatutako bi zirkulutan banatzen zen, zeinetatik gerora «%» sinboloa eratorri zen.

1425an ehunekoari erreferentzia egin zion lehenengo ikur hartatik gaur egun erabiltzen dugun «%» ikurrera iritsi arte, ordea, ehunekoari erreferentzia egiteko erabilitako sinboloak aldaketa ugari izan ditu urteetan zehar. Askok «%» sinboloa ${\displaystyle {\frac {x}{100}}}$ adierazpen matematikotik abiatuta garatu dela uste dute, baina hori ez da zuzena: «%» sinboloa bi zeroren forma estilizatu bat da. 1425. urteko per cento testuari erreferentzia egiten zion sinbolotik abiatuta, 1650. urtean lerro horizontal bat erakusten zuen sinbolo batera eraldatu zen[5], eta hau izan zen jatorria XVIII. mendean, ikurra bera garatzen joan zen heinean, gaur egun darabilgun «%» ikurra irudikatzera irtsi ziren arte.

Ehunekoaren ikurra XV. mendean	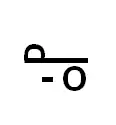Ehunekoaren irudia XVII. mendean	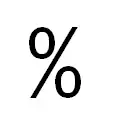Ehunekoaren ikurra XVIII. mendean

Ehunekoaren ikurraren erabilera hizkuntzaren arabera aldatzen da. Honela, hizkuntza batzuetan, euskara kasu, zenbakiaren aurretik jartzen da (ehuneko 5 esaten delako); ingelesez, gaztelaniaz edo frantsesez ondoren jartzen da (5%). Espazioaren erabilera ere aldatzen da hizkuntzaren arabera, batzuetan jartzen da, eta beste batzuetan ez. Hala ere, ISO 31-0 arauak gomendatzen du espazio bat jartzea ikurraren eta zenbakiaren artean[6][7].

Ehuneko balioa kalkulatzeko, proportzioaren zenbakizko balioa 100 zenbakiarekin biderkatu behar da. Adibidez, demagun 50 sagarrek 1250 sagarreko multzoan osatzen duten ehunekoa kalkulatzeko, proportzioa kalkulatu eta 100 zenbakiarekin biderkatuz lortuko dugu: ${\displaystyle {\frac {50}{1250}}\cdot 100=0,04\cdot 100=\%\;4}$.

2009 eta 2012 artean Wikimedia guneak bisitatzeko web nabigatzaileetako bakoitzari dagokion erabilera-maiztasunaren ehunekoa

Bestalde, ehuneko baten ehunekoa klakulatzeko, bi horiek 100 zenbakiaren frakzio moduan edo zenbaki hamartar gisa adierazi behar dira, eta ondoren bata bestearekin biderkatu. Adibidez, demagun % 60aren %30a hurrengo eran kalkulatu beharko litzateke:

${\displaystyle {\frac {60}{100}}\cdot {\frac {30}{100}}=0,60\cdot 0,30=0,18={\frac {18}{100}}=\%18}$

Garrantzitsua da konturatzea ezin dela aldi berean 100 zenbakiaz zatitu eta «%» ikurra erabili; hau da, bata bestearen baliokidea da, eta aldi berean erabiltzeak 100 zenbakiagatik bi aldiz zatitzea adierazten du. Adibidez, ehuneko hogeita bosta adierazteko hurrengo hiru adierazpenak zuzenak eta baliokideak dira: ${\displaystyle \%\;25={\frac {25}{100}}=0,25}$. Aldiz, ${\displaystyle {\frac {\%\;25}{100}}}$ez da zuzena, hurrengoa adierazten baitu: ${\displaystyle {\frac {\%\;25}{100}}={\frac {\frac {25}{100}}{100}}={\frac {0.25}{100}}=0.0025}$. Aldi berean, ${\displaystyle \%\;{\frac {100}{100}}}$adierazpena ere okerra izango litzateke asmoa % 100 adieraztea denean, aurreko adierazpenarekin % 1 irakurriko litzateke eta.

Ehunekoekin kalkuluak egiteaz gain, garrantzitsua da jakitea ehuneko bati buruz hitz egiten denean, zerekiko den erlatiboa (hau da, zeinden %100ari dagokion guztizkoa). Hori hurrengo probleman aztertu daiteke:

Unibertsitate jakin batean, ikasle guztien % 60 emakumeak dira, eta ikasle guztien % 10 informatikako ikasleak dira. Emakume ikasleen % 5 informatikako ikasleak badira, guztira informatikako ikasleen zein ehuneko dira emakumeak?

Kasu honetan, informatikako ikasleen artean emakumeei dagokien proportzioa kalkulatzeko eskatzen digute. Badakigu ikasle guztien % 60 emakumeak direla, eta horien artean % 5 informatikako ikasleak direla. Hortik hurrengoa ondoriozta dezakegu: ikasle guztien artean, informatika ikasten duten emakumeak ${\displaystyle {\frac {60}{100}}\cdot {\frac {5}{100}}=0,60\cdot 0,05=0,03={\frac {3}{100}}=\%3}$ dira. Bestalde, badakigu ikasle guztien artean % 10a bakarrik direla informatikako ikasleak (gizonak nahiz emakumeak), eta beraz, informatikako ikasleen artean emakumeei dagokien proportzioa kalkulatzeko hurrengo zatiketa egin behar da: ${\displaystyle {\frac {\%\;3}{\%\;10}}={\frac {30}{100}}=\%30}$, eta horixe litzateke problemaren emaitza: Informatikako ikasle guztien artaen, %30 dira emakumeak.

Kantitate batean "% x-ko igoera" edo "% x-ko jeitsiera" aipatzen denean, ohiko interpretazioa da aldaketa kantitate horren hasierako balioarekiko erlatiboa dela. Orokorrean:

• Kantitate batean ehuneko x-ko igoera dagoela esaten denean (% x), bukaerako kantitatea hasierakoaren ehuneko 100 + x da: % (100 + x), edo baliokidea dena: (1+ 0,01x) aldiz hasierako kantitatea.
• Kantitate batean ehuneko x-ko jeitsiera dagoela esaten denean (%x), bukaerako kantitatea hasierakoaren ehuneko 100 - x da: % (100 - x), edo baliokidea dena, (1 - 0,01x) aldiz hasierako kantitatea.

Hurrengoak, ehuneko igoera eta jeitsieren adibide batzuk dira:

• Hasierako kantitatean % 60ko igoera bat izateak esan nahi du bukaerako kantitatea hasierakoaren %160 dela, edo 1,6 aldiz hasierakoa.
• Hasierako kantitatean %100eko igoera bat izateak esan nahi du bukaerako kantitatea hasierakoaren %200 dela, edo 2 aldiz hasierakoa. Hortaz, kasu honetan hasierako kantitatea bikoiztu egiten da.
• Hasierako kantitatean %60ko jeitsiera bat izateak esan nahi du bukaerako kantitatea hasierakoaren %40 izango dela, edo 0,4 aldiz hasierakoa.
• Hasierako kantitatean %100eko jeitsiera bat izateak esan nahi du bukaerako kantitatea zero izango dela.
  

• Ehuneko-puntuak
• Oinarri-puntuak