Plastikotasun
Plastikotasuna iraunkorki eta itzulezin deformatzeko gaitasuna duten material anelastiko batzuen portaera mekaniko bereizgarria da beren tarte elastikotik gorako tentsioak jasaten dituztenean, hau da, beren muga elastikotik gora.
Metaletan, plastikotasuna dislokazioen desplazamendu itzulezinei dagokienez azaltzen da.
Sarrera
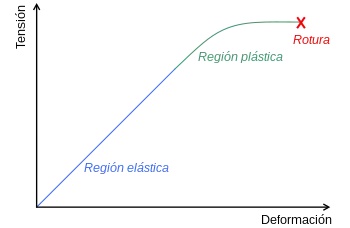
Material elastikoetan, bereziki metal harikor askotan, trakzio-esfortzu ardatz-bakar txiki batek portaera elastikoa dakar. Horrek esan nahi du trakzio-esfortzuaren igoera txikiek deformazioaren gehikuntza txikiak ekartzen dituztela, karga berriro zero bihurtzen bada gorputzak bere jatorrizko forma zehatza berreskuratzen du; hau da, deformazioa guztiz itzulgarria da. Hala ere, esperimentalki egiaztatu da muga bat dagoela, muga elastikoa deritzona; tentsioen funtzio homogeneo jakin batek muga hori gainditzen badu, deformazio hondarrak geratzen dira karga desagertzen denean, eta gorputza ez da zehatz-mehatz bere formara itzultzen. Hau da, deformazio itzulezinak agertzen dira.
Goian deskribatutako portaera elasto-plastiko mota hori metal ezagun gehienetan aurkitzen da, baita beste material askotan ere. Jokaera guztiz plastikoa ez da hain ohikoa, eta deformazio itzulezinak agertzea dakar tentsioa txikia izan arren; modelatzeko buztina eta plastilina portaera guztiz plastikora hurbiltzen da. Beste material batzuek, gainera, gogortze plastikotasuna erakusten dute, eta gero eta tentsio handiagoak behar dituzte beren deformazio plastiko osoa handitzeko. Aurreko jokabideak efektu likatsuekin batera etor daitezke, tentsio-tasa handien kasuan tentsioak handiagoak izatea eragiten dutenak; portaera horri bisko-plastikotasuna deritzo.
Materialen plastikotasuna material horien aldaketa itzulezinekin lotuta dago. Termodinamikoki itzulgarria den portaera elastikoa ez bezala, plastikoki deformatzen den gorputz batek entropia-aldaketak jasaten ditu, hala nola dislokazio-aldaketak. Portaera plastikoan, energia mekanikoaren zati bat barrutik xahutzen da energia potentzial elastiko bihurtu beharrean.
Mikroskopikoki, metalen kristal-sarearen eskalan, plastikotasuna dislokazio izeneko sarean, zenbait inperfekzio egotearen ondorioa da. 1934an, Egon Orowan-ek, Michael Polanyi-k eta Geoffrey Ingram Taylor-ek, gutxi gorabehera aldi berean, ondorioztatu zuten material harikorren deformazio plastikoa dislokazioaren teoriaren arabera azal zitekeela. Plastikotasuna deskribatzeko, deformazio-tentsore eta tentsio-tentsore osagaien aldaketak deskribatzen dituen ekuazio diferentzial ez-lineal eta denboraren mendeko multzo bat erabili ohi da, aurreko deformazio- eta tentsio-egoerarekiko eta une bakoitzeko deformazio-gehikuntza.
Plastikotasunaren historia
XIX. mendean Tresca, Saint-Venant, Lévy eta Bauschinger-en lanekin finkatu zen plastikotasunaren teoria modernoaren oinarria. XX. mendearen hasieran, zenbait aurrerapen eman zituzten Prandtl, Von Mises eta A. Reuss-ek fenomenoaren ulermenean. Lehen fase horretan, deformazio itzulezina, hutsegite irizpideak, gogortzea eta plastikotasun perfektuaren kontzeptua sartu ziren, baita deformazio plastikoaren ekuazio eratzaileen gehikuntza forma ere.
Bigarren Mundu Gerraren ostean, Prager, Drucker eta Hill-en lanak agertu ziren, non formulazioaren argitasun handiagoa lortu eta azalaren isurpen ganbiltasuna ezarri zen. Handik gutxira, 1960ko hamarkadan hasita, ekuazio diferentzial partzialen eta aldaera-desberdintasun teoriaren zenbait aurrerapen matematiko eman ziren, plastikotasunaren teoriarako bereziki lagungarriak izango zirenak. Aurrerapen horiek frogatu zuten solido elastoplastikoen hasierako balio-arazoak ebazteko marko naturala desberdintasun aldaerak zirela. Solidoen mekanika eta matematika alorreko zenbait aurrerapen bat egiteak garapen teoriko berriak sortu zituen, eta horien adibide dira Moreauren artikuluak, Duvauten monografiak eta J.L Lions eta Temam.
Plastikotasun ereduak
Oro har, plastikotasun-eredu batek hainbat elementu definitzea eskatzen du:
- Lehenik eta behin, tentsio nagusien espazioan, tentsio onargarrien eremua deritzona definitu behar da, tentsio-espazio horren multzo itxia (eta, agian, trinkoa) izango dena. Multzo horren mugari, etekin-azalera deitu ohi zaio.
- Esfortzu nagusiak, tentsio onargarrien eskualdean dauden solidoaren puntuetarako, portaera elastikoa da. Dena den, errendimendu-azaleko puntuetarako, beharrezkoa da fluxuaren araua definitzea, zeinak deformazio plastikoa nola handituko den (tentsioaren gehikuntza-tasa eta beste barne-parametro batzuen arabera) bere isurpen puntura iritsi den material baten tentsioa gehitzen bada.
- Plastikotasun inperfektuaren ereduek eskatuko dute tentsio-eremu onargarria denboran zehar gogortzea eta desplazatzea kontuan hartzen duten barne-aldagaien multzoa definitzea gainerako aldagaien gehikuntza-tasen arabera.
Barne-aldagaiak egoteak —esaterako, plastifikazio-maila (deformazio plastikoa), gogortzea eta beste— tentsioen eta deformazioen arteko erlazioa kasu elastikoan baino konplexuagoa bihurtzen du; bereziki, barne-aldagaiak nola aldatu diren jakin ezean, deformazio-esfortzu elastikoen maila kontuan hartuta ezin dira tentsioak jakin. Barne-aldagaiak nola aldatzen diren kontuan hartzeak esan nahi du problema elastoplastiko bat, orokorrean, problema dinamiko gisa unibokoki ebatz daitekeela sistema honen ekuazioak aldi berean ebatziz:
non lehen erlazioak tentsio mekanikoaren arteko ekuazio eratzailea adierazten duen (), deformazioak (), barne aldagaiak (), solidoaren puntu bakoitzeko. Bigarren erlazioa barneko esfortzuen eta aplikatutako indarren arteko indar oreka biltzen duen deribatu partzialetako ekuazioa da (), eta azkena ekuazio diferentzial arrunta da, barne-aldagaiak (bereziki deformazio plastikoa) denborarekin nola handitzen diren adierazten duen fluxu-araua ematen duena ekuazio diferentzial arrunta materiala tentsio-egoerara iristen denean, non isurpena agertzen den.
Tentsio-deskonposizioa
Material plastiko baten deskribapenak deformazio osoa deskribatzen duten aldagaiak eta barne aldagaiak behar ditu. materialaren barruan gertatzen diren aldaketa atzeraezinak deskribatzen dituztenak. Aldagai horiek materialaren xahutze-erlazioetan ere esku hartzen dute. Kontsiderazio termodinamikoek daramate Gibbsen energia askea g (bolumen unitateko) Helmholtz energia askearekin f, , tentsioak deformazioak erlazionatuta egotera erlazio honen bidez:
Non:
- Gibbs energia askea eta Helmhotz energia askea bolumen unitateko,
- tentsio-tentsorearen osagaiak dira;
- deformazio-tentsorearen osagaiak dira, eta
- materialaren aldaketa itzulezinekin lotutako barne-aldagaien multzoa dira
Aurreko erlazioak honakoa dakar:
(*)
Esperimentalki jakina da betetze tentsorea ez dirudiela deformazio plastikoaren prozesu itzulezinek eragiten duenik, eta horrek esan nahi du:
Eta kasu horretan, tentsioaren deskonposizio gehigarria gertatzen da, tentsio elastikoan eta tentsio plastikoan, zeren -ren deformazio plastikoaren independentziaren hipotesiaren arabera ( forma honetan integra daiteke:
Bestalde, fluxu-legea energiaren xahupen plastikoarekin lotutako desberdintasun batek mugatzen du. Desberdintasun hau termodinamikaren bigarren legetik dator Clausius-Duhem forman:
Non:
- Helmholtz energia librea eta bolumen unitateko entropia dira.
- gainazaleko tenperatura eta bero-fluxua dira.