Mollweiden formulak

Trigonometrian, Mollweiden formulak, edo antzinako testu batzuetan Mollweiden ekuazioak, Karl Mollweiden omenez izendatuak, triangeluaren aldeen eta angeluen arteko erlazio batzuk dira.[1][2] Triangeluen bazpenaren emaitza egiaztatzeko erabil daitezke.[3]

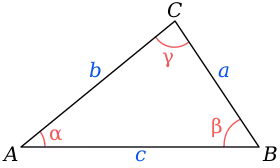
Triangelu bat. α, β eta γ angeluak a, b eta c aldeen aurkakoak dira, hurrenez hurren.

Izan bitez a, b eta c triangelu baten hiru aldeen luzerak, eta α, β eta γ haien aurkako angeluen neurriak, hurrenez hurren. Mollweiden formulak hauek dira:

${\displaystyle {\frac {a+b}{c}}={\frac {\cos \left({\frac {\alpha -\beta }{2}}\right)}{\sin \left({\frac {\gamma }{2}}\right)}}}$

eta:

${\displaystyle {\frac {a-b}{c}}={\frac {\sin \left({\frac {\alpha -\beta }{2}}\right)}{\cos \left({\frac {\gamma }{2}}\right)}}.}$

Identitate horietako bakoitzak triangeluaren sei neurri erabiltzen ditu: hiru angeluak eta hiru aldeetako luzerak.