Mekanika klasikoaren kronologia

Mekanika klasikoaren kronologia edo denbora-lerroa bi garaitan banatu ohi da, Newton baino lehenagokoa (mekanika goiztarra) eta Newtonen ondorengoa (mekanika newtondarra):[1]

Artikulu sorta honen partea:
Mekanika klasikoa
Newtonen legeak
Adarrak
Oinarriak
Zientzialariak
Muinekoak
Biraketa
Formulazioak
Kategoriak
Mekanika klasikoa

Mekanika goiztiarra
  • K.a. IV. mendea - Aristotelesek fisika aristoteliarraren sistema asmatu zuen, gerora neurri handi batean gaitzetsi dena
  • K.a. IV. mendea - Babiloniar astronomoek Jupiterren posizioa kalkulatu dute Batezbesteko abiaduraren teorema erabilita [2]
  • K. a. 260 - Arkimedesek palankaren printzipioa lantzen du eta Arkimidesen printzipioa finkatzen du, hau da, fluido batean sartutako objektu orok, desplazatutako fluidoaren pisu bereko indar bertikala jasatzen duela gorantz.
  • 60 - Alexandriako Heronek Metrica, Mekanika (objektu astunak altxatzeko bitartekoak) eta Pneumatika (presio bidez lan egiten duten makinez) idazten ditu
  • 350 - Themistiosek dio marruskadura estatikoa marruskadura zinetikoa baino handiagoa dela
  • VI. mendea - John Philoponus-ek dioenez, behaketaren arabera, oso pisu desberdina duten bi bola abiadura berdinean eroriko dira. Beraz, baliokidetasun printzipioa probatzen du
    Taula, Fisikaren Historia 500-900 (UEU, 1990)[1]
  • Al-Biruni
    1021 - Al-Birunik hiru koordenada ortogonal darabiltza espazioko puntuak deskribatzeko
  • 1000-1030 - Alhazen-ek eta Avicena-k inertzia eta momentu kontzeptuak garatzen dituzte
  • 1100-1138 - Avempazek erreakzio-indarraren kontzeptua garatzen du [3]
  • 1100-1165 - Hibat Allah Abu'l-Barakat al-Baghdaadik deskubritzen du indarra azelerazioarekin proportzionala dela eta ez abiadurarekin, mekanika klasikoan funtsezko legea dena
  • Ptolomeoren eredu geozentrikoa. Eta Kopernikoren eredu heliozentrikoa (1543)[1]
    1121 - Al-Khazini-k Jakintza-orekaren liburua argitaratzen du, distantzia batean dagoen grabitatearen kontzeptuak garatzen dituena. Iradokitzen du grabitatea unibertsoaren erdigunera dagoen distantziaren arabera aldatzen dela, hau da, Lurrarekiko distantzia [4]
  • 1340-1358 - Jean Buridanek bultzadaren teoria garatzen du
  • XIV. mendea - Oxfordeko kalkulatzaileek Frantziako kolaboratzaileekin batezbesteko abiaduraren teorema frogatzen dute
  • XIV. mendea - Nicole Oresmek denboraren karratuaren legea asmatzen du era uniformean azeleratutako aldaketa deskribatzeko.[5] Hala ere, Oresmek aurkikuntza hau ariketa intelektual hutsa zela esan zuen, fenomeno naturalen deskribapenerako inolako garrantzirik ez zuena, eta ondorioz ezin izan du inolako loturarik ezagutu azeleratutako gorputzen mugimenduarekin[6]
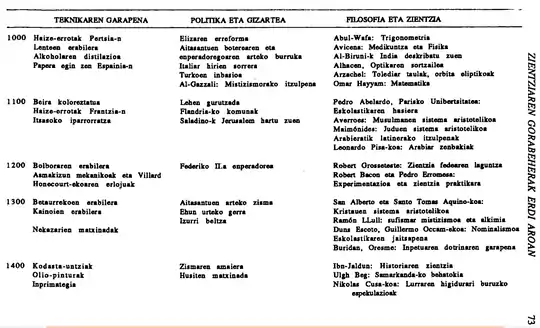    Taula, Fisikaren Historia 1000-1400 (UEU, 1990)[1]
  • 1500-1528 - Al-Birjandi-k "inertzia zirkularraren" teoria garatzen du Lurraren biraketa azaltzeko[7]
  • XVI. mendea - Francesco Beato eta Luca Ghini modu esperimentalean eroriko askearen ikuspegi aristoteliarraren kontraesanak aurkitzen dtuzte[8]
  • XVI. mendea - Domingo de Soto-k iradokitzen du euskarri homogeneo batean zehar erortzen diren gorputzak uniformeki azeleratzen direla.[9][10] Sotok, hala ere, ez zuen aurreikusi Galileok erortzen diren gorputzen teorian jasotako kualifikazio eta hobekuntza asko. Ez zuen ulertu, esate baterako, Galileok egin zuen bezala, gorputz bat ingurune hutsean soilik eroriko zela azelerazio guztiz uniformearekin, eta bestela azkenean abiadura uniforme batera iritsiko zela.
  • Galileo Galilei
    1581 - Galileo Galilei penduluaren erloju-mugimenduaz ohartu zen
  • 1589 - Galileo Galileik plano inklinatuetan jaurtitzen dituen pilotak erabiltzen ditu pisu desberdinak azelerazio berarekin erortzen direla erakusteko
  • 1638 - Galileo Galileik Bi zientzia berriri buruzko elkarrizketak argitaratu ditu (materialen zientzia eta zinematika) non, besteak beste, Galileleoren eraldaketa garatzen den
  • 1645 - Ismaël Bullialdusek defendatzen du "grabitatea" ahuldu egiten dela distantziaren karratuaren inbertsoaren arabera [11]
  • 1651 - Giovanni Battista Riccioli eta Francesco Maria Grimaldik Coriolis efektua deskubritzen dute
  • 1658 - Christiaan Huygensek esperimentalki deskubritzen du alderantzizko zikloide baten barruan kokatutako pilotak aldi berean zikloidearen punturik baxuenera iristen direla eta horrela esperimentalki erakusten du zikloidea tautokronoa (kurba isokrona) dela
  • 1668 - John Wallisek momentu linealaren kontserbazioaren legea iradokitzen du
  • 1676-1689 - Gottfried Leibnizek vis viva kontzeptua garatzen du, energiaren kontserbazioaren printzipio mugatua

Mekanika klasikoaren eraketa (batzuetan mekanika newtondarra deritzo)

Erreferentziak
  1. Etxebarria Bilbao, Jose Ramon; Ensunza Lekunberri, Martxel; Egiguren Ganboa, Josu; Ugalde Lorda, Patxi; Lasa Iguain, Iñaki; Salazar Ruiz, Arantzazu; Uraga Laurrieta, Bittor; Urain, Jose Luis. (). Fisikaren historia laburra. UEU ISBN 978-84-86967-27-7. (Noiz kontsultatua: 2020-05-01).
  2. (Ingelesez) Ossendrijver, Mathieu. (2016-01-29). «Ancient Babylonian astronomers calculated Jupiter’s position from the area under a time-velocity graph» Science 351 (6272): 482–484.  doi:10.1126/science.aad8085. ISSN 0036-8075. PMID 26823423. (Noiz kontsultatua: 2020-05-01).
  3. Shlomo Pines (1964), "La dynamique d’Ibn Bajja", in Mélanges Alexandre Koyré, I, 442-468 [462, 468], Paris.
    (cf. Abel B. Franco (October 2003). "Avempace, Projectile Motion, and Impetus Theory", Journal of the History of Ideas 64 (4), p. 521-546 [543]: "Pines has also seen Avempace's idea of fatigue as a precursor to the Leibnizian idea of force which, according to him, underlies Newton's third law of motion and the concept of the "reaction" of forces.")
  4. Mariam Rozhanskaya and I. S. Levinova (1996), "Statics", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. 2, p. 614-642 [621], Routledge, London and New York
  5. Clagett (1968, p. 561), Nicole Oresme and the Medieval Geometry of Qualities and Motions; a treatise on the uniformity and difformity of intensities known as Tractatus de configurationibus qualitatum et motuum. Madison, WI: University of Wisconsin Press. ISBN 0-299-04880-2.
  6. Grant, 1996, p.103).
  7. F. Jamil Ragep (2001), "Tusi and Copernicus: The Earth's Motion in Context", Science in Context 14 (1-2), p. 145–163. Cambridge University Press.
  8. «Timeline of Classical Mechanics and Free Fall» www.scientus.org (Noiz kontsultatua: 2020-05-01).
  9. Sharratt, Michael (1994). Galileo: Decisive Innovator. Cambridge: Cambridge University Press. ISBN 0-521-56671-1, p. 198
  10. Wallace, William A. (2004). Domingo de Soto and the Early Galileo. Aldershot: Ashgate Publishing. ISBN 0-86078-964-0 (pp.II 384, II 400, III 272)
  11. Ismail Bullialdus, Astronomia Philolaica … (Paris, France: Piget, 1645), page 23.
  12. Poinsot (1834) Theorie Nouvelle de la Rotation des Corps, Bachelier, Paris
  13. (Ingelesez) Parker, Eugene N.. (1954-12-15). «Tensor Virial Equations» Physical Review 96 (6): 1686–1689.  doi:10.1103/PhysRev.96.1686. ISSN 0031-899X. (Noiz kontsultatua: 2020-05-01).
  14. V. I. Arnold, Mathematical Methods of Classical Mechanics, Graduate Texts in Mathematics (Springer, New York, 1978), Vol. 60.

Kanpo estekak
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.