Maxwell-Boltzmann banaketa
Fisikan (bereziki mekanika estadistikoan), Maxwell-Boltzmann banaketa honako hau da: James Clerk Maxwell eta Ludwig Boltzmann-en izena duen probabilitate banaketa partikularra.
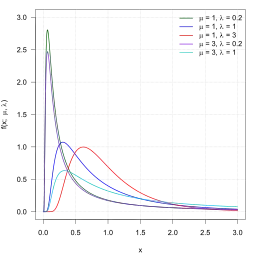
Lehendabizi, gas idealetan partikulen abiadura deskribatzeko erabili zen, partikulak edukiontzi baten barruan askatasun osoz mugitzen baitira inolako elkarrekintzarik izan gabe, elkarren arteko energia eta bultzada elkarren artean edo bere ingurune termikoarekin trukatzen dituzten bat-bateko talkak izan ezik. Esan beharrekoa da, testuinguru honetan “partikula” hitzak partikula gaseosoei egiten diela erreferentzi bakarrik (atomoei eta molekulei). Honez gain, partikulen sistema oreka termodinamikoan[1] dagoela suposatzen da. Partikula horien energiek Maxwell–Boltzmannen distribuzioa deritzonari jarraitzen diote, eta abiaduren banaketa estatistikoa, partikulen energiak eta energia zinetikoa berdinduz lortzen da.
Berez, matematikoki, Maxwell-Boltzmann banaketa hiru askatasun graduko X (chi) distribuzioa da (abiadura bektorearen osagaiak espazio euklidear batean), abiadurak neurtzen dituen parametro eskala batean. Abiadura horien unitateak honako zatiketa honen unitateen proportzionalak dira:
Non, T tenperatura eta m masa diren[2].
Maxwell-Boltzmann distribuzioa gasen teoria zinetikotik ondorioztatu zen. Teoria honek, oinarrizko propietate gaseoso asko azaltzen ditu modu sinplifikatuan, presioa edota difusioa batik bat[3]. Maxwell-Boltzmann banaketa, funtsean, hiru dimentsioko partikulen abiadureei aplikatzen zaien arren, partikulen abiaduraren moduluaren menpe baino ez dago. Probabilitate banaketak ea zein abiadura den probableena adierazten du. Partikulek distribuziotik ausaz aukeratutako abiadura izango dute, baina probabilitate handiagoa izango dute tarte batean dauden abiadurak izateko beste batzuetakoak baino. Gasen teoria klasikoa, aldiz, gas idealetarako erabiltzen da, baina, egia esan, gas horiek gas errealen idealizazio bat baino ez dira. Benetako gasetan, Maxwell-Boltzmannen formaren desberdina den abiadura banaketa izan dezakete gasek, hainbat efekturen ondorioz (esate baterako, Van der Waalsen indarrak). Dena dela, dentsitatea txikiagotuta daukaten gasek gas idealen antzera jokatzen dute. Ondorioz, Maxwell-Boltzmann distribuzioa hurbilketa erabilgarria da gas horientarako[4].
Distribuzioa Maxwellek proposatu zuen lehenengo aldiz 1860ean[5]. Hamar urte beranduago, Boltzmannek Maxwellek proposatutako lana osatu zuen, distribuzioen esanahi fisikoa zein zen proposatuz.
Banaketa funtzioa
Intereseko sistemak partikula kopuru handia daukala suposatuz, hiru dimentsioko abiadura espazioaren elementu infinitesimal baten barruan dauden partikulen frakzioa, magnitudeko abiadura bektore batean zentratua, da, non
den, partikularen masa, Boltzmannen konstantea eta T tenperatura termodinamikoa izanik.
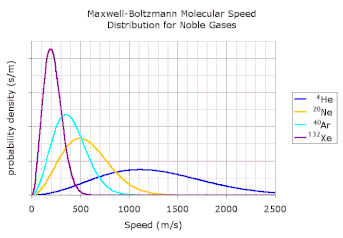
Abiadura espazioko elementua gisa idatzi daiteke koordenatu kartesiarretan edo koordenatu esferikoetan, non angelu solidoaren elementua den. banaketa funtzioa dela jakinik, funtzioa normalizatzean izango da espazio osoan integratuz.
Goiko funtzioa bi dimentsiotan integratuz eta -rekiko, banaketa funtzio Maxwelliarra eskuratu dezakegu norabide bakarrean higitzen diren partikulen sisteman. Norabidea bada
sistema isotropikoa denez, angelu solidoarekiko integratu daiteke eta probabilitate banaketa hurrengo funtzio gisa idatzi[6]
Probabilitate dentsitate honek partikula batek abiadura izateko duen probabilitatea ematen du. Maxwell-Boltzmannen banaketa chi banaketaren baliokidea da hiru askatasun gradurekin eta eskala parametroarekin.
Banaketak betetzen duen ekuazio diferentzial arruntena hurrengo hau da:
edo unitate gabeko presentazioa erabiliz:
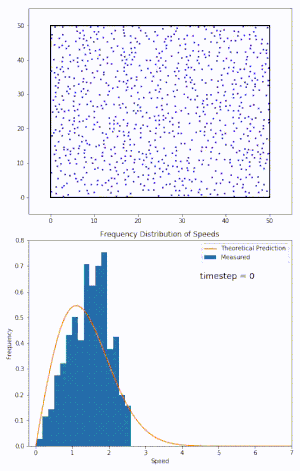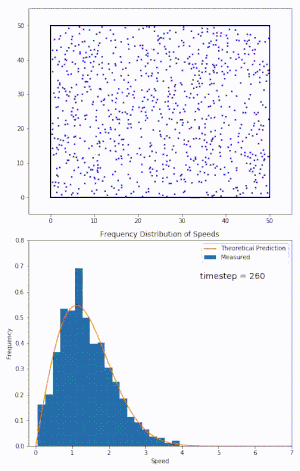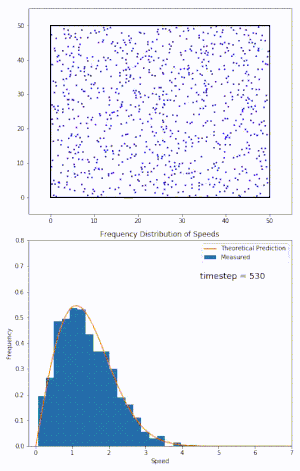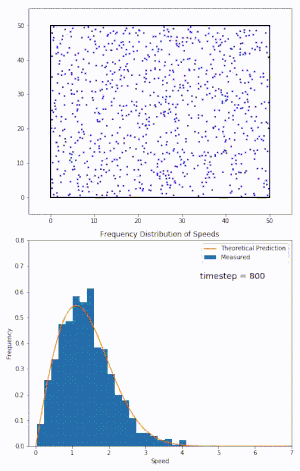
Bataz besteko balioen Darwin-Fowler metodoa erabiliz, Maxwell-Boltzmann banaketa emaitza zehatz gisa eskuratzen da.
Batezbesteko abiadurak.
Maxwell eta Boltzmann-en banaketa funtziotik zenbait parametro estatistiko lor daitezke, probabilitate handiagoko abiadura, batezbesteko abiadura eta batezbesteko abiadura koadratikoa, hain zuzen ere[7].
- Probabilitate handiagoko abiadura, vp, edozein molekulak ( masa berekoak) sisteman izan dezakeen probabilitate handieneko abiadura da eta banaketa funtzioaren maximoak ematen du, zerora berdinduz.
eta, ondorioz,
non, gas idealen konstantea den.
substantzien masa molarra den, ( eta partikulen masa eta Avogadroren zenbakia izanik, hurrenez hurren).
Hortaz, probabilitate handiagoko abiaduraren azken adierazpena hurrengoa izango litzateke:
- Batezbesteko abiadura, abiadura-banaketaren itxaropen matematikoa da.
- Batezbesteko abiadura koadratikoa:
Erreferentziak
- Mandl, F.. (1988). Statistical physics. (2nd ed. argitaraldia) Wiley ISBN 0-471-91533-5. PMC 15487191. (Noiz kontsultatua: 2021-05-04).
- Young, Hugh D.. (2008). Sears and Zemansky's University physics : with modern physics.. (12th ed.. argitaraldia) Pearson Addison Wesley ISBN 0-321-50121-7. PMC 166268535. (Noiz kontsultatua: 2021-05-08).
- Encyclopedia of physics. (Second edition. argitaraldia) VCH Publishers 1991 ISBN 0-89573-752-3. PMC 20853637. (Noiz kontsultatua: 2021-05-08).
- Seshadri, S. R.; Krall, N. A.; Trivelpiece, A. W.; Hirshfield, J. L.. (1974-03-XX). «Fundamentals of Plasma Physics and Principles of Plasma Physics» Physics Today 27 (3): 57–59. doi:. ISSN 0031-9228. (Noiz kontsultatua: 2021-05-08).
- Maxwell, J. C.. (1860-01-XX). «V. Illustrations of the dynamical theory of gases.—Part I. On the motions and collisions of perfectly elastic spheres» The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 19 (124): 19–32. doi:. ISSN 1941-5982. (Noiz kontsultatua: 2021-05-08).
- Müller-Kirsten, H. J. W.. (2013). Basics of statistical physics. (Second edition. argitaraldia) ISBN 978-981-4449-53-3. PMC 822895930. (Noiz kontsultatua: 2021-05-04).
- Serway, Raymond A.. (2012). College physics.. (Ninth edition. argitaraldia) ISBN 978-0-8400-6206-2. PMC 733952215. (Noiz kontsultatua: 2021-05-08).