Koch elur-maluta

Koch elur-maluta, edo Koch izarra, 1904an Helge von Koch matematikariak deskribaturiko irudi itxia da, puntu orotan jarraia baina diferentziagarria ez dena.

Gaur egun fraktal gisa definitzen den kurba mota bat da, prozesu iteratibo baten bidez eraikia dena.

Eraikuntza

Triangelu ekilatero batetik abiatuz, alde bakoitzean beste triangelu ekilatero txikiago bat gehitzen zaio iterazio bakoitzean, sorturiko zuzenki guztiak berdinak izango direlarik. Iterazioa nahi beste aldiz errepika daiteke, infinituraino.

Koch izarraren eraikuntza
1. iterazioa.
2. iterazioa.
3. iterazioa.
4. iterazioa.
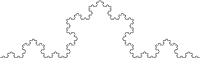5. iterazioa.
6. iterazioa.

Goikoak bezalako hiru kurbak osatzen dute Koch izarra, edo, kanporantz eraiki beharrean barnerantz eraikiz gero, Koch anti-izarra.

Koch anti-izarra (5 iterazio).

Ezaugarriak
Koch izarra irudi fraktala da, zatiki bakoitza osotasunaren isla da.

Prozesua behatuz, ohar daiteke pausu bakoitzean zuzenki baten luzera 4/3 aldiz luzatzen dela. Hasierako hirukiaren luzera 3 unitatekoa suposatuz, n. iterazioan kurba osoaren luzera 3·(4/3)n izango da.

Nabarmentzekoa da infinitu iterazio eginez gero kurbaren luzera infinitua dela, nahiz eta espazio finitu baten barnean gertatu. Hori posible da, Koch elur-malutaren dimentsio fraktala d>1 baita.

Dimentsio fraktalaren kalkulua burutuz gero, d≈1.2618... dela ikusiko da.

Lehenago aipatu bezala, Koch izarra irudi fraktal bat da, alegia, irudiaren zati batek irudi orokorraren itxura berdina du.

Kanpo estekak
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.