Katetoaren teorema

Teorema honen adierazpen matematikoa hurrengoa da:

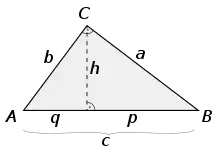
${\displaystyle a^{2}=pc}$ non c hipotenusa den, a eta b katetoak diren eta

${\displaystyle b^{2}=qc}$ p eta q haien proiekzioak c-n, hurrenez hurren.

Beraz, ΔABC triangelu zuzena bi triangelu zuzenetan banatu ahal da, p eta q bakoitzeko kateto bat izanik eta bestea C erpinaren altuera (h). Orduan ΔACH eta ΔBCH triangeluak osatuko dira. Horien angeluak berdinak direnez eta beraz, aldeak proportzionalak, triangeluak antzekoak izango dira.

Antzekoak direla esan daiteke hurrengo arrazoiengatik:

• Hiru triangeluen angeluetako bat angelu zuzena da.
• A eta CBH angelu zorrotzak berdinak izango dira, arku berdinean daudelako eta haien aldeak perpendikularrak direlako, eta berdina gertatzen da B eta CAH angelu zorrotzekin.
• ΔACH eta ΔABC triangeluen arteko antzekotasuna hurrengoa da:

${\displaystyle b/q=c/b}$ → ${\displaystyle b^{2}=cq}$

eta ΔCBH eta ΔABC triangeluen kasuan:

${\displaystyle a/p=c/a}$ → ${\displaystyle a^{2}=cp}$

Edozein triangelu angeluzuzenetan edozein katetoren hipotenusaren gaineko proiekzio ortogonalaren luzera, kateto horren karratuaren eta hipotenusaren luzeraren zatidura da.

Korolario hau katetoaren teorema eta altueraren teorematik ondorioztatzen da. Hasierako bi ekuazioetako batean, p edo q bakantzean lortzen da.

${\displaystyle a^{2}=pc}$ ${\displaystyle q=a^{2}/c}$