Johnson-en solido
Geometrian, Johnsonen solidoak poliedro hertsiki ganbilak dira, bi baldintza hauek betetzen dituztenak: aurpegi guztiak poligono erregularrak dira; eta ez dira uniformeak (hau da, ez dira ez solido platonikoak, ez Arkimedesen solidoak, ez prismak, ezta antiprismak ere). Aurpegi guztiak ez dira zertan izan poligono bera, ezta berdinak diren poligonoak erpin berean elkartu ere; esaterako, alboko aurpegiak triangelu aldeberdinak eta oinarria karratua dituen piramide karratua (J1) Johnsonen solidoetako bat da.
Johnsonen solidoak 92 dira, eta J1, ..., J92 ikurrekin adierazten dira.
1966an, 92 solidoren zerrenda bat argitaratu zuen Norman Johnson-ek, izen eta zenbaki banarekin. Johnsonek ez zuen frogatu 92 baino ez zirela, baina aieruz esan zuen besterik ez zela egongo. Eta 1969an, Viktor A. Zalgaller-ek halaxe frogatu zuen: Johnsonen zerrenda oso-osoa zen.
Johnsonen solidoetako bat, girobikupula karratu elongatua (J37), erpin uniformeak dituen bakarra da: 4 aurpegi erpin bakoitzeko, eta haien kokapena beti da berbera: 3 karratu eta triangelu bat.
Izenak
Johnsonen solido gehienak beste poliedro batzuk erabiliz eraiki daitezke; adibidez, piramide, kupula eta errotondetatik abiatu, eta haiei solido platoniko bat, edo Arkimedesen solido bat, edo prisma bat, edo antiprisma bat lotuta.
Hona hemen Johnsonen solidoen izenetan agertzen diren elementu batzuk:
- Bi- aurrizkiak esan nahi du solido baten bi kopia oinarrietatik lotu direla.
- Elongatu hitzak esan nahi du prisma bat beste solido baten oinarriari lotu zaiola.
- Giroelongatu hitzak esan nahi du antiprisma bat beste solido baten oinarriari lotu zaiola.
- Gehitu hitzak esan nahi du piramide edo kupula bat beste solido baten aurpegi bati lotu zaiola.
- Gutxitu hitzak esan nahi du piramide edo kupula bat beste solido batetik kendu dela.
- Biratu hitzak esan nahi du solido baten kupula bat biratu egin dela, eta beste era batean ahokatu.
Azken hiru eragiketak —gehitzea, gutxitzea, eta biratzea— behin baino gehiagotan egin daitezke solidoa aski handia bada. Hala, bi aldiz egin badugu, bir- aurrizkia gehitzen diogu eragiketaren izenari; esate baterako, solido birbiratu bat da bi kupula biratu dituena. Tri- aurrizkiak adierazten du eragiketa hiru aldiz egin dela; esate baterako, solido trigutxitu bat da hiru piramide edo hiru kupula kendu zaizkiona.
Batzuetan, bi- eta tri- aurrizkiak ez dira aski zehatzak. Solido baten bi aurpegi paralelo ala bi aurpegi zeihar aldatu diren bereiztekotan, para- eta meta- aurrizkiak erabiltzen dira, hurrenez hurren; esaterako, solido parabigehitu bat da bi aurpegi paralelo gehitu zaizkiona; eta solido metabigehitu bat, aldiz, bi aurpegi zeihar gehitu zaizkiona.
Sailkapena
Legenda:
- Jn – Johnsonen solidoaren zenbakia
- Garapena – Irudi laua (zabaldua)
- Erp – Erpin kopurua
- Ertz – Ertz kopurua
- A – Aurpegi kopurua (guztira)
- A3 – 3 aldeko aurpegi kopurua
- A4 – 4 aldeko aurpegi kopurua
- A5 – 5 aldeko aurpegi kopurua
- A6 – 6 aldeko aurpegi kopurua
- A8 – 8 aldeko aurpegi kopurua
- A10 – 10 aldeko aurpegi kopurua
| Jn | Izena | Garapena | Irudia | Erp | Ertz | A | A3 | A4 | A5 | A6 | A8 | A10 | Simetria-taldea |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | piramide karratua |  |
5 | 8 | 5 | 4 | 1 | C4v (*44) | |||||
| 2 | piramide pentagonala |  |
6 | 10 | 6 | 5 | 1 | C5v (*55) | |||||
| 3 | kupula triangeluarra |  |
 |
9 | 15 | 8 | 4 | 3 | 1 | C3v (*33) | |||
| 4 | kupula karratua |  |
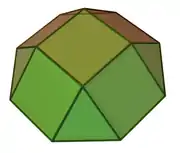 |
12 | 20 | 10 | 4 | 5 | 1 | C4v (*44) | |||
| 5 | kupula pentagonala |  |
 |
15 | 25 | 12 | 5 | 5 | 1 | 1 | C5v (*55) | ||
| 6 | errotonda pentagonala |  |
 |
20 | 35 | 17 | 10 | 6 | 1 | C5v (*55) | |||
| 7 | piramide triangeluar elongatua edo tetraedro elongatua |
 |
 |
7 | 12 | 7 | 4 | 3 | C3v (*33) | ||||
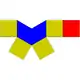
| 8 | piramide karratu elongatua edo kubo gehitua |
 |
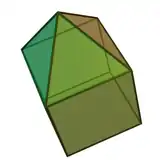 |
9 | 16 | 9 | 4 | 5 | C4v (*44) | ||||
| 9 | piramide pentagonal elongatua | 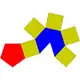 |
 |
11 | 20 | 11 | 5 | 5 | 1 | C5v (*55) | |||
| 10 | piramide karratu giroelongatua | 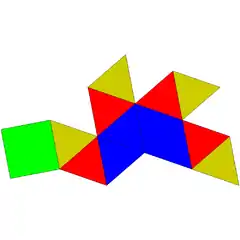 |
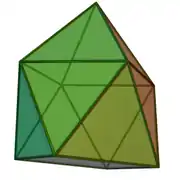 |
9 | 20 | 13 | 12 | 1 | C4v (*44) | ||||
| 11 | piramide pentagonal giroelongatua edo ikosaedro gutxitua |
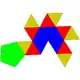 |
 |
11 | 25 | 16 | 15 | 1 | C5v (*55) | ||||
| 12 | bipiramide triangeluarra |  |
 |
5 | 9 | 6 | 6 | D3h (*223) | |||||
| 13 | bipiramide pentagonala |  |
 |
7 | 15 | 10 | 10 | D5h (*225) | |||||
| 14 | bipiramide triangeluar elongatua |  |
 |
8 | 15 | 9 | 6 | 3 | D3h (*223) | ||||
| 15 | bipiramide karratu elongatua edo kubo birgehitua |
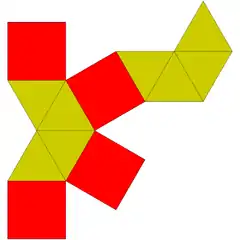 |
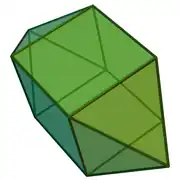 |
10 | 20 | 12 | 8 | 4 | D4h (*224) | ||||
| 16 | bipiramide pentagonal elongatua | 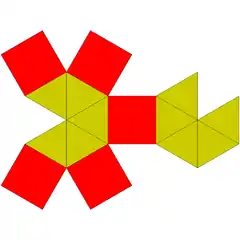 |
 |
12 | 25 | 15 | 10 | 5 | D5h (*225) | ||||
| 17 | bipiramide karratu giroelongatua |  |
 |
10 | 24 | 16 | 16 | D4d (2*4) | |||||
| 18 | kupula triangeluar elongatua | 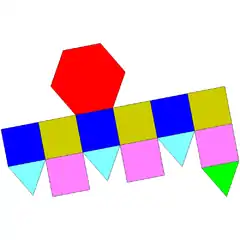 |
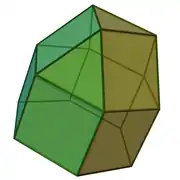 |
15 | 27 | 14 | 4 | 9 | 1 | C3v (*33) | |||
| 19 | kupula karratu elongatua edo erronbikuboktaedro gutxitua |
 |
 |
20 | 36 | 18 | 4 | 13 | 1 | C4v (*44) | |||
| 20 | kupula pentagonal elongatua |  |
 |
25 | 45 | 22 | 5 | 15 | 1 | 1 | C5v (*55) | ||
| 21 | errotonda pentagonal elongatua |  |
 |
30 | 55 | 27 | 10 | 10 | 6 | 1 | C5v (*55) | ||
| 22 | kupula triangeluar giroelongatua | 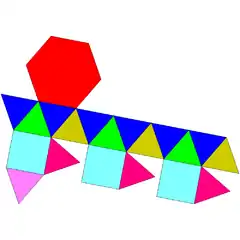 |
 |
15 | 33 | 20 | 16 | 3 | 1 | C3v (*33) | |||
| 23 | kupula karratu giroelongatua | 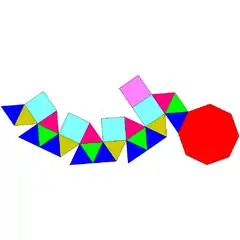 |
 |
20 | 44 | 26 | 20 | 5 | 1 | C4v (*44) | |||
| 24 | kupula pentagonal giroelongatua | 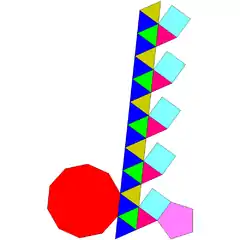 |
 |
25 | 55 | 32 | 25 | 5 | 1 | 1 | C5v (*55) | ||
| 25 | errotonda pentagonal giroelongatua | 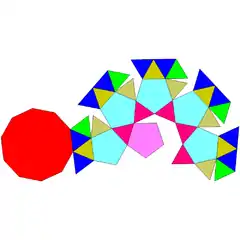 |
 |
30 | 65 | 37 | 30 | 6 | 1 | C5v (*55) | |||
| 26 | girobifastigioa edo girobiprisma triangeluarra |
 |
 |
8 | 14 | 8 | 4 | 4 | D2d (2*2) | ||||
| 27 | ortobikupula triangeluarra edo kuboktaedro biratua |
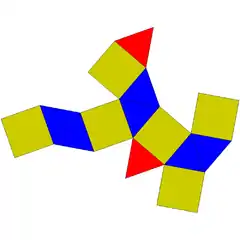 |
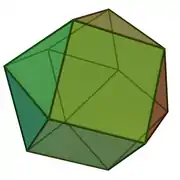 |
12 | 24 | 14 | 8 | 6 | D3h (*223) | ||||
| 28 | ortobikupula karratua | 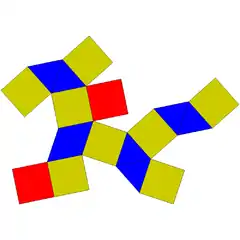 |
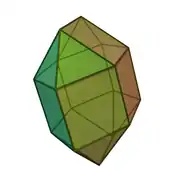 |
16 | 32 | 18 | 8 | 10 | D4h (*224) | ||||
| 29 | girobikupula karratua | 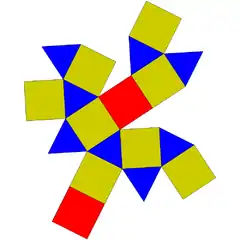 |
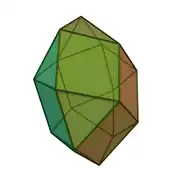 |
16 | 32 | 18 | 8 | 10 | D4d (2*4) | ||||
| 30 | ortobikupula pentagonala | 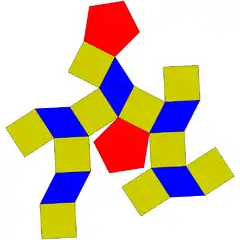 |
20 | 40 | 22 | 10 | 10 | 2 | D5h (*225) | ||||
| 31 | girobikupula pentagonala |  |
20 | 40 | 22 | 10 | 10 | 2 | D5d (2*5) | ||||
| 32 | ortokupularrotonda pentagonala | 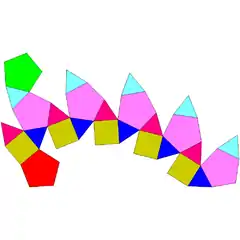 |
 |
25 | 50 | 27 | 15 | 5 | 7 | C5v (*55) | |||
| 33 | girokupularrotonda pentagonala | 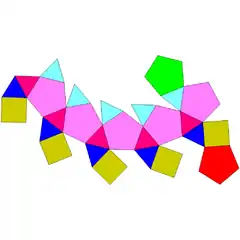 |
 |
25 | 50 | 27 | 15 | 5 | 7 | C5v (*55) | |||
| 34 | ortobirrotonda pentagonala edo ikosidodekaedro biratua |
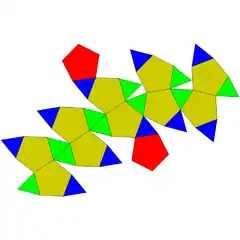 |
 |
30 | 60 | 32 | 20 | 12 | D5h (*225) | ||||
| 35 | ortobikupula triangeluar elongatua |  |
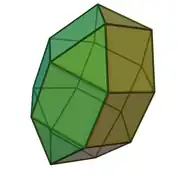 |
18 | 36 | 20 | 8 | 12 | D3h (*223) | ||||
| 36 | girobikupula triangeluar elongatua |  |
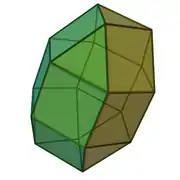 |
18 | 36 | 20 | 8 | 12 | D3d (2*3) | ||||
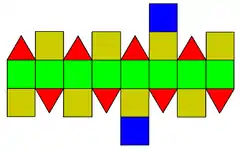
| 37 | girobikupula karratu elongatua edo erronbikuboktaedro biratua |
 |
 |
24 | 48 | 26 | 8 | 18 | D4d (2*4) | ||||
| 38 | ortobikupula pentagonal elongatua |  |
 |
30 | 60 | 32 | 10 | 20 | 2 | D5h (*225) | |||
| 39 | girobikupula pentagonal elongatua | 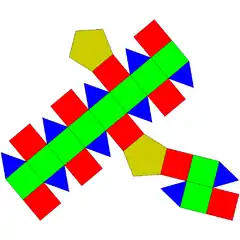 |
 |
30 | 60 | 32 | 10 | 20 | 2 | D5d (2*5) | |||
| 40 | ortokupularrotonda pentagonal elongatua |  |
 |
35 | 70 | 37 | 15 | 15 | 7 | C5v (*55) | |||
| 41 | girokupularrotonda pentagonal elongatua | 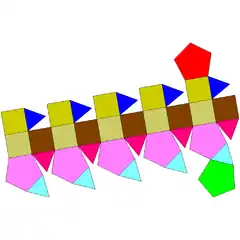 |
 |
35 | 70 | 37 | 15 | 15 | 7 | C5v (*55) | |||
| 42 | ortobirrotonda pentagonal elongatua |  |
 |
40 | 80 | 42 | 20 | 10 | 12 | D5h (*225) | |||
| 43 | girobirrotonda pentagonal elongatua |  |
 |
40 | 80 | 42 | 20 | 10 | 12 | D5d (2*5) | |||
| 44 | bikupula triangeluar giroelongatua (2 forma kiral) |
 |
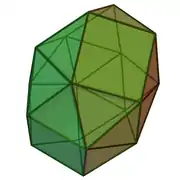 |
18 | 42 | 26 | 20 | 6 | D3 (223) | ||||
| 45 | bikupula karratu giroelongatua (2 forma kiral) |
 |
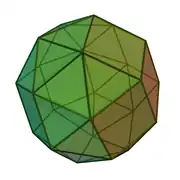 |
24 | 56 | 34 | 24 | 10 | D4 (224) | ||||
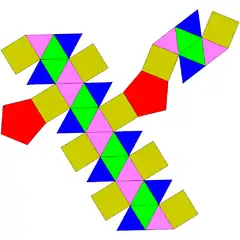
| 46 | bikupula pentagonal giroelongatua (2 forma kiral) |
 |
 |
30 | 70 | 42 | 30 | 10 | 2 | D5 (225) | |||
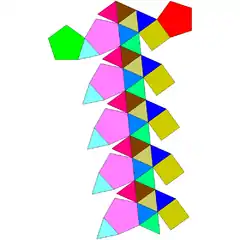
| 47 | kupularrotonda pentagonal giroelongatua (2 forma kiral) |
 |
 |
35 | 80 | 47 | 35 | 5 | 7 | C5 (55) | |||
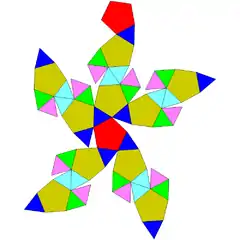
| 48 | birrotonda pentagonal giroelongatua (2 forma kiral) |
 |
 |
40 | 90 | 52 | 40 | 12 | D5 (225) | ||||
| 49 | prisma triangeluar gehitua |  |
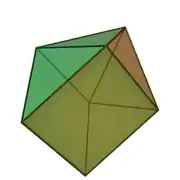 |
7 | 13 | 8 | 6 | 2 | C2v (*22) | ||||
| 50 | prisma triangeluar birgehitua |  |
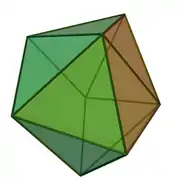 |
8 | 17 | 11 | 10 | 1 | C2v (*22) | ||||
| 51 | prisma triangeluar trigehitua | 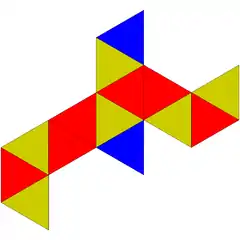 |
 |
9 | 21 | 14 | 14 | D3h (*223) | |||||
| 52 | prisma pentagonal gehitua |  |
 |
11 | 19 | 10 | 4 | 4 | 2 | C2v (*22) | |||
| 53 | prisma pentagonal birgehitua |  |
 |
12 | 23 | 13 | 8 | 3 | 2 | C2v (*22) | |||
| 54 | prisma hexagonal gehitua |  |
 |
13 | 22 | 11 | 4 | 5 | 2 | C2v (*22) | |||
| 55 | prisma hexagonal parabirgehitua | 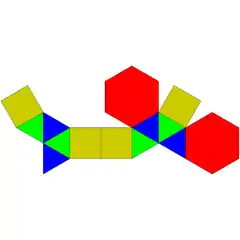 |
 |
14 | 26 | 14 | 8 | 4 | 2 | D2h (*222) | |||
| 56 | prisma hexagonal metabirgehitua |  |
 |
14 | 26 | 14 | 8 | 4 | 2 | C2v (*22) | |||
| 57 | prisma hexagonal trigehitua | 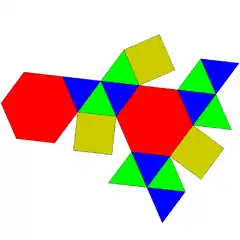 |
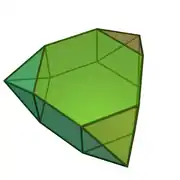 |
15 | 30 | 17 | 12 | 3 | 2 | D3h (*223) | |||
| 58 | dodekaedro gehitua | 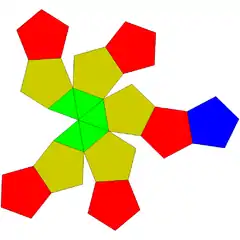 |
 |
21 | 35 | 16 | 5 | 11 | C5v (*55) | ||||
| 59 | dodekaedro parabirgehitua | 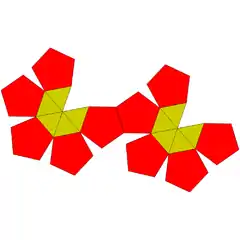 |
 |
22 | 40 | 20 | 10 | 10 | D5d (2*5) | ||||
| 60 | dodekaedro metabirgehitua | 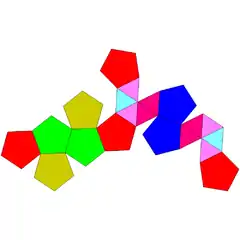 |
 |
22 | 40 | 20 | 10 | 10 | C2v (*22) | ||||
| 61 | dodekaedro trigehitua |  |
 |
23 | 45 | 24 | 15 | 9 | C3v (*33) | ||||
| 62 | ikosaedro metabirgutxitua | 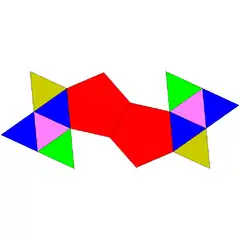 |
 |
10 | 20 | 12 | 10 | 2 | C2v (*22) | ||||
| 63 | ikosaedro trigutxitua | 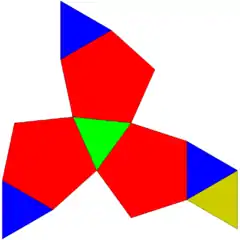 |
 |
9 | 15 | 8 | 5 | 3 | C3v (*33) | ||||
| 64 | ikosaedro trigutxitu gehitua | 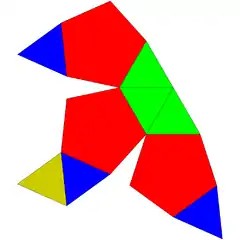 |
 |
10 | 18 | 10 | 7 | 3 | C3v (*33) | ||||
| 65 | tetraedro moztu gehitua |  |
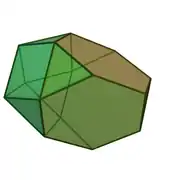 |
15 | 27 | 14 | 8 | 3 | 3 | C3v (*33) | |||
| 66 | kubo moztu gehitua | 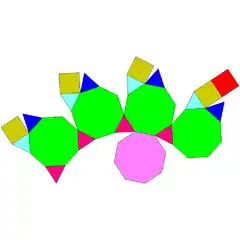 |
 |
28 | 48 | 22 | 12 | 5 | 5 | C4v (*44) | |||
| 67 | kubo moztu birgehitua | 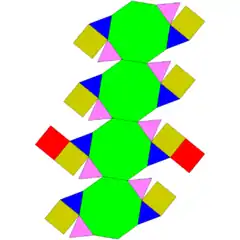 |
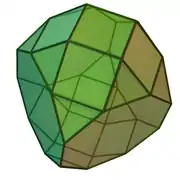 |
32 | 60 | 30 | 16 | 10 | 4 | D4h (*224) | |||
| 68 | dodekaedro moztu gehitua | 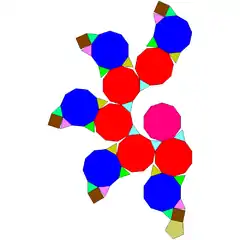 |
 |
65 | 105 | 42 | 25 | 5 | 1 | 11 | C5v (*55) | ||
| 69 | dodekaedro moztu parabirgehitua | 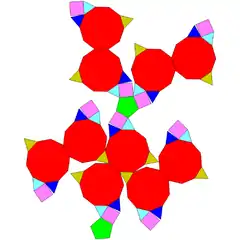 |
 |
70 | 120 | 52 | 30 | 10 | 2 | 10 | D5d (2*5) | ||
| 70 | dodekaedro moztu metabirgehitua | 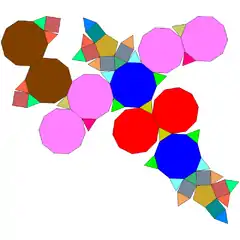 |
 |
70 | 120 | 52 | 30 | 10 | 2 | 10 | C2v (*22) | ||
| 71 | dodekaedro moztu trigehitua | 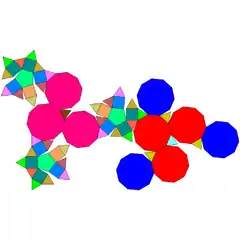 |
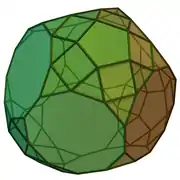 |
75 | 135 | 62 | 35 | 15 | 3 | 9 | C3v (*33) | ||
| 72 | erronbikosidodekaedro biratua | 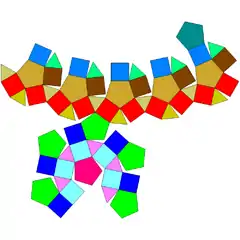 |
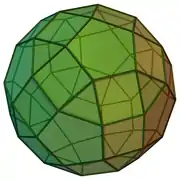 |
60 | 120 | 62 | 20 | 30 | 12 | C5v (*55) | |||
| 73 | erronbikosidodekaedro parabirbiratua | 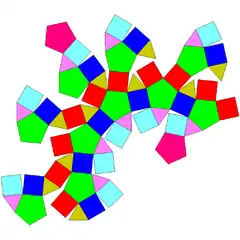 |
 |
60 | 120 | 62 | 20 | 30 | 12 | D5d (2*5) | |||
| 74 | erronbikosidodekaedro metabirbiratua | 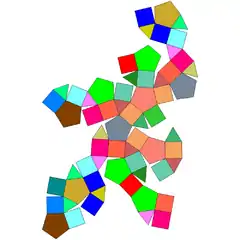 |
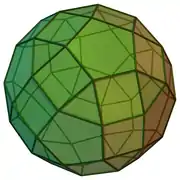 |
60 | 120 | 62 | 20 | 30 | 12 | C2v (*22) | |||
| 75 | erronbikosidodekaedro tribiratua |  |
 |
60 | 120 | 62 | 20 | 30 | 12 | C3v (*33) | |||
| 76 | erronbikosidodekaedro gutxitua |  |
 |
55 | 105 | 52 | 15 | 25 | 11 | 1 | C5v (*55) | ||
| 77 | erronbikosidodekaedro gutxitu parabiratua |  |
 |
55 | 105 | 52 | 15 | 25 | 11 | 1 | C5v (*55) | ||
| 78 | erronbikosidodekaedro gutxitu metabiratua |  |
 |
55 | 105 | 52 | 15 | 25 | 11 | 1 | Cs (*11) | ||
| 79 | erronbikosidodekaedro gutxitu birbiratua |  |
 |
55 | 105 | 52 | 15 | 25 | 11 | 1 | Cs (*11) | ||
| 80 | erronbikosidodekaedro parabirgutxitua |  |
 |
50 | 90 | 42 | 10 | 20 | 10 | 2 | D5d (2*5) | ||
| 81 | erronbikosidodekaedro metabirgutxitua | 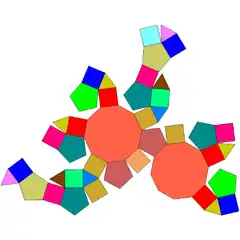 |
 |
50 | 90 | 42 | 10 | 20 | 10 | 2 | C2v (*22) | ||
| 82 | erronbikosidodekaedro birgutxitu biratua |  |
 |
50 | 90 | 42 | 10 | 20 | 10 | 2 | Cs (*11) | ||
| 83 | erronbikosidodekaedro trigutxitua |  |
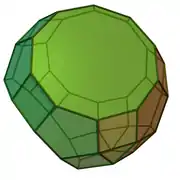 |
45 | 75 | 32 | 5 | 15 | 9 | 3 | C3v (*33) | ||
| 84 | biesfenoide kamutsa edo dodekaedro siamdarra |
 |
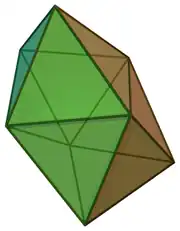 |
8 | 18 | 12 | 12 | D2d (2*2) | |||||
| 85 | antiprisma karratu kamutsa |  |
 |
16 | 40 | 26 | 24 | 2 | D4d (2*4) | ||||
| 86 | esfenokoroa | 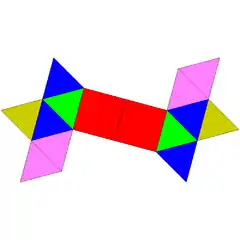 |
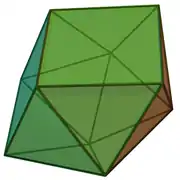 |
10 | 22 | 14 | 12 | 2 | C2v (*22) | ||||
| 87 | esfenokoroa gehitua | 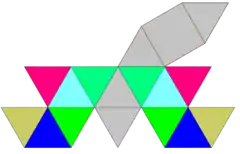 |
 |
11 | 26 | 17 | 16 | 1 | Cs (*11) | ||||
| 88 | esfenomegakoroa | 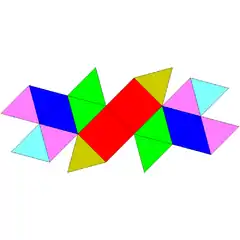 |
 |
12 | 28 | 18 | 16 | 2 | C2v (*22) | ||||
| 89 | Hebesfenomegakoroa |  |
 |
14 | 33 | 21 | 18 | 3 | C2v (*22) | ||||
| 90 | biesfenozingulua | 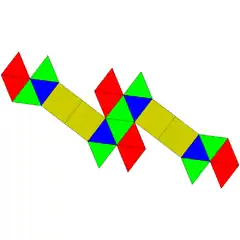 |
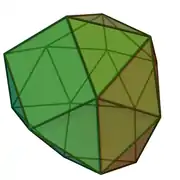 |
16 | 38 | 24 | 20 | 4 | D2d (2*2) | ||||
| 91 | Bilunabirrotonda | 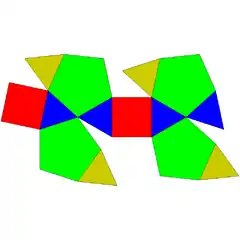 |
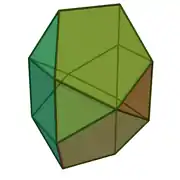 |
14 | 26 | 14 | 8 | 2 | 4 | D2h (*222) | |||
| 92 | hebesfenorrotonda triangeluarra |  |
 |
18 | 36 | 20 | 13 | 3 | 3 | 1 | C3v (*33) |
Erreferentziak
- Norman Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, or. 169–200. 92 solidoen jatorrizko izenak, eta besterik ez dagoelako aierua.
- Viktor A. Zalgaller. (1969). Consultants Bureau ed. Convex Polyhedra with Regular Faces. No ISBN. Johnsonen solidoak 92 baino gehiago ez daudelako lehenengo froga.
Ikus, gainera
- Ia Johnsonen solidoak
- Catalanen solidoak
- Poliedro toroidala
Kanpo estekak
- (Ingelesez) Weisstein, Eric W.: "Johnson-en solido" MathWorld-en.