Jatorrizko funtzio
Matematikan, [a,b] tarte itxi batean definituriko f(x) edozein funtzio erreal emanda, f(x) funtzioaren jatorrizkoa edo antideribatua, [a,b] tartean definitua eta deribagarria den F(x) beste funtzio bati esaten zaio, non tarte horretan F(x) funtzioaren deribatua f(x) funtzioa den. Hau da:
f funtzio batek tarte batean jatorrizkorik izateko baldintza nahikoa jarraitua izatea da.
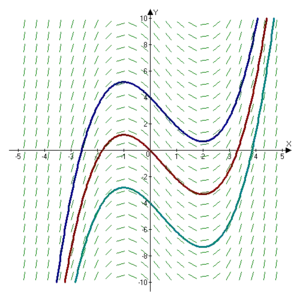
Beraz, f funtzio batek jatorrizkorik badauka tarte batean, ezin konta ahala jatorrizko funtzio izango ditu, haien artean desberdinak konstante batengatik baino ez direnak: F1 eta F2 f-ren jatorrizkoetariko bi funtzio badira, orduan existitzen da K zenbaki erreala, integrazio-konstantea deritzoguna, non F1 = F2 + K den. Horregatik, f funtzioaren jatorrizkoen multzoa F + K da. Multzo horri f-ren integral mugagabea deritzogu eta honela adierazten dugu:
- edo
Funtzio baten jatorrizkoa kalkulatzeko prozesuri integrazio mugagabea deritzogu eta deribazioaren alderantzizko prozesua da. Integral mugagabeak integral mugatuekin erlazionatuta daude kalkuluaren oinarrizko teoremaren bitartez, eta hamaika funtzioren integral mugatua kalkulatzeko metodoa ematen dute.
Jatorrizkoen taulak
Funtzio sinpleak
konstante errealak dira, izanda eta integrazio-konstantea.
| bada; bestela | ||
Kontuan izan taula horrek funtzioaren jatorrizkoak dituela (zenbaki arrunta) zenbakietarako ez ezik, baita (zenbaki osoa) zenbakietarako ere, polinomioekin lan egitea errazten duena; esaterako: , eta zenbaki erreal ez osoa den kasuan ere, adibidez , .