Isurpen-limite

Isurpen-limitea edo limite elastikoa materialen zientzian erabiltzen den terminoa da, eta material batek, deformazio plastikorik edo iraunkorrik gabe, jasan dezakeen tentsio maximoa adierazten du. Balio hori tentsio-deformazio kurba batean islatzen da (1. irudian ikus daiteke tentsio-deformazio kurbaren adibide bat). Balio horretara iritsi baino lehen deformazioak elastikoak izaten dira soilik, materiala bere hasierako formara bueltatzen delako tentsioa kendutakoan. [1]

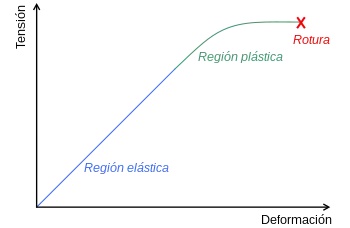
[1] irudia: tentsio-deformazio kurba, bi zonaldeak banatuta: eremu lineala edo elastikoa eta eremu ez-lineala edo plastikoa. Azken puntua haustura-limitea izaten da.

Material guztiek duten propietate bat da, eta horien gogortasuna determinatzeko erabiltzen da. Gainera, hutsegite-teoriak lantzean ezinbestekoa da isurpen-mugaren balioa, horrekin material edo pieza baten deformazioak azter daitezkeelako.

Bere balioa jakiteko hainbat proba egin daitezke, horretarako makina desberdinak erabiliz. Hauen artean trakzio-saiakuntza dugu, eta proba horretan pieza angeluzuzen bati indar bat aplikatzen zaio alde luzearekiko edo motzarekiko ─nahi den aplikazioaren arabera─, pieza apurtu arte.

Hooke-n legea

Hooke-ren legea edo Hooke-ren elastikotasun-legea soilik aplika daiteke eremu linealean ─deformazioak iraunkorrak ez diren eremua─, eta honako hau baieztatzen du:

“Trakzio-saiakuntza batean material elastiko batek jasaten duen deformazioa aplikatutako indarrarekiko zuzenki proportzionala da, eta bere sekzio transbertsalarekiko alderantziz proportzionala.” [2]

[2] irudia: trakzio- eta konprezio-saiakuntzetan probetak jasango duen indarraren norabidea eta noranzkoa.

Beraz, honako formula hau aplika daiteke lehen aipatutako zonaldean, Poisson-en koefizientearen alderantzizko formula izanda:


·: luzapena

·: hasierako luzera

·: aplikatutako indarra

·: Young-en modulua

·: piezaren sekzio transbertsala (aplikatutako indarraren ardatzarekiko perpendikularra den probetaren sekzioa)

Hooke-n legearen bidez isurpen-limitearen aurreko luzapen guztiak lor daitezke, isurpen-limitea lege horren limite baliogarria izanda.

Material desberdinen isurpen-limitea

Hona hemen material desberdinen isurpen-muga edo isurpen-tentsioa, eta haustura-tentsioa batzen dituen taula, balioak nahiko orokorrak izanda: [3]

Materiala Isurpen-limitea (MPa) Haustura-tentsioa (MPa)
Eztainua 9 - 14 50 - 200
Nikela 14 - 60 140 - 195
Aluminioa 15 - 20 40 - 50
Burdina 80 - 100 350
Kobrea 100 - 200 210
Titanioa 100 - 225 240 - 370
Tantaloa 180 200
Tungstenoa 550 560 - 620

Neurketa-metodoak

Neurketa-metodorik erabiliena ordenagailu bidezko trakzio-saiakuntza bidez egiten da, eta hortik ateratzen diren datuak grafikatzen dira tentsio-deformazio kurba lortzeko. Horrela, material bakoitzak kurba desberdin bat izango du.

Trakzio-saiakuntza
[3] irudia: probeta normalizatu bat eta bere kokapena trakzio-saiakuntza egiteko.

Material zehatz batez egindako probeta normalizatu bat hartzen da (3. irudian ikus daiteke adibide bat) eta apurketa gertatu arte handituz doan esfortzu axial baten menpe jartzen da. Apurketa gertatu baino lehen, tentsio zehatz batetik aurrera, isurpen-limitea, deformatzen hasiko da tentsioa handitu ahala, deformazio hori tentsioaren norabidearekiko paraleloa izanda. Saiakuntza horren bitartez materialak indar estatiko baten eraginpean duen erresistentzia neurtzen da. Saiakuntza amaituko da probeta guztiz apurtzen denean; hau da, materialaren haustura-tentsiora ailegatutakoan. [4]

Ordenagailu batean instalatuta dagoen software edo programa informatiko baten bidez, saiakuntzan lortzen diren tentsio eta deformazio datu guztiak tentsio-deformazio kurban islatzen dira. Ondoren, kalkulu matematikoak erabiliz, materialaren ezaugarri mekanikoak lor daitezke. Hauek dira lortzen diren ezaugarri nagusiak:

  • Young-en modulua: material elastiko baten portaera zehazten duen parametroa, aplikatutako indarraren norabidearen araberakoa. Hooke-ren legearen alderantzizkoa da. [5]
  • Poisson-en koefizientea: indarraren norabidean, luzetarako luzamenduaren eta luzetarako konpresio transbertsalaren arteko erlazioa.
  • Proportzionaltasun-limitea: luzapena kargarekiko proportzionala da balio honetatik behera.
  • Isurpen-limitea edo limite-elastikoa: probetak jasan dezakeen tentsio maximoa isurpena baino lehen.
  • Haustura-tentsioa: probetak jasan dezakeen tentsio maximoa apurketa baino lehen.
  • Haustura-luzapena: probeta apurtzean duen luzapen edo elongazio maximoa.
  • Kalibratutako luzera: bai deformazio unitarioa edo luzera-aldaketa bai luzapena determinatzeko erabiltzen den probetaren zati baten luzera.
  • Azaleraren murriztea eta estrikzioa: zeharkako sekzioaren azaleraren murriztea.

Erreferentziak
  1. (Ingelesez) Yield (engineering). 2020-10-18 (Noiz kontsultatua: 2020-11-07).
  2. (Gaztelaniaz) Ley de elasticidad de Hooke. 2020-10-14 (Noiz kontsultatua: 2020-11-07).
  3. «Yield Strength - Strength ( Mechanics ) of Materials - Engineers Edge» www.engineersedge.com (Noiz kontsultatua: 2020-11-07).
  4. Trakzio-saiakuntza. 2020-10-06 (Noiz kontsultatua: 2020-11-07).
  5. (Gaztelaniaz) Módulo de Young. 2020-10-30 (Noiz kontsultatua: 2020-11-07).

Ikus, gainera

Kanpo estekak
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.