Isaac Newton
Isaac Newton (Woolsthorpe-by-Colsterworth, Lincolnshire, Ingalaterra, 1643ko urtarrilaren 4agreg./1642ko abenduaren 25jul. - Kensington, Londres, 1727ko martxoaren 31greg./1726ko martxoaren 20jul.) zientzialaria, alkimista, filosofoa eta matematikaria izan zen.
| Artikulu sorta honen partea: |
| Mekanika klasikoa |
|---|
Munduko zientzialari hobenetarikotzat jotzen dugu gaur egun. Kalkuluaren sortzailea, Grabitatearen Legearen aurkitzailea, eta mekanika klasikoko legeen asmatzailea da. Argia eta optika aztertu zituen (hala ere, bera modu matematikoan egin zuen azterketa).
Bere ikerketa zientifikoetako emaitza garrantzitsuenak hauek dira:
- Argia prisma batetik pasatzean sortzen den kolore espektroa argiarena bera dela frogatzea, eta ez prismarena (Roger Baconek XIII. mendean esan bezala).
- Argia partikulez osatua egon zitekeela argudiatu
- Eroankortasun termikoaren lege bat sortu
- Soinuaren abiadura airean jorratu
- Izarren sorreraren inguruko teoria bat sortu
- Grabitatearen Legea sortu
Gottfried Leibnizekin batera kalkulu integral eta diferentziala sortu zuen. Binomioen teorema sortu zuen. Joseph-Louis Lagrangek esan zuen: "Newton inoiz egon den jeinurik handiena da, eta baita zorte handiena izan duena ere, behin baino ezin delako aurkitu sistema bat mundu osoa arautzen duena".
Zientzia arloko beste aurkikuntzen artean kolore espektroa dago, ikus dezakegula hemen argi zuri bat prisma baten barrutik pasatzen denean (Roger Bacon esan zuen bezala XIII. mendean); honek esaten du argia partikulekin sortuta dagoela eta konbektzio termiko batengatik airean dauden objektuen hozpen tasa deskribatzen du. Hortik kanpo, soinuaren abiadura bilatu zuen eta izarren jatorria aurkitu zuen. Fluxuen mekanikaren lehen deskribatzailea izan zen, biskositatearen lege bat eginez.
Bizitza
Isaac Newton 1643ko urtarrilaren 4an jaio zen. Hain goiztiar eta txiker jaio zenez, ez zuten uste astebete baino gehiago biziko zenik. Bere bataioa urtarrilaren 12an izan zen.
Bere gurasoak nekazariak ziren, Isaac Newton eta Hannah Ayscough ziren. Ez zuen ezagutu bere aita, bera jaio baino lehen hil zelako. Bere ama, beste gizon batekin ezkondu zen, Barnabás Smith. Honek ez zuen berea ez zen haur batekin bizi. Hori dela eta, Isaac, bere amonarekin bizi izan zuen, Barnabás hil arte.
Hannah-en senarra hil zenean, 1653. urtean, Isaac bizi zen etxera bueltatu zen, bi haur berriekin, baina lotura hori oso motza izan zen 12 urterekin “The King’s School”-era bidali zutelako ikastera. Bertan ikasi zituen hizkuntzak Latina eta Greziera klasikoa ziren, eta Aritmetikako eta Geometriazko oinarriak ikasi zituen. Ikasgai horiek, lehen hezkuntzazko eskola guztietan ikasten zen. Bestalde, bere irakaslea entzute handia zuen, Stokes jauna.
Newtonen lehen hezkuntzak oso erabilgarria izan zen berarentzat. Matematikako eta filosofiako lanak Latinez idatzi zituen, garai hartan erabiltzen zen hizkuntza[1]. Ikasketa hauei esker, Europar zientzialariekin harremanetan jarri zen. Garai horretan Bibliaren ikasketak oso garrantzitsuak ziren, eta ikasketa programa jarraitzeko eta Ingalaterrazko Fede Protestantea bermatzeko, Latinez irakurtzen zen. Isaac-en kasuan, aukera handiak izan zituen Teologiako ikasketak egiteko, bere aitaordeak beraren teologiako liburu guztiak eman baitzizkion Newton-i.
Grantham herrian bizi izan zenean, Clark jaunaren etxean bizi zen, High Street kalean. Hiru umeekin bizi izan behar zuen, Edward, Arthur eta neska bat. Fisikariaren haurtzaroarengatik, oso zaila izan zuen bere adina zuten beste umeekin harremanak izatea. Bere aitonekin bizi izan zuenez, isolamendu egoeran hazi zen. Bere adinekoak inbidia handia zuen, ikusten zutelako Isaac haiek baino azkarra zelako, eta berak adimenaz baliatu zen besteei bihurrikeriak egiteko. Bere lagun batek, William Stukeley, Newtoni buruzko informazioa biltzen hasi zen Grantham-ko etxean bizi zenean. Lagun honek Newtonen arazoari erantzun bat aurkitu zion. Uste zuen Newtonek lagunak egiteko aukera gutxiago izan zituela besteak baino askoz azkarragoa zelako. Hori dela eta, besteak Newton onartzen ez zutelako, Newton besteak gaizki tratatzen eta gaiztakeriak egiten hasi zen.
Catherine Storeri, bere laguna , egurrezko altzari bat egin zuen bere panpinentzat. Gertaera hauei esker, esan omen da, handiagoak izan zirenean erromantze bat izan zutela bi gazteek. Hori suposatzen du, Storer, Isaac-en lehenengo eta azken neska-laguna. Geroago, neska hau Vincent abizena zuen jaun batekin ezkondu zen.
Stukeley-en idatzietan, Isaac jenio bat bezala. Kapazitate handia zuen lan mekanikoentzat eta asmakizun arraroak sortu zituen bere amak ematen zion diruarekin. Egurrezko objektuak, panpinen altzairuak eta maketak ziren bere lanik gogokoenak eta hoberenak. Orobat, haize errota baten maketa bat sortzea egurrarekin. Newtonen kopia, bestea baino hobea zen, eta bere etxeko teilatuaren gainean jarri zuen. Honen eredua noria bat zuen, errotaria deitzen zena.
Beste asmakizun nabarmen bat lau gurpilezko orga izan zen. Honi indarra emateko barruan biradera bat erabiltzen zen. Beste bat, paperezko esku-argi bat izan zen, eskolara iristeko egun ilunetan. Linterna hau erabiltzen zuen kometa bati lotuta bizilagunak beldurtzeko ere. Asmakizun hauek sortzeko, denbora behar zuen eta hori lortzeko, eskolako lanak ez zituen egiten, eta bere kalifikazioak eta postua galtzen zuenean, ikasten hasten zen berriro. Sortzen zituen gauzen ideiak, The Mysteries of Nature and Art liburutik ateratzen zituen. Bertatik ateratzen zituen gaitasunak marrazketakoak, kolorezko tinteak sortzen edo txorien harrapaketari buruz, besteen artean. Haizezko errota ere liburu honetan oinarritu zen.
Isaac Newton, besteen laguntasuna lortzekotan, bere klasekideei oparitzen zien paperezko linternak, baina ez zuen lortu, prozedura hauekin erakusten zuen bakarra besteak baino azkarragoa zela demostratzen zuelako.
Berarentzat erlojuak denbora-pasa garrantzitsu bat izan ziren bere herrian. Colserworth-eko elizan bederatzi urterekin sortutako bat dauka. Hauek erronka handi bat ziren erreminten erabilpenarekin. Clark-en etxea erlojuz bete zuen; bere logela, etxeko logelak, sarrera… Bestela esanda, etxean eguzkia sartzen den edozein gelan. Paretetan puntak iltzatu zituen orduak, erdiak eta laurdenak neurtzeko, eta kordak gurpilei lotu zituen itzalak neurtzeko hurreneko egunetan.
Unibertsitatea
Hemezortzi urterekin Cambridgeko unibertsitatean sartzea lortu zuen bere ikasketak jarraitzeko. Hala ere, ez zen beti klasera joaten, bere pasioa eta interesa liburutegia zelako. Trinity College-an graduatu zen, bereziki autodidakta izanez. Hori lortzeko garai hartako Matematikako eta Filosofiako liburuak irakurtzen zituen. 1663an Clavis mathematicae (William Oughtred), Geometría (Descartes), Astronomiae Pars Optica (Kepler), Opera mathematica (Viète), eta Aritmetica (John Wallis) liburuak irakurri zituen; irakurketa hauengatik baliatu zen bere ikerketak jarraitzeko, adibidez, serie infinituak, binomioaren teorema eta zenbait koadratura.
Beste zientzialariekin egindako lanak
1663. urtean Isaac Barrow ezagutu zuen eta bere matematikako irakaslea izan zen. Garai horretan Galileo, Fermat, Huygens, Descartes eta beste batzuen lanak berregiten hasi zen. Azkar Barrow aurreratu zuen, eta azkenean Barrow Newtoni laguntza eskatzen zion matematikako problemekin laguntzeko.
Urte haietan, geometria eta optika paper garrantzitsu bat zuten Isaac-en bizitzan. Ildo beran, bere fama handitu zen Royal Society-arekin harremanak hasi zituelako. Berak bere asmakizunak eta teleskopio bat bidali zien eta taldekideetan grina hasi zen bere lanarekin, baina baita batzuen inbidia hasi zen, Robert Hooke adibidez. Hori izan zen hasiera beste zientzialarien kontrako gatazkak. Beti esan da jarrera agresiboa zuela besteen kontra. Royal Society-eko buru bezala, diktadore krudel eta mendekari bat izan zen.
Mekanika eta grabitateari buruzko lanak hasi baino lehen, Hooke-en gutun bat jaso zuen non honek idazten zion bere ideia intuitiboak grabitateari buruzkoak. Newton problemari erantzun bat aurkitu zion, Robert Hooke lortu ez zuena. Erantzun guzti horiek esaten den munduko libururik honenean idatzi zuen: “Philosophiae naturalis principia mathematica”.
1693. urtean krisialdi psikiko bat izan zuen, sortuta isolamendu urteengatik. Denbora horretan ez zuen ezta jaten edo lo egiten. Depresio eta paranoia izan zuen. Gutunen bidez bere lagun batekin hitz egiten zuen, John Lockerekin. Berari aipatzen zion nola zegoen, eta batzuetan egin ez zuen gauzengatik errudun sentitzen zen. Historialari batzuek esaten zuten krisialdi hori sortu zela erlazioa izaten bukatu zuen bere ikasle batekin, Nicolás Fatio de Duillier. Beste batzuek esaten zuen bere gaixotasunak Merkurioa sortu zuela, alkimiako esperimentuen ondorioz.

Beste interes batzuk, alkimia eta erlijioa ziren. Gainera, gai hauetako idazmenak askoz gehiago ziren zientziari buruzkoak baino. Erlijioko idazlanak gatazka handiak sortu zizkion Trinity College-rekin. Izan ere, unibertsitatearen kontrako idazlanak egin zituen eta unibertsitateko kidea zen.
Lehenengo lanak
1664. urtetik hasi zen lanean bereziki matematikako zenbait problemetan. Lehenengoa, binomioaren teorema izan zen, eta John Wallis-en lanei esker modu berri bat sortu zuen Fuxionen kalkulua deitzen zena. Geroago, familiaren baserrira bueltatu izan behar zuen epidemia larri batengatik.
Bere etxean eta familiarekin bi urtez egon zen; hala ere, asko aprobetxatu zuen denbora hori non ikerketa asko egin zituen, eta, besteen artean, grabitazio unibertsalaren legea sortu zuen, mekanika klasikoari sarrera eman zion, aurretik aipatutako fluxioen metodoa sortu eta koloreen natura fisikoa aztertu zuen. Bestalde, aurkikuntza hauek denbora askoz ez zion inori esan, kritikak eta ideien lapurretak saihesteko. 1667. urtean, Cambridgeko unibertsitatera bueltatu eta ikasketak jarraitu zituen.
Kalkuluaren garapena
1667. urtetik 1670.-era optikari buruzko ikerketak hasi zituen; hori dela eta, Trinity College-ko fellow aukeratu zuten. 1669an, haren irakaslea Isaac Barrow, matematikako “Catedra Lucasiana”-ri uko egin zion, Newton bere oinordekoa izan zelako 1696. urtera arte. Urte berdinean John Collinsi, Barrow-en bidez, Analysis per aequationes número terminorum infinitos bidali zion. Newtonentzat idatzi hau sarrera izan zen sistema orokor batentzat geroago jarraituko zuena: kalkulu diferentzial eta integrala.
Newton aurkitu zituen kalkulu diferentzial eta integralaren oinarriak 1665 eta 1666. Urteen artean eta hurrengo hamarkadan gutxienez hiru ikuspuntu egin zituen bere analisi berriari buruz.
Newton eta Leibniz eztabaida bat izan zuten, ez zutelako adosten nork sortu zuen matematikako adar hau. Historialariak esaten zuten biak ondo garatu zutela kalkulua, bakoitzak bere kabuz; esaten da Leibnizen notazioa hobea zela eta Newtonen formulazioa ere. Hala ere, Newtonena problema praktikoei hobe aplikatzen zen. Polemika hau Ingalaterrako eta Europako matematikariak zatitu zuen, baina zatiketa hau ez zen izan hain garrantzitsua bi matematikari hauek elkar lan egiteari uko egiteko.

Isaac Newtonen lana geometria analitikoarekin garatu zuen, deribatuei ikuspuntu geometriko eta analitikoa aplikatuz. Newtonek ere bilatzen zuen nola koadratu zenbait kurba eta koadraturen eta tangentzien erlazioa bilatuz. Roberval-en ikasketen ondorioz, Newtonek konturatu zen tangentzien metodoa erabil zezakeela ibilbide ezagun baten aldiuneko abiadura jakiteko. Bere lehenengo ikerketetan Newtonek bakarrik lan egiten du lan geometrikoekin, adibidez, nola aurkitu tangentzia, kurba eta azalera Deskartesen geometria analitikoan oinarrituz. Hala eta guztiz ere, Deskartesen teoria hobetzeko, ekuazio eta aldagaiekin lan egiten hasi zen, sistema kartesiarra deuseztatuz.
1666. urtean, matematikei uko egin zien, eta naturazko ikasketak hasi zituen Principia sortuz.
Newton-Cotes formulak
Formula hauek Isaac Newton eta Roger Cotes idatzi zituzten eta zenbaki analisiaren arloan daude. Zenbaki integrazioaren formulak dira eta interpolatorio motakoak dira non distantzia berdineko arteko puntuen arteko funtzioa ebaluatzen da, integralaren inguruko balore bat lortzeko. Funtzio hau tarte gehiago lortzen dituen heinean, prezisio gehiago izango du erantzunak.
Metodo hau eragina gehiago izango du funtzioen puntuak hobe ezagutzen badira. Puntu hauek aldatzen baditugu eta ebaluatu dugun funtzioa beste modu batzuekin aurkitzen badugu, Gaussen kuadratura bezala, eraginkorragoa izango da.
Sarrera
zenbaki integrala egiteko, Newton-Cotes formulak erabiliz, [a,b] tartea zatitu behar da n tarte berdinetan. Horrela n+1 puntuak lortuko dira non funtzio hau ebaluatzen da:
a=x0 eta b=xn Newton-Cotes-eko formula itxiak dira, tarteen muturrak integralean daudelako, bain aez baldin badira kontuan hartzen, Newton-Cotes-eko formula irekiak izango dira. Kalkulatzeko, hurrengo funtzioa erabiliko dugu:
non:
Langrage-ren polinomioa da non esan dezakegu
Eta funtzio hau forma honekin adierazten da:
Non wi pisuak honekin definituak daude:
Newton-Cotes-en formula itxiak
Hauek Newton-Cotes-en formula itxi batzuk dira:
fi notazioa, f(xi)-ren laburpen bat da, non:
Eta n maila izango da.
Trapezioaren erregela
Trapezioaren erregelarekin funtzio baten integrala lortu nahi da lehen mailako polinomio batekin, hau da, aztertu nahi den funtzioaren puntu guztiak zuzen baten bidez lotuz.
Eta hau, errorea da:
Non a eta b arteko zenbaki bat da.
Simpson-en erregela
Simpsonen erregela (Thomas Simpson-ek izendatu zuena) funtzio baten inguruko integral bat aurkitzen du bigarren edo hirugarren mailako polinomio bat erabiliz. link=https://es.wikipedia.org/wiki/Archivo:Integration_simpson.svg|eskuinera|Simpson-en erregelaren irudikapena
Simpson-en erregela 1/3
Simpsonen erregela hau erabiltzen du ondoz ondoko hiru puntu non bigarren mailako polinomio bat erabiliz funtzio bat aztertzen du.
Eta errorea hau da:
Non a eta b arteko zenbaki bat da.
Simpson-en erregela 3/8
Erregela hau erabiltzen ditu ondoz ondoko lau puntu non hirugarren mailako polinomio batekin funtzioa aztertuko du.
Eta errorea hau da:
Non a eta b arteko zenbaki bat da.
Boole-ren erregela
Boole-ren erregela (George Boole sortu zuena) ondoz ondoko bost puntu erabiltzen ditu, bata bestearen artean distantzia berdina dutena, funtzio baten inguruko integral bat erabiltzen duena laugarren mailako polinomio bat erabiliz.
Eta errorea hau da:
Non a eta b arteko zenbaki bat da.
Bosgarren mailako erregela
Erregela hau ondoz ondoko sei puntu distantziakide erabiltzen ditu funtzio baten integrala kalkulatzen du bosgarren mailako polinomio bat erabiliz.
Seigarren mailako erregela
Erregela hau ondoz ondoko zazpi puntu distantziakide erabiltzen ditu funtzio baten integrala kalkulatzen du seigarren mailako polinomio bat erabiliz.
Newton-Cotes-en formula irekiak
Hauek dira Newton-Cotes-en formula ireki batzuk:
Puntu erdiko erregela. Riemann-en integrala
Sistema hau funtzioa laukizuzenetan zatitu du eta puntu erdiko balorearen altuera berdina izan behar du. Horrela, inguruko integral bat kalkulatuko da zero mailako polinomio baten bidez.
Eta errorea hau da:
Non a eta b arteko zenbaki bat da.
Erregela konposatuak
Newton-Cotes-en formulen zehaztasuna handiagoa izango da, zatitu duzun funtzioa tarte gehiagorekin kalkulatzen badituzu, hau da, tarte txikiagoetan zatitzen baduzu. [a,b] tartea orokorrean handiagoa izango da, horrela tarte hauek txikiagotzen ditugu Newton-Cotes-en formulak erabiliz. Erregela hauek erregela konposatuak dira.
Trapezioaren erregela konposatua
Hau, erregela konposatuaren eredu bat da.
Non azpitarteak dira
eta
azpitarteen arteko distantzia da.
Argiari buruzko lanak
1670 eta 1672 urteen artean oso gogor lan egin zuen optikari eta naturaren argiari buruz. Ondorioztatu zuen argi zuria kolore banda batekin osatuta zegoela (gorria, laranja, horia, berdea, zian, urdina eta morea), bana daitezkeela prisma bat erabiliz. Lan honetatik, ondorio batera iritsi zen eta esan zuen edozein teleskopio errefraktorea aberrazio bat jasan izango zuela, gaur hobeto ezaguna aberrazio kromatikoa izenarekin; aberrazio honetan argi bat kolore guztietan sakabanatzen dira leiar bat zeharkatzean. Arazo hori saihesteko teleskopio islatzaile bat asmatu zuen, Newtonen teleskopioa deitzen dena. Argiari buruzko ikerketen ondorioz teoria orokorra formulatu zuen, non esaten du argia korpuskuluekin osatuta dagoela eta lerro zuzenean bidaiatzen duela, ez uhinen bidez. Garai hartan argitaratutako liburua, zientzialariek kritikatu zuten; haien artean, Robert Hooke eta Huygens. Hauek esaten zuten argia uhinen bidez garraiatzen zela, aurretik esaten zen bezala. Hori dela eta, bere burua isolatu zuen ikasten eta ikertzen Cambridgeko estudio batean.
1704. urtean, optikari buruzko idatzirik garrantzitsuena argitaratu zuen, Optiks, non bere aurreko teoria guztiak eta argiaren natura korpuskulua azaltzen zuen. Baita errefrakzio, islapen, eta argiaren sakabanatzea garatu zuen.
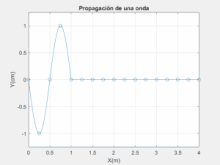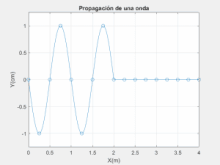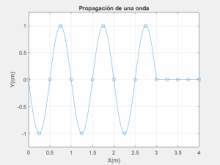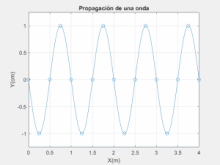
Argiaren natura korpuskularraren ideiak deuseztatu arren, gaur egun zientzialariak adostu dute argia bi modutan sakabanatzen dela: korpuskulu eta uhin moduan. Honetan oinarritzen da mekanika kuantikoa.
Grabitazio unibertsalaren legea
1686an, Isaac Newtonek bi partikularen arteko erakarpen-indar grabitatorioaren adierazpen matematikoa formulatu zuen; hala, grabitazio unibertsalaren legea enuntziatu zuen.
Unibertsoko bi partikula materialek elkar erakartzen dute, haien masen biderkadurarekiko zuzenki proportzionala eta haien arteko distantziaren karratuarekiko alderantziz proportzionala den indarrarekin.
Adierazpen horretatik, ondorio hauek atera ditzakegu:
- Bi gorputzen arteko erakarpen-indar grabitatorioa eragiten duen propietatea gorputzen masa da.
- Adierazpen matematikoak ikur negatiboa du, grabitate-indarrak eta bektore unitarioak aurkako noranzkoa dutelako; hau da, grabitate indarra erakarpenezkoa delako.
- Proportzionaltasun-konstante edo grabitazio unibertsalaren konstante (G) deritzonak balio berbera du unibertsoko edozein lekutan. Newtonek legea enuntziatu zenetik mende batera, Henry Cavendish-ek konstante horren balioa neurtu zuen, tortsio-balantza batekin. Gaur egun, konstantearen balioa 6,67·10-11N·m2·kg-2 dela jotzen da.
- G konstantearen balioa oso txikia denez, masa txikiko gorputzek erakarpen-indar grabitatorio txikia egiten diote elkarri, eta masa handiko gorputzek (planetak, sateliteak...), berriz, handia.
Legearen historia
Grabitazio unibertsalaren legea 1685. urtean bukatu zuen, aurretik hasitako ikasketa eta lanen ondorioz. 1551. urtean Domingo de Soto, zientzialari espainiarra, lehenengoa izan zen esaten gorputz batek erorketa askean azelerazio konstante bat izaten zuela. Lehenengo erreferentzia idatzia Robert Hooke-ek idatzi zuen 1666. urtean, Micrographia liburuan. 13 urte geroago, Newtonek erlazionatu zuen probleman ibilbide kurbo batean neurtzekotan. Robertek Royal Society-ko idazkariaren postua lortzean, filosofiari buruzko karten bidez hitz egiten hasi zen Newtonekin, non lehenengo bietan Newtonen intereseko bi gai aztertu zituen. Momentuz, garai hori baino lehen, Descartes eta Huygens izan ziren bakarrak kurbadun mugimendua indar zentrifugoaren bidez hitz egiten filosofo eta zientzialari bakarrak; baina Hooke, modu berri bat proposatu zuen hori kalkulatzeko, tangentearen bidez. Proposamen horretan eguzkia, tangentea eta indar zentripetua erlazionatzen du; hala ere, Isaac Newton ez zuen inoiz entzun horrelako hipotesirik.
Beste gutun batean Hooker-ek esaten du: “Orain lerro kurba bateko propietateak entzun behar ditugu, distantzia guztiei alderantzizko proportzio koadratikoa neurtuz”. Beste moduan esanda, jakin nahi zuen zein da objektu baten kurba erresultantea aplikatu zaion alderantzizko indarra distantziarekiko karratua. Azkeneko esaldia izan zen: “Argi daukat zure ebazpen ikaragarriarekin aurki dezakezu zein izan behar den kurba hori”.
1684an, Newtonek Edmun Halley-ri jakinarazi zion indarraren problemari erantzun bat aurkitu ziola. Newtonek De Motu tratatuan idatzi zituen kalkulu horiek eta Philosophiae naturalis principia mathematica liburuan ederki zabaldu eta azaldu zituen teoria, kalkulu eta metodo guztiak. Hori hobe egiteko, Kepler-ren legeak erabili zituen, zein oso gutxi erabiliak zeuden garai horretako zientzialarietatik.
Ondorioa
Hori dela eta, esan dezakegu grabitazio unibertsalaren legea ez dela bakarrik eguzkiraino doan indar batean. Planeten efektu bat eguzkiarekiko eta Unibertsoko objektu guztietara doala ere. Efektu hori dinamikaren hirugarren legean azalduta dago; kasu horretan, objektu bat bigarren objektu bat erakartzen badu, bigarrenak ere lehenengoa erakartzen du indar berdinarekin.
Beste ondorioztapen bat izan zen, planeten mugimendua ezin izan zela erregularra. Esan zuen: “planetak ez dira elipseetan zehazki mugitzen, ezta ezin dute biratu bi alditan orbita berdinera.” Teoria hauengatik zailagoa egiten zuten bere sinesmen erlijiosoak aurrera eramatea, indar dibinoa deuseztatzen zutelako.
Newtonen dinamikaren legeak
Dinamikak azaltzen du zerk eragiten duen higidura, eta hiru legeak arautzen dute. Newton-ek ezarri zituen dinamikaren oinarriak, 1687an, Fillosofia naturalaren printzipio matematikoak izeneko lanean. Hiru legeei Newtonen legeak deritze. Dinamikaren legeek erabateko baliagarritasuna dute erreferentzia-sistema inertzialetan: guztiz ondo azaltzen dute edozein objekturen higidura, betiere behatzailea geldiunean badago, edo lerro zuzenean eta abiadura konstantean higitzen bada behatzailea.
Erreferentzia-sistema bat geldiunean badago, edo lerro zuzenean eta abiadura konstantean higitzen bada, orduan, erreferentzia-sistema inertziala da. Gainerako unibertsoarekin elkarrekintzarik ez daukan sistematzat har dezakegu.
Newtonen lehen legea
Newtonen lehen legeari inertziaren legea ere baderitzo. Esperientziak esaten digunez, geldiunean dagoen objektua higiduran jartzeko, indarren bat aplikatu behar diogu, eta, halaber, objektua abiadura konstantean higitzen bada, indarra aplikatu behar zaio geldiarazteko.
Inertzia da gorputz orok geldiunean irauteko edo higidura zuzen uniformea mantentzeko duen joera.
Gorputz ororen geldiuneko egoerak edo higidura zuzen uniformeak bere horretan dirau gorputzaren gainean indar garbirik edo erresultanterik ez dagoen bitartean.
Ez dago egiterik lege horren egiaztapen esperimental zuzenik, postulatutzat enuntziatua izan delako. Lege hori da behaketaren eta esperientziaren abstrakzioa eginez lortutako idealizazioa. Kontua da ez dela existitzen gorputz errealik besteen eraginik edo ingurunearen eraginik ez daukanik. Esaterako, HZUan dagoen gorputzak ezin du bere horretan jarraitu baldin eta ez badago higidurari aurre egiten dioten marruskadura-indarrak konpentsatzeko beste indarrik.
Newtonen bigarren legea
Lege honi, halaber, dinamikaren oinarrizko legea deritzo, eta deskribatzen du gorputz bati zer gertatzen zaion indar garbi batek eragiten dionean. Ulertzeko, magnitude fisiko berri bat erabili behar da: momentu lineala.
Momentu lineala
Gorputz baten masa eta ―geldiarazteko zailtasunaren maila, beraz― aintzakotzat hartzen duen magnitude fisikoari momentu lineal edo higidura kantitate deritzo:
Gorputz baten momentu lineala magnitude bektoriala da. Gorputzaren masarekiko eta abiadurarekiko zuzenki proportzionala da.
Definizio horren arabera, m masako eta abiaduran higitzen den gorputzaren momentu lineala honela kalkulatzen da: .
Momentu linealaren eta abiaduraren norabideak eta noranzkoak berdinak dira: higidurarekiko ukitzaile. Momentu linealaren unitateak -1 dira, SIn.
Newtonen bigarren legearen enuntziatua
Enuntziatuaren arabera, m masako gorputzari eragiten dion indarrak gorputzaren momentu linealaren aldaketa eragingo du, denborarekiko.
Edozein gorputzi eragiten dion indar orok (garbi edo erresultante) gorputzaren momentu linealaren aldaketa eragingo du, denboran.
Lege honen adierazpen matematikoa hau da:
Adierazpen horretan onartu dugu gorputzaren masa konstantea dela.
- Newton (N) unitatea da 1 kg-eko masadun gorputzari 1 -2-ko azelerazioa eragiten dion indarra.
- Gorputza, geldiunetik abiatuta, higidura zuzen uniformeki azeleratuarekin higituko da, eragiten dion indar erresultantearen norabidean eta noranzkoan.
Newtonen hirugarren legea
Newtonen hirugarren legea, edo akzioaren eta erreakzioaren legea, bi gorputzen arteko elkarrekintzei dagokie, eta honela adierazten da:
A gorputzak B gorputzari indar bat (akzio deritzoguna) eragiten dionean, B gorputzak erantzuten du A gorputzari balio bereko baina kontrako noranzkoko indarra (erreakzio deritzona) eraginez.
- Akzioaren eta erreakzioaren legearen arabera, indarrek, elkarrekintza baten ondoriozkoak haiek, bikoteka eragiten dute beti.
- Akzio-indarra eta erreakzio-indarra aldi berean agertzen dira, baina ez dute elkar deuseztatzen, objektu desberdinei aplikatzen baitzaizkie akzio-indarra eta erreakzio-indarra; horrexegatik sorrarazten dituzte efektu desberdinak.
- Newtonen hirugarren legeak ohiko gertakariak azaltzen ditu: zergatik higitzen garen ibiltzean, hegazkinek edo suziriek zergatik egin dezaketen aurrera, horma baten kontra jaurtitako pilotak zergatik errebotatzen duen eta abar.
Ekimen publikoa
1687. urtean Cambridgeko Unibertsitateko eskubideak defendatu zituen Jacobo II. erregearen kontra joanez, sortu nahi zuelako leku katoliko bat unibertsitatearen lekuan. Gertaera horri esker Parlamentuko kidea aukeratu zuten 1689. urtean erregeari postua kendu ziotenean. Bere postua izan zuen urte batzuetan, baina eztabaidetan ez zuen parterik hartzen. Denbora horretan bere kimikako ikasketak jarraitu zituen. Baita hidrostatika eta hidrodinamikako ikerketak jarraitu zituen, eta teleskopioak sortzen jarraitu zuen.
30 urteetan zehar irakaslea izan zen, eta bere postua utzi zuen Txanponaren Etxeko zuzendariaren postua onartuz 1696. urtean. Denbora horretan jende asko bidali zuen urkamendira billeteak faltsuak ekoizteagatik. Bere bizitzaren azkeneko 30 urteetan zientziari uko egin zion eta ikasketa erlijiosoak hasi zituen. Royal Society-ko lehendakaria aukeratu zuten 1703. urtean eta berraukeratu zuten urtero hil arte. 1705. urtean Ana erregina zalduna izendatu zuen Ingalaterrari emandako zerbitzuengatik.
Alkimia
Alkimiari buruzko milioi bat hitz baino gehiago idatzi zituen, baina oso berandu jakin izan zen, ilegala zelako garai horretan. Newtonek lanak sinatu zituen Jeova Sanctus Unus esaldiarekin, trinitarioen kontrako goiburu bat dena: Jeova, santu bakarra, eta baita Isaac Newtonen izen latinizatuaren anagrama bat dena (Isaacus Neuutonus-Ieova Sanctus Unus). Bere gelaren atzeko lorategian, estalpe bat eraiki zuen laborategi moduan, non sua beti piztuta zegoela eta alkimiako esperimentuak egin zituen.
Alkimiaren munduan sartu baino lehen, Isaac Barrow eta Henry More ezagutu zituen, Cambridgeko intelektualak. 1669. urtean alkimiako lehen bi lanak egin zituen: Theatrum Chemicum eta The Vegetation of Metals. Urte berean, Cambridgeko irakasle Lucasiarra izendatu zuten.
1680. urtean, bere idazlan luzeena idatzi zuen, alkimiari buruzkoa. Index Chemicus deitzen zen eta nabarmena zen antolaketa eta sintesi lan handia egin zuelako; mende bukaeran bukatu zuen. Ere bai, 1692an bi entsegu idatzi zituen, De Natura Acidorum nagusiena dena, non azidoen akzio kimikoa ikertzen du, molekulen indar erakarpenaren bidez. Oso interesgarria da ikustea nola erlazionatzen du alkimia indarren hizkuntza fisikoarekin.
Hurrengo mendean bere lan alkimikoak jarraitu zituen Ripley Expounded, Tabula Smaragdina eta Praxis lana idazten.
Aipatu behar da Newtonek txikitatik ez zela fidatzen medikuntza ofizialetik eta bere ezagutzak erabiltzen zituen bere kabuz sendagaiak hartzeko. Historialari askok esaten zuten sendagai alkimikoak pozoitsuak zirela eta arazo asko sortu zituztela. Hala ere, 84 urte bizi zituen.
Teologia
Bere bizitza osoan oso gizon erlijiosoa izan zen. Bere gurasoak puritanoak ziren, eta egon zen denbora gehiago Biblia ikasten zientzia baino. Analisi batek esaten du Newtonek idatzitako 3.600.000 hitzetatik, bakarrik milioi bat zientziari buruzkoak zirela, eta 1.400.000 teologiari buruzkoak. Baita ere ezagutzen da 19 urterekin idatzi zituela 58 bekatuen zerrenda bat. Horretako bat hau da: “Nire aita eta ama mehatxatu, haiek haien etxearekin su piztuz”.
Newtonek jainko bakar batean sinisten zuen, Aita Jainkoarekin. Bere ikasketa teologikoak alkimiakoekin erlazionatu zituen eta ere uste zuen Moises alkimista bat izan zela. Bere ideologia antitrinitarioa buruhauste asko sortu zitzaion, Cambridgeko Trinity Collegen ikasten zuenez eta Santa Trinitatearen ideologia jarraitu behar zuelako. Londresera bidai bat egin zuen Carlos II.ari eskatzeko ordre sakratuak emateko, eta eman zitzaizkion.
Cambridgera bueltatu zenean, John Locke filosofoarekin gutunak elkarri bidaltzen hasi zen. Konfiantza nahikoa izan zuen Trinitateari buruzko iritzia emateko, eta filosofoa esan zion haren idazpen teologikoak jarraitzeko. Idatzi teologiko nabarmenenak hauek dira: An Historical Account of Two Notable Corruption of Scriptures, Chronology of Ancient Kingdoms Atended eta Observations upon the Prophecies. Baita ere azken auziko eguna kalkulatu zuen, eta esan zuen 2060. urtetik baino lehen izango zela.
Bere garaiako beste zientzialariekin izandako harremana
Isaac Newtonek 1687. urtean Filosofia naturaleko oinarrizko matematikako liburuak argitaratu zituen. Robert Hooke-rren “Micrographia” liburua 22 urte aurretik argitaratu zen eta biak mugimenduko eta grabitatearen legeak azaltzen zituen, baina Allan Chapman esaten duen bezala, Hooke Newton baino lehenago idatzi zuen grabitatearen teoriak. Hooke-rren lanak eragin zuten Newtonek argiaren naturari buruz ikastea.
Bi zientzialariak gatazkak izan zituzten optika eta grabitazioari buruzko legeei buruz. Newtonek Principios liburutik Hookerri buruzko erreferentzia guztiak kendu zituen. Historialari bat esan du Newtonek saiatu dela Hookerri buruzko lan, tresna, asmakizun eta teoria guztiak ezabatzea, eta parte batean lortu zuen Royal Society-ko lehendakaria bihurtzean.
Azkeneko urteak
Bere azkeneko urteak ez ziren hoberenak izan, Leibniz-ekin izandako gatazketatik, analisi berri batek sortzean. Elkarri egindako kopiaketa akusazioak, kriptogrametan disimulatutako sekretuak, egile ezezaguneko gutunak, argitaragabeko tratatuak eta beste arazo askoren ondoren, Leibniz hil zen 1716. urtean.
Isaac Newton begirune handiz tratatua izan da bere bizitza osoan, beste zientzialariak ez bezala, eta honen froga, izan zituen karguak dira: 1689. urtean, parlamentuko kide aukeratu zuten; 1696an, Txanponaren Etxeko zuzendaria; 1703an, Royal Society-ko lehendakaria eta 1705. urtean, Ana erreginarengandik Sir izena jaso zuen.
Zaharra izan zenean, giltzurrunetako arazo asko jasan zituen; gehienak, koliko nefritikoak izan ziren, eta honetako batengatik hil zen 1727ko martxoaren 31an, eramankizun askoren ondoren. Gorpuzkiak, Westminsterreko abadian dauden, Ingalaterrako beste jaun askoren ondoan.
Newtonen obra handia Nicolás Copérnico hasitako zientzia iraultzari bukaera eman zion, eta arrazoian oinarritutako konfiantza garai bat hasi zuen, ezagutzaren arlo guztietara zabaltzen zena.
Eponimoa
- Newtonen kanoi bola: hau, Newtonek izandako esperimentu mental bat izan zen, eta honekin hipotesi bat egin zuen munduko grabitatea unibertsala zela ziurtatzeko.
- Newtonen hodia: zilindro itxurako hodi gardena, haren barnean hutsa eginez, gorputz guztiek, duten dentsitatea dutela, lastertasun beraz erortzen direla frogatzeko erabiltzen dena.
- Newtonen hozte legea: gorputzak nola hozten diren adierazten duen legea. Lege honen arabera, gorputz batek beroa gorputzaren eta ingurunearen artean den bero diferentziari buruzko proportzioan galtzen du; lege enpirikoa den arren, errazago betetzen da tenperatura diferentziak txikiak direnean; tenperatura diferentziak handiak direnean, berriz, beroa konbekzioz galtzen denean betetzen da soilik[2].
- Newtonen jariakina: Newton-en likatasunaren legea betetzen duen jariakina; lege honen arabera, jariakin jakin baten bi geruza lerrokideen artean den indar tangentziala jaraikinen geruzen azaleraren, bi geruzen arteko distantziaren, haien abiaduraren eta likatasun-koefizientearen funtzioa da.
- Newtonen teleskopioa: ardatzak elkarzut dituzten ispilu ganbil batez eta okular batez osatua dagoen erreflexio teleskopioa. Ispilu ganbilak objektiboaren eginkizuna du. Ispiluaren ardatzean horizontalarekin 45°tako angelua osatzen duen ispilu lau bat izaten da[3].
- Newtonen identitateak: matematiketan, polinomioen erroak deskribatzeko modu ezberdinak dira. Newton-Girard formulak ere dei ditzakegu.
- Newtonen eraztunak: Optics lanean Newtonek deskribatzen zuen esperientzia batean, foku distantzia handia zuen lente lau-ganbil baten alde ganbila beirazko azalera lau baten gainean jartzen zuen. Aire geruzak islatzen zuen argian lentearen eta beiraren ukimen puntuarekiko kontzentrikoak ziren kolorezko eraztun batzuk ikusten zituen. Eraztunen diametroa bi kristalen arteko distantziaren arabera aldatzen zen. Horiek dira Newtonen eraztunak. Eraztun horiei buruzko legeak formulatu zituen. Eraztunak argi interferentziei esker eratzen dira, baina ez zuen hala uste izan Newtonek eta gorputzen teoria baieztatzen aurrera egin zuen.
- Newtonen diskoa: Eremu koloreztatuetan zatikatutako kartoizko diskoa. Bertan argi zuriaren osagai diren koloreak daude margotuta: gorria, laranja, horia, berdea, urdina, anila eta morea. Diskoa lastertasun handiz biraraziz gero, zuriz koloreztatua dagoela dirudi[4].
- Newtonen legeak: Newtonen legeak gorputzen higidura azaltzeko erabiltzen diren hiru printzipio dira. Lege hauen formulazio matematikoa Isaac Newtonek argitaratu zuen 1687. urtean, bere Philosophiæ Naturalis Principia Mathematica liburuan. Newtonen legeak, Galileoren transformazioekin batera, mekanika klasikoaren oinarria dira.
- Newtonen metala: metal hau aleazio bat da, zeinen fusio puntua oso baxua dela. Haren konposizioaren % 50 bismutoa da, % 31,2 burdina eta %18,8 eztainua.
- Newton (unitatea): Fisikan, newton (N) bat, indarraren unitatea da Nazioarteko Unitate Sisteman, Isaac Newton-en omenez jarri zioten izena. Kilogramo bateko objektu bat 1 m/s²-ko azelerazio batera iristeko behar den indarra bezala definitzen da.
- Newtonen metodoa: funtzio erreal baten 0 edo erroen hurbilera aurkitzeko algoritmo bat da.
Newtonen obra idatzia
- Method of Fluxions (1671, 1736. urtean argitaratuta)
- Of Natures Obvious Laws & Processes in Vegetation (1671-75, ez dute argitaratu)
- De motu corporum in gyrum (1684)
- Philosophiae naturalis principia mathematica (1687) (The Principia: Mathematical Principles of Natural Philosophy. University of California Press, (1999).
- Opticks (1704)
- Reports as Master of the Mint (1701-25)
- Arithmetica universalis (1707)
Hil ondoren argitaratutako idatziak
- The System of the World, Optical Lectures, The Chronology of Ancient Kingdoms, and De mundi systemate 1728 (Lurraren sistema, irakurmen optikoak, erreinu antzinen kronologia eta sistema mundiala).
- Observations on Daniel and The Apocalypse of St. John . (Daniel eta San Juanen apokalipsiaren profezien gaineko obserbazioak).
- An Historical Account of Two Notable Corruptions of Scripture 1754 (Bi idatzi ustel nabarmenen erlazio historikoa).
Erreferentziak
- Artikulu honen edukiaren zati bat Lur hiztegi entziklopedikotik edo Lur entziklopedia tematikotik txertatu zen 2011/12/26 egunean. Egile-eskubideen jabeak, Eusko Jaurlaritzak, hiztegi horiek CC-BY 3.0 lizentziarekin argitaratu ditu, Open Data Euskadi webgunean.
- (Gaztelaniaz) «Isaac Newton, científico y alquimista» historia.nationalgeographic.com.es 2016-03-31 (Noiz kontsultatua: 2022-12-12).
- «Ley del enfriamiento de Newton» www.sc.ehu.es (Noiz kontsultatua: 2021-02-15).
- (Gaztelaniaz) Telescopio newtoniano. 2020-05-11 (Noiz kontsultatua: 2021-02-15).
- (Gaztelaniaz) Disco de Newton. 2021-01-28 (Noiz kontsultatua: 2021-02-15).
Kanpo estekak
| Wikimedia Commonsen badira fitxategi gehiago, gai hau dutenak: Isaac Newton |
| Wikiesanetan badira aipuak, gai hau dutenak: Isaac Newton |